11.2: Simple Harmonic Motion
- Page ID
- 22268
A particularly important kind of oscillatory motion is called simple harmonic motion. This is what happens when the restoring force is linear in the displacement from the equilibrium position: that is to say, in one dimension, if \(x_0\) is the equilibrium position, the restoring force has the form
\[ F=-k\left(x-x_{0}\right) \label{eq:11.2} .\]
We are familiar with this from Hooke’s “law” for an ideal spring (see Chapter 6). So, an object attached to an ideal, massless spring, as in the figure below, should perform simple harmonic motion. This kind of oscillation is distinguished by the following characteristics:
- The position as a function of time, \(x(t)\), is a sinusoidal function.
- The period of the oscillations does not depend on their amplitude (by “amplitude” we mean the maximum displacement from the equilibrium position).
What this second property means is that, for instance, with reference to Figure \(\PageIndex{1}\), you can displace the mass a distance \(A\), or \(A/2\), or \(A/3\), or whatever you choose, and the period (and frequency) of the resulting oscillations will be the same regardless. (This means, actually, that if you displace it farther it has to end up moving faster, to cover the larger distance in the same time.)
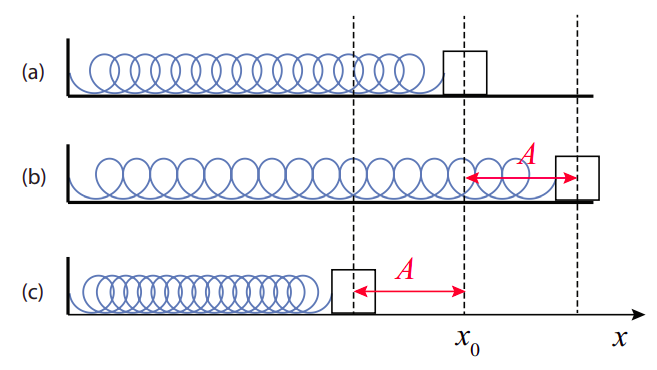
Since we know that “Hooke’s law” is actually just an approximation, valid only provided that the spring is not compressed or stretched too much, we expect that in real life the “ideal” simple harmonic motion properties I have listed above will only hold approximately, as well; so, in fact, if you stretch a spring too much you will get a different period, eventually, than if you stay in the “linear,” Hooke’s law regime. This is a general characteristic of most physical systems: simple harmonic motion only happens for relatively small oscillations, but “relatively small” can still be fairly large sometimes, and even as an approximation it is often an extremely valuable one.
The other distinctive characteristic of simple harmonic motion is that the position function is sinusoidal, by which I mean a sine or a cosine. Thus, for example, if the mass in Figure \(\PageIndex{1}\) is released from rest at \(t\) = 0, and the position \(x\) is measured from the equilibrium position \(x_0\) (that is, the point \(x = x_0\) is taken as the origin of coordinates), the function \(x(t)\) will be
\[ x(t)=A \cos (\omega t) \label{eq:11.3} \]
where the quantity \(\omega\), known as the oscillator’s angular frequency, is given by
\[ \omega=\sqrt{\frac{k}{m}} \label{eq:11.4} .\]
Here, \(k\) is the spring constant, and \(m\) the mass of the object (remember the spring is assumed to be massless). I will prove that Equation (\ref{eq:11.3}), together with (\ref{eq:11.4}), satisfy Newton’s second law of motion for this system in a moment; first, however, I need to say a couple of things about \(\omega\). You’ll recall that we have used this symbol before, in Chapter 9, to represent the angular velocity of a particle moving in a circle (or, more generally, of any rotating object). Why bring it up again now for an apparently completely different purpose?
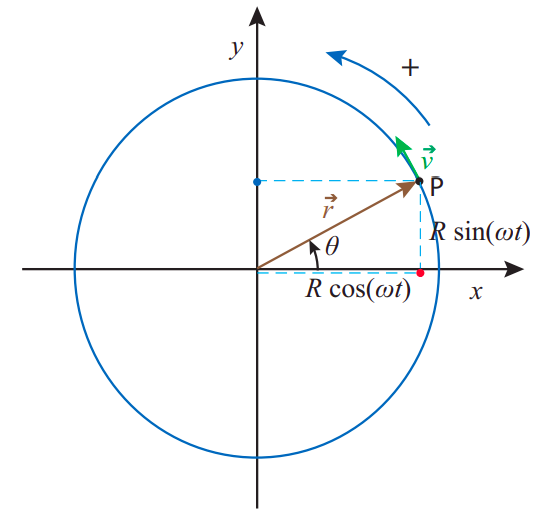
The answer is that there is a very close relationship between simple harmonic motion and circular motion with constant speed, as Figure \(\PageIndex{2}\) illustrates: as the point P rotates with constant angular velocity \(\omega\), its projection onto the \(x\) axis (the red dot in the figure) performs simple harmonic motion with angular frequency \(\omega\) (and amplitude \(R\)). (Of course, there is nothing special about the \(x\) axis; the projection on any other axis will also perform simple harmonic motion with the same angular frequency; for example, the blue dot on the figure.)
If the angular velocity of the particle in Figure \(\PageIndex{2}\) is constant, then its “orbital period” (the time needed to complete one revolution) will be \(T = 2\pi/\omega\), and this will also be the period of the associated harmonic motion (the time it takes for the motion to repeat itself). You can see this directly from Equation (\ref{eq:11.3}): if you increase the time \(t\) by \(2\pi/\omega\), you get the same value of \(x\):
\[ x\left(t+\frac{2 \pi}{\omega}\right)=A \cos \left[\omega\left(t+\frac{2 \pi}{\omega}\right)\right]=A \cos (\omega t+2 \pi)=A \cos (\omega t)=x(t) \label{eq:11.5} .\]
Since the frequency \(f\) of an oscillator is equal to 1/\(T\), this gives us the following relationship between \(f\) and \(\omega\):
\[ f=\frac{1}{T}=\frac{\omega}{2 \pi} \label{eq:11.6} .\]
One way to tell whether one is talking about an oscillator’s frequency (\(f\)) or its angular frequency (\(\omega\))—apart from the different symbols, of course—is to pay attention to the units. The frequency \(f\) is usually given in hertz, whereas the angular frequency \(\omega\) is always given in radians per second. Apart from the factor of \(2\pi\), they are, of course, completely equivalent; sometimes one is just more convenient than the other. On the other hand, the only way to tell whether \(\omega\) is a harmonic oscillator’s angular frequency or the angular velocity of something moving in a circle is from the context. (In this chapter, of course, it will always be the former).
Let us go back now to Equation \ref{eq:11.3} for our block-on-a-spring system. The derivative with respect to time will give us the block’s velocity. This is a simple application of the chain rule of calculus:
\[ v(t)=\frac{d x}{d t}=-\omega A \sin (\omega t) \label{eq:11.7} .\]
Another derivative will then give us the acceleration:
\[ a(t)=\frac{d v}{d t}=-\omega^{2} A \cos (\omega t) \label{eq:11.8} .\]
Note that the acceleration is always proportional to the position, only with the opposite sign. The proportionality constant is \(\omega^2\). Since the force exerted by the spring on the block is \(F = −kx\) (because we are measuring the position from the equilibrium position \(x_0\)), Newton’s second law, \(F = ma\), gives us
\[ ma = -kx \label{eq:11.9} \]
and you can check for yourself that this will be satisfied if \(x\) is given by Equation (\ref{eq:11.3}), \(a\) is given by Equation (\ref{eq:11.8}), and \(\omega\) is given by Equation (\ref{eq:11.4}).
The expression (\ref{eq:11.4}) for \(\omega\) is typical of what we find for many different kinds of oscillators: the restoring force (here represented by the spring constant \(k\)) and the object’s inertia (\(m\)) together determine the frequency of the motion, acting in opposite directions: a larger restoring force means a higher frequency (faster oscillations) whereas a larger inertia means a lower frequency (slower oscillations—a more “sluggish” response).
The position, velocity and acceleration graphs for the motion (\ref{eq:11.3}) are shown in Figure \(\PageIndex{3}\) below. You may want to pay attention to some of their main features. For instance, the position and the velocity are what we call “90\(^{\circ}\) out of phase”: one is maximum (or minimum) when the other one is zero. The acceleration, on the other hand, is “180\(^{\circ}\) out of phase” (that is to say, in complete opposition) with the position. As a result of that, all combinations of signs for \(a\) and \(v\) are possible: the object may be moving to the right with positive or negative acceleration (depending on which side of the origin it’s on), and likewise when it is moving to the left.
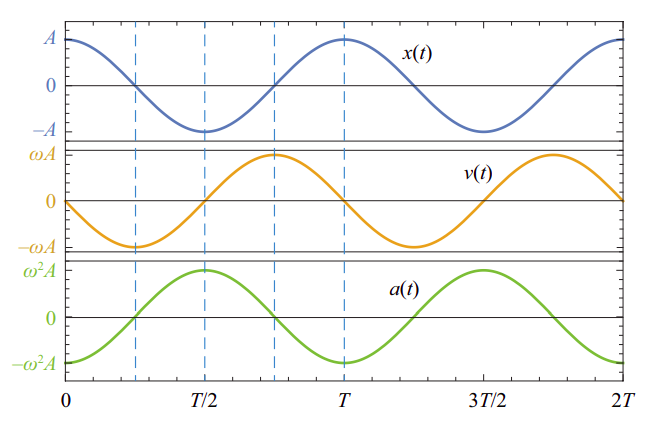
Since the time we choose as \(t\) = 0 is arbitrary, the function in Equation (\ref{eq:11.3}) (which assumes that \(t\) = 0 is when the object’s displacement is maximum and positive) is clearly not the most general formula for simple harmonic motion. Another way to see this is to realize that we could have started the motion differently. For instance, we could have hit the block with a sharp, “impulsive” force, lasting only a very short time, so it would have acquired a substantial velocity before it could have moved very far from its initial (equilibrium) position. In such a case, the motion would be better described by a sine function, such as \(x(t) = A \sin(\omega t)\), which is zero at \(t\) = 0 but whose derivative (the object’s velocity) is maximum at that time.
If we stick to using cosines, for definiteness, then the most general equation for the position of a simple harmonic oscillator is as follows:
\[ x(t)=A \cos (\omega t+\phi) \label{eq:11.10} \]
where \(\phi\) is what we call a “phase angle,” that allows us to match the function to the initial conditions—by which I mean, the object’s initial position and velocity. Specifically, you can see, by setting \(t\) = 0 in Equation (\ref{eq:11.10}) and its derivative, that the initial position and velocity of the motion described by Equation (\ref{eq:11.10}) are
\begin{align}
x_{i}&=A \cos \phi \nonumber \\
v_{i}&=-\omega A \sin \phi \label{eq:11.11}.
\end{align}
Conversely, if you are given \(x_i\) and \(v_i\), you can use Eqs. (\ref{eq:11.11}) to determine \(A\) and \(\phi\), which is what you need to know in order to use Equation (\ref{eq:11.10}) (note that the angular frequency, \(\omega\), does not depend on the initial conditions—it is always the same regardless of how you choose to start the motion). Specifically, you can verify that Eqs. (\ref{eq:11.11}) imply the following:
\[ A^{2}=x_{i}^{2}+\frac{v_{i}^{2}}{\omega^{2}} \label{eq:11.12} \]
and then, once you know \(A\), you can get \(\phi\) from either \(x_i = A \cos \phi\) or \(v_i = −\omega A \sin \phi\) (in fact, since the inverse sine and inverse cosine are both multivalued functions, you should use both equations, to make sure you get the correct sign for \(\phi\)).
Energy in Simple Harmonic Motion
Equation (\ref{eq:11.11}) above actually follows from the conservation of energy principle for a harmonic oscillator. Consider again the mass on the spring in Figure \(\PageIndex{2}\). Its kinetic energy is clearly \(K = \frac{1}{2}mv^2\), whereas the potential energy in the spring is \(\frac{1}{2}kx^2\). Using Equation (\ref{eq:11.10}) and its derivative, we have
\begin{align}
U^{s p r} &=\frac{1}{2} k A^{2} \cos ^{2}(\omega t+\phi) \nonumber \\
K &=\frac{1}{2} m \omega^{2} A^{2} \sin ^{2}(\omega t+\phi) \label{eq:11.13}.
\end{align}
Recalling Equation (\ref{eq:11.4}), note that \(\omega^2 = k/m\), so if you substitute this in the second equation above, you can see that the amplitude of both the potential and the kinetic energy is the same, namely, \(\frac{1}{2}kA^2\). Since, for any angle \(\theta\), it is always true that \(\cos^2 \theta + \sin^2 \theta = 1\), we find
\[ E_{s y s}=U^{s p r}+K=\frac{1}{2} k A^{2}=\frac{1}{2} m \omega^{2} A^{2} \label{eq:11.14} \]
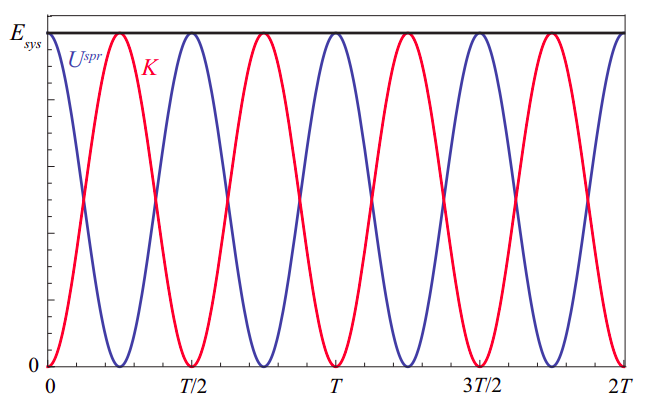
so the total energy of the system is constant (independent of time), at it should be, in the absence of dissipation. Figure \(\PageIndex{4}\) shows how the potential and kinetic energies oscillate in opposition, so one is maximum whenever the other is minimum. It also shows that they oscillate twice as fast as the oscillator itself: for example, the potential energy is maximum both when the displacement is maximum (spring maximally stretched) and when it is minimum (spring maximally compressed). Similarly, the kinetic energy is maximum when the oscillator passes through the equilibrium position, regardless of whether it is moving to the left or to the right.
Harmonic Oscillator Subject to an External, Constant Force
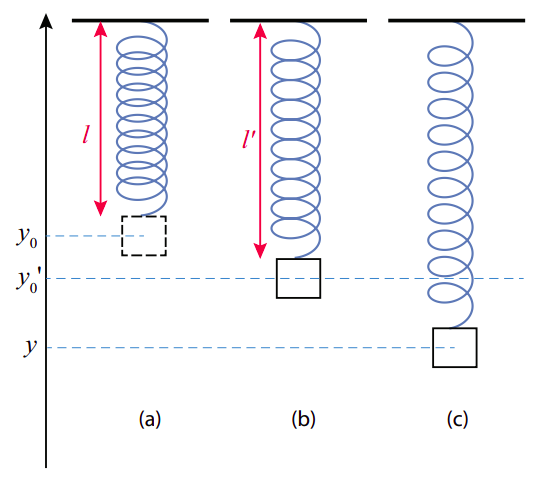
Consider a mass hanging from an ideal spring suspended from the ceiling, as in Figure \(\PageIndex{5}\) below (next page). Supposed the relaxed length of the spring is \(l\), such that, in the absence of gravity, the object’s equilibrium position would be at the height \(y_0\) shown in figure \(\PageIndex{5}\)(a). In the presence of gravity, of course, the spring needs to stretch, to balance the object’s weight, and so the actual equilibrium position for the system will be \(y^{\prime}_0\), as shown in figure \(\PageIndex{5}\)(b). The upwards force from the spring at that point will be \(-k\left(y_{0}^{\prime}-y_{0}\right)\), and to balance gravity we must have
\[ -k\left(y_{0}^{\prime}-y_{0}\right)-m g=0 \label{eq:11.15} .\]
Suppose that we now stretch the spring beyond this new equilibrium position, so the mass is now at a height \(y\) (figure \(\PageIndex{5}\)(c)). What happens then? The net upwards force will be \(-k\left(y-y_{0}\right)-m g\), but using Equation (\ref{eq:11.15}) this can be rewritten as
\[ F_{n e t}=-k\left(y-y_{0}\right)-m g=-k\left(y-y_{0}^{\prime}\right)--k\left(y_{0}^{\prime}-y_{0}\right)-m g=-k\left(y-y_{0}^{\prime}\right) \label{eq:11.16} .\]
This is a remarkable result, because the force of gravity has disappeared completely from the final expression. Basically, the system behaves as if it consisted of just a spring of constant \(k\) with equilibrium length \(l^{\prime}=l+y_{0}-y_{0}^{\prime}\), and no gravity. In other words, the only thing gravity does is to change the equilibrium position, so that if you now displace the mass, it will oscillate around \(y_{0}^{\prime}\) instead of around \(y_0\). The oscillation’s period and frequency are the same as if the spring was horizontal.
Although I have established this here for the specific case where the oscillator involves a spring, and the external force is gravity, this is a completely general result, valid for any simple harmonic oscillator, since for such a system the restoring force will always be a linear function of the displacement (which is all that is required for the math to work). As long as the external force is constant, the frequency of the oscillations will not be affected, and only the equilibrium position will change. In an example at the end of the chapter (under “Advanced Topics”) I will show you how you can make use of this to calculate the effect of friction on the horizontal mass-spring combination in Figure \(\PageIndex{1}\).
One thing you need to keep in mind, however, is that when the oscillator is subjected to an external force, as was the case here, its energy will not, in general, remain constant (unlike what we saw in the previous subsection "Energy in Simple Harmonic Motion"), since the external force will be doing work on the system as it oscillates. If the external force is constant, and does not change direction, this work will be positive half the time, and negative half the time. If it is kinetic friction, then of course it will change direction every half cycle, and the work will be negative all the time.
In the case shown in Figure \(\PageIndex{5}\), the external force is gravity, which we know to be a conservative force, so the energy that will be conserved will be the total energy of the system that includes the oscillation and the Earth, and hence also the gravitational potential energy (for which we can use here the familiar form \(U^G = mgy\)):
\[ E_{\text {osc+earth }}=U^{s p r}+K+U^{G}=\frac{1}{2}\left(y-y_{0}\right)^{2}+\frac{1}{2} m v^{2}+m g y=\text { const } \label{eq:11.17} .\]
The reason it is no longer possible to combine the terms \(U^{spr} + K\) into the constant \(\frac{1}{2} kA^2\), as in Equation (\ref{eq:11.14}), is that now we have
\begin{align}
&y(t)=y_{0}^{\prime}+A \cos (\omega t+\phi) \nonumber \\
&v(t)=-\omega A \sin (\omega t+\phi) \label{eq:11.18}
\end{align}
so the oscillations are centered around the new equilibrium position \(y_{0}^{\prime}\), but the spring energy is not zero at that point: it is zero at \(y = y_0\) instead. You can check for yourself, however, that if you substitute Eqs. (\ref{eq:11.18}) into Equation (\ref{eq:11.17}), and make use of the fact that \(k\left(y_{0}^{\prime}-y_{0}\right)=-m g\) (Equation (\ref{eq:11.15})), you do indeed get a constant, as you should.


