12.1: Traveling Waves
- Page ID
- 22274
In our study of mechanics we have so far dealt with particle-like objects (objects that have only translational energy), and extended, rigid objects, which may also have rotational energy. We have, however, implicitly assumed that all the objects we studied had some internal structure, or were to some extent deformable, whenever we allowed for the possibility of their storing other forms of energy, such as chemical or thermal.
This chapter deals with a very common type of organized (as opposed to incoherent) motion exhibited by extended elastic objects, namely, wave motion. (Often, the “object” in which the wave motion takes place is called a “medium.”) Waves can be “traveling” or “standing,” and we will start with the traveling kind, since they are the ones that most clearly exhibit the characteristics typically associated with wave motion.
A traveling wave in a medium is a disturbance of the medium that propagates through it, in a definite direction and with a definite velocity. By a “disturbance” we typically mean a displacement of the parts that make up the medium, away from their rest or equilibrium position. The idea here is to regard each part of an elastic medium as, potentially, an oscillator, which couples to the neighboring parts by pushing or pulling on them (for an example of how to model this mathematically, see Advanced Topic 12.6 at the end of this chapter). When the traveling wave reaches a particular location in the medium, it sets that part of the medium in motion, by giving it some energy and momentum, which it then passes on to a neighboring part, and so on down the line.
You can see an example of how this works in a slinky. Start by stretching the slinky somewhat, then grab a few coils, bunch them up at one end, and release them. You should see a “compression pulse” traveling down the slinky, with very little distortion; you may even be able to see it being reflected at the other end, and coming back, before all its energy is dissipated away.
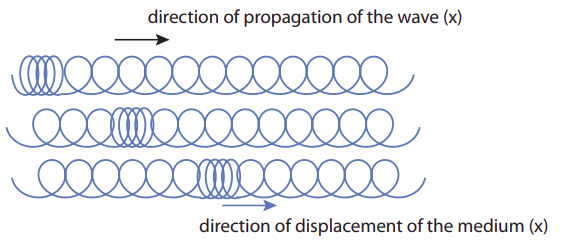
The compression pulse in the slinky in Figure \(\PageIndex{1}\) is an example of what is called a longitudinal wave, because the displacement of the parts that make up the medium (the rings, in this case) takes place along the same spatial dimension along which the wave travels (the horizontal direction, in the figure). The most important examples of longitudinal waves are sound waves, which work a bit like the longitudinal waves on the slinky: a region of air (or some other medium) is compressed, and as it expands it pushes on a neighboring region, causing it to compress, and passing the disturbance along. In the process, regions of rarefaction (where the density drops below its average value) are typically produced, alongside the regions of compression (increased density).
The opposite of a longitudinal wave is a transverse wave, in which the displacement of the medium’s parts takes place in a direction perpendicular to the wave’s direction of travel. It is actually also relatively easy to produce a transverse wave on a slinky: again, just stretch it somewhat and give one end a vigorous shake up and down. It is, however, a little hard to draw the resulting pulse on a long spring with all the coils, so in Figure \(\PageIndex{2}\) below I have instead drawn a transverse wave pulse on a string, which you can produce in the same way. (Strings have other advantages: they are also easier to describe mathematically, and they are very relevant, particularly to the production of musical sounds.)
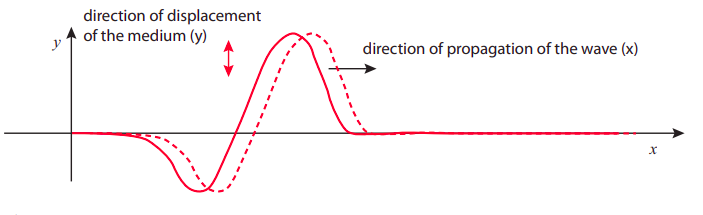
Perhaps the most important (and remarkable) property of wave motion is that it can carry energy and momentum over relatively long distances without an equivalent transport of matter. Again, think of the slinky: the “pulse” can travel through the slinky’s entire length, carrying momentum and energy with it, but each individual ring does not move very far away from its equilibrium position. Ideally, after the pulse has passed through a particular location in the medium, the corresponding part of the medium returns to its equilibrium position and does not move any more: all the energy and momentum it momentarily acquired is passed forward. The same is (ideally) true for the transverse wave on the string in Figure \(\PageIndex{2}\).
Since this is meant to be a very elementary introduction to waves, I will consider only this case of “ideal” (technically known as “linear and dispersion-free”) wave propagation, in which the speed of the wave does not depend on the shape or size of the disturbance. In that case, the disturbance retains its “shape” as it travels, as I have tried to illustrate in figures \(\PageIndex{1}\) and \(\PageIndex{2}\).
The "Wave Shape" Function- Displacement and Velocity of the Medium
In a slinky, what I have been calling the “parts” of the medium are very clearly seen (they are, naturally, the individual rings); in a “homogeneous” medium (one with no visible parts), the way to describe the wave is to break up the medium, in your mind, into infinitely many small parts or “particles” (as we have been doing for extended systems all semester), and write down equations that tell us how each part moves. Physically, you should think of each of these “particles” as being large enough to contain many molecules, but small enough that its position in the medium may be represented by a mathematical point.
The standard way to label each “particle” of the medium is by the position vector of its equilibrium position (the place where the particle sits at rest in the absence of a wave). In the presence of the wave, the particle that was initially at rest at the point \(\vec{r}\) will undergo a displacement that I am going to represent by the vector \(\vec{\xi}\) (where \(\xi\) is the Greek letter “xi”). This displacement will in general be a function of time, and it may also be different for different particles, so it will also be a function of \(\vec{r}\), the equilibrium position of the particle we are considering. The particle’s position under the influence of the wave becomes then
\[ \vec{r}+\vec{\xi}(\vec{r}, t) \label{eq:12.1} .\]
This is very general, and it can be given a simpler form for simple cases. For instance, for a transverse wave on a string, we can label each part of the string at rest by its \(x\) coordinate, and then take the displacement to lie along the \(y\) axis; the position vector, then, could be written in component form as \( (x, \xi(x, t), 0) \). Similarly, we can consider a “plane” sound wave as a longitudinal wave traveling in the \(x\) direction, where the density of the medium is independent of \(y\) and \(z\) (that is, it is constant on planes perpendicular to the direction of propagation). In that case, the equilibrium coordinate \(x\) can be used to refer to a whole “slice” of the medium, and the position of that slice, along the \(x\) axis, at the time \(t\) will be given by \(x+\xi(x, t)\). In both of these cases, the displacement vector \(\xi\) reduces to a single nonzero component (along the \(y\) or \(x\) axis, respectively), which can, of course, be positive or negative. I will restrict myself implicitly to these simple cases and treat \(\xi\) as a scalar from this point on.
Under these conditions, the function \(\xi(x, t)\) (which is often called the wave function) gives us the shape of the “displacement wave,” that is to say, the displacement of every part of the medium, labeled by its equilibrium \(x\)-coordinate, at any instant in time. Accordingly, taking the derivative of \(\xi\) gives us the velocity of the corresponding part of the medium:
\[ v_{\operatorname{med}}=\frac{d \xi}{d t} \label{eq:12.2} .\]
This is also, in general, a vector (along the direction of motion of the wave, if the wave is longitudinal, or perpendicular to it if the wave is transverse). It is also a function of time, and in general will be different from the speed of the wave itself, which we have taken to be constant, and which I will denote by \(c\) instead.
Harmonic Waves
An important class of waves are those for which the wave function is sinusoidal. This means that the different parts of the medium execute simple harmonic motion, all with the same frequency, but each (in general) with a different phase. Specifically, for a sinusoidal wave we have
\[ \xi(x, t)=\xi_{0} \sin \left[\frac{2 \pi x}{\lambda}-2 \pi f t\right] \label{eq:12.3} .\]
In Equation (\ref{eq:12.3}), \(f\) stands for the frequency, and plays the same role it did in the previous chapter: it tells us how often (that is, how many times per second) the corresponding part of the medium oscillates around its equilibrium position. The constant \(\xi_0\) is just the amplitude of the oscillation (what we used to call \(A\) in the previous chapter). The constant \(\lambda\), on the other hand, is sometimes known as the “spatial period,” or, most often, the wavelength of the wave: it tells you how far you have to travel along the \(x\) axis, from a given point \(x\), to find another one that is performing the same oscillation with the same amplitude and phase.
A couple of snapshots of a harmonic wave are shown in Figure \(\PageIndex{3}\). The figure shows the displacement \(\xi\), at two different times, and as a function of the coordinate \(x\) used to label the parts into which we have broken up the medium (as explained in the previous subsection). As such, the wave it represents could equally well be longitudinal or transverse. If it is transverse, like a wave on a string, then you can think of \(\xi\) as being essentially just \(y\), and then the displacement curve (the blue line) just gives you the shape of the string. If the wave is longitudinal, however, then it is a bit harder to visualize what is going on just from the plot of \(\xi (x, t)\). This is what I have tried to do with the density plots at the bottom of the figure.
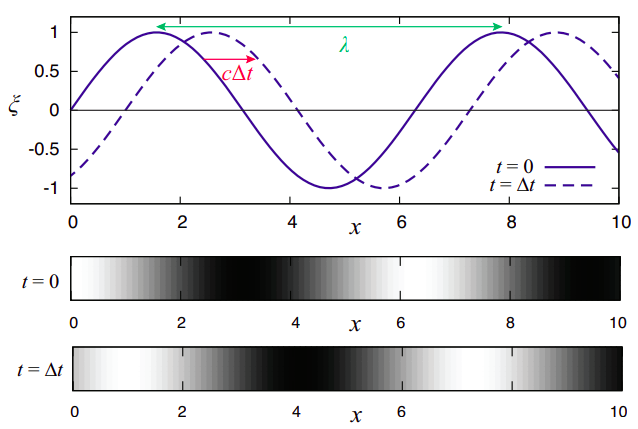
Imagine the wave is longitudinal, and consider the \(x = \pi\) point on the \(t\) = 0 curve (the first zero, not counting the origin). A particle of the medium immediately to the left of that point has a positive displacement, that is, it is pushed towards \(x = \pi\), whereas a slice on the right has a negative displacement—which means it is also pushed towards \(x = \pi\). We therefore expect the density of the medium to be highest around that point, whereas around \(x = 2\pi\) the opposite occurs: particles to the left are pushed to the left and those to the right are pushed to the right, resulting in a low-density region. The density plot labeled \(t\) = 0 attempts to show this using a grayscale where darker and lighter correspond to regions of higher and smaller density, respectively. At the later time \(t = \Delta t\) the high and low density regions have moved a distance \(c\Delta t\) to the right, as shown in the second density plot.
Regardless of whether the wave is longitudinal or transverse, if it is harmonic, the spatial pattern will repeat itself every wavelength; you can think of the wavelength \(\lambda\) as the distance between two consecutive crests (or two consecutive troughs) of the displacement function, as shown in the figure. If the wave is traveling with a speed \(c\), an observer sitting at a fixed point \(x\) would see the disturbance pass through that point, the particles move up and down (or back and forth), and the motion repeat itself after the wave has traveled a distance \(\lambda\), that is, after a time \(\lambda/c\). This means the period of the oscillation at every point is \(T = \lambda/c\), and the corresponding frequency \(f = 1/T = c/ \lambda\):
\[ f=\frac{c}{\lambda} \label{eq:12.4} .\]
This is the most basic equation for harmonic waves. Making use of it, Equation (\ref{eq:12.3}) can be rewritten as
\[ \xi(x, t)=\xi_{0} \sin \left[\frac{2 \pi}{\lambda}(x-c t)\right] \label{eq:12.5} .\]
This suggests that if we want to have a wave moving to the left instead, all we have to do is change the sign of the term proportional to \(c\), which is indeed the case.
In contrast to the wave speed, which is a constant, the speed of any part of the medium, with equilibrium position \(x\), at the time \(t\), can be calculated from Eqs. (\ref{eq:12.2}) and (\ref{eq:12.3}) to be
\[ v_{m e d}(x, t)=2 \pi f \xi_{0} \cos \left[\frac{2 \pi x}{\lambda}-2 \pi f t\right]=\omega \xi_{0} \cos \left[\frac{2 \pi x}{\lambda}-2 \pi f t\right] \label{eq:12.6} \]
(where I have introduced the angular frequency \(\omega = 2\pi f\)). Again, this is a familiar result from the theory of simple harmonic motion: the velocity is “90 degrees out of phase” with the displacement, so it is maximum or minimum where the displacement is zero (that is, when the particle is passing through its equilibrium position in one direction or the other).
Note that the result (\ref{eq:12.6}) implies that, for a longitudinal wave, the “velocity wave” is in phase with the “density wave”: that is, the medium velocity is large and positive where the density is largest, and large and negative where the density is smallest (compare the density plots in Figure \(\PageIndex{3}\)). If we think of the momentum of a volume element in the medium as being proportional to the product of the instantaneous density and velocity, we see that for this wave, which is traveling in the positive \(x\) direction, there is more “positive momentum” than “negative momentum” in the medium at any given time (of course, if the wave had been traveling in the opposite direction, the sign of \(v_{med}\) in Equation (\ref{eq:12.6}) would have been negative, and we would have found the opposite result). This confirms our expectation that the wave carries a net amount of momentum in the direction of propagation. A detailed calculation (which is beyond the scope of this book) shows that the time-average of the “momentum density” (momentum per unit volume) can be written as
\[ \frac{p}{V}=\frac{1}{2 c} \rho_{0} \omega^{2} \xi_{0}^{2} \label{eq:12.7} \]
where \(\rho_{0}\) is the medium’s average mass density (mass per unit volume). Interestingly, this result applies also to a transverse wave!
As mentioned in the introduction, the wave also carries energy. Equation (\ref{eq:12.6}) could be used to calculate the kinetic energy of a small region of the medium (with volume \(V\) and density \(\rho_{0}\), and therefore \(m=\rho_{0} V\)), and its time average. This turns out to be equal to the time average of the elastic potential energy of the same part of the medium (recall that we had the same result for harmonic oscillators in the previous chapter). In the end, the total time-averaged energy density (energy per unit volume) in the region of the medium occupied by the wave is given by
\[ \frac{E}{V}=\frac{1}{2} \rho_{0} \omega^{2} \xi_{0}^{2} \label{eq:12.8} .\]
Comparing (\ref{eq:12.7}) and (\ref{eq:12.8}), you can see that
\[ \frac{E}{V}=\frac{c p}{V} \label{eq:12.9} .\]
This relationship between the energy and momentum densities (one is just \(c\) times the other) is an extremely general result that applies to all sorts of waves, including electromagnetic waves!
The Wave Velocity
You may ask, what determines the speed of a wave in a material medium? The answer, qualitatively speaking, is that \(c\) always ends up being something of the form
\[ c \sim \sqrt{\frac{\text { stiffness }}{\text { inertia }}} \label{eq:12.10} \]
where “stiffness” is some measure of how rigid the material is (how hard it is to compress it or, in the case of a transverse wave, shear it), whereas “inertia” means some sort of mass density.
For a transverse wave on a string, for instance, we find
\[ c=\sqrt{\frac{F t}{\mu}} \label{eq:12.11} \]
where \(F^t\) is the tension in the string and \(\mu\) is not the “reduced mass” of anything (sorry about the confusion!), but a common way to write the “mass per unit length” of the string. We could also just write \(\mu = M/L\), where \(M\) is the total mass of the string and \(L\) its length. Note that the tension is a measure of the stiffness of the string, so this is, indeed, of the general form (\ref{eq:12.10}). For two strings under the same tension, but with different densities, the wave will travel more slowly on the denser one.
For a sound wave in a fluid (liquid or gas), the speed of sound is usually written
\[ c=\sqrt{\frac{B}{\rho_{0}}} \label{eq:12.12} \]
where \(\rho_0\) is the regular density (mass per unit volume), and \(B\) is the so-called bulk modulus, which gives the fluid’s resistance to a change in volume when a pressure \(P\) is applied to it: \(B = P/(\Delta V /V )\). So, once again, we get something of the form (\ref{eq:12.10}). In this case, however, we find that for many fluids the density and the stiffness are linked, so they increase together, which means we cannot simply assume that the speed of sound will be automatically smaller in a denser medium. For gases, this does work well: the speed of sound in a lighter gas, like helium, is greater than in air, whereas in a denser gas like sulfur hexafluoride the speed of sound is less than in air1. However, if you compare the speed of sound in water to the speed of sound in air, you find it is much greater in water, since water is much harder to compress than air: in this case, the increase in stiffness more than makes up for the increase in density.
The same thing happens if you go from a liquid like water to a solid, where the speed of sound is given by
\[ c=\sqrt{\frac{Y}{\rho_{0}}} \label{eq:12.13} \]
where \(Y\) is, again, a measure of the stiffness of the material, called the Young modulus. Since a solid is typically even harder to compress than a liquid, the speed of sound in solids such as metals is much greater than in water, despite their being also denser. For reference, the speed of sound in steel would be about \(c\) = 5,000 m/s; in water, about 1,500 m/s; and in air, “only” about 340 m/s.
1This effect can be used to produce “funny voices,” because of the relationship \(f = c/\lambda\) (Equation (\ref{eq:12.4})), which will be discussed in greater detail in the section on standing waves.
Reflection and Transmission of Waves at a Medium Boundary
Suppose that you have two different elastic media, joined in some way at a common boundary, and you have a wave in the first medium traveling towards the boundary. Examples of media connected this way could be two different strings tied together, or two springs with different spring constants joined at the ends; or, for sound waves, it could just be something like water with air above it: a compression wave in air traveling towards the water surface will push on the surface and set up a sound wave there, and vice-versa.
The first thing to notice is that, if the incident wave has a frequency \(f\), it will cause the medium boundary, when it arrives there, to oscillate at that frequency. As a result of that, the wave that is set up in the second medium—which we call the transmitted wave—will also have the same frequency \(f\). Again, think of the two strings tied together, so the first string “drives” the second one at the frequency \(f\); or the sound at the air-water boundary, driving (pushing) the water surface at the frequency \(f\).
So, the incident and transmitted waves will have the same frequency, but it is clear that, if the wave speeds in the two media are different, they cannot have the same wavelength: since the relation (\ref{eq:12.4}) has to hold, we will have \(\lambda_1 = c_1/f\), and \(\lambda_2 = c_2/f\). Thus, if a periodic wave goes from a slower to a faster medium, its wavelength will increase, and if it goes from a faster to a slower one, the wavelength will decrease.
It is easy to see physically why this happens, and how it has to be the case even for non-periodic waves, that is, wave pulses: a pulse going into a faster medium will widen in length (stretch), whereas a pulse going into a slower medium will become narrower (squeezed). Imagine, for example, several people walking in line, separated by the same distance \(d\), all at the same pace, until they reach a line beyond which they are supposed to start running. When the first person reaches the line, he starts running, but the second one is still walking, so by the time the second one reaches the line the first one has increased his distance from the second. The same thing will happen between the second and the third, and so on: the original “bunch” will become spread out. (If you watch car races, chances are you have seen this kind of thing happen already!)
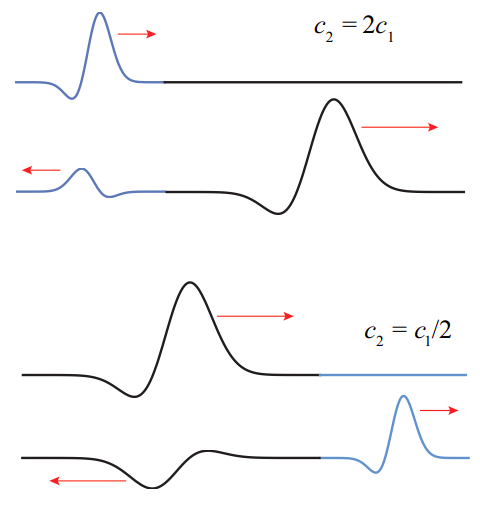
Besides setting up a transmitted wave, with the properties I have just discussed, the incident wave will almost always cause a reflected wave to start traveling in the first medium, moving backwards from the boundary. The reflected wave also has the same frequency as the incident one, and since it is traveling in the same medium, it will also have the same wavelength. A non-periodic pulse, when reflected, will therefore not be stretched or squeezed, but it will be “turned around” back-to-front, since the first part to reach the boundary also has to be the first to leave. See Figure \(\PageIndex{4}\) (the top part) for an example.
What is the physical reason for the reflected wave? Ultimately, it has to do with the energy carried by the incident wave, and whether it is possible for the transmitted wave alone to handle the incoming energy flux or not. As we saw earlier (Equation (\ref{eq:12.8})), the energy per unit volume in a harmonic wave of angular frequency \(\omega\) and amplitude \(\xi_0\) is \(E/V = \frac{1}{2} \rho_{0}\omega^{2}\xi^{2}_{0}\). If the wave is traveling at a speed \(c\), then the energy flux (energy transported per unit time per unit area) is equal to \((E/V )c\), which is to say
\[ I=\frac{1}{2} c \rho_{0} \omega^{2} \xi_{0}^{2} \label{eq:12.14} .\]
This is often called the intensity of the wave. It can be written as \(I=\frac{1}{2} Z \omega^{2} \xi_{0}^{2}\), where I have defined the medium’s mechanical impedance (or simply the impedance) as
\[ Z = c \rho_{0} \label{eq:12.15} \]
(for a string, the mass per unit length \(\mu\) instead of the mass per unit volume \(\rho_0\) should be used). You can see that if the two media have the same impedance, then the energy flux in medium 2 will exactly match that in medium 1, provided the incident and transmitted waves have the same amplitudes. In that case, there will be no reflected wave: even if the two media have different densities and wave velocities, as long as they have the same impedance, the wave will be completely transmitted.
On the other hand, if the media have different impedances, then it will in general be impossible to match the energy flux with only a transmitted wave, and reflection will occur. This is not immediately obvious, since it looks like all you have to do, to compensate for the different impedances in Equation (\ref{eq:12.14}), is to give the transmitted wave an amplitude that is different from that of the incident wave. But the point is precisely that, mathematically, you cannot do that without introducing a reflected wave. This is because the actual amplitude of the oscillation at the boundary has to be the same on both sides, since the two media are connected there, and oscillating together; so, if \(\xi_{0, \text { inc }}\) is going to be different from \(\xi_{0, \text { trans }}\), you need to have another wave in medium 1, the reflected wave, to insure that \(\xi_{0, \text { inc }}+\xi_{0, \text { refl }}=\xi_{0, \text { trans }}\).
Another way to see this is to dig in a little deeper into the physical meaning of the impedance. This is a worthwhile detour, because impedance in various forms recurs in a number of physics and engineering problems. For a sound wave in a solid, for instance, we can see from Eqs. (\ref{eq:12.13}) and (\ref{eq:12.15}) that \(Z = c\rho_0 = \sqrt{Y \rho_0}\); so a medium can have a large impedance either by being very stiff (large \(Y\)) or very dense (large \(\rho_0\)) or both; either way, one would have to work harder to set up a wave in such a medium than in one with a smaller impedance. On the other hand, once the wave is set up, all that work gets stored as energy of the wave, so a wave in a medium with larger \(Z\) will also carry a larger amount of energy (as is also clear from Equation (\ref{eq:12.14}))2 for a given displacement \(\xi_0\).
So, when a wave is trying to go from a low impedance to a large impedance medium, it will find it hard to set up a transmitted wave: the transmitted wave amplitude will be small (compared to that of the incident wave), and the only way to satisfy the condition \(\xi_{0, \text { inc }}+\xi_{0, \text { refl }}=\xi_{0, \text { trans }}\) will be to set up a reflected wave with a negative amplitude3—in effect, to flip the reflected wave upside down, in addition to left-to-right. This is the case illustrated in the bottom drawing in Figure \(\PageIndex{4}\).
Conversely, you might think that a wave trying to go from a high impedance to a low impedance medium would have no trouble setting up a transmitted wave there, and that is true—but because of its low impedance, the transmitted wave will still not be able to carry all the energy flux by itself. In this case, \(\xi_{0,trans}\) will be greater than \(\xi_{0,inc}\), and this will also call for a reflected wave in the first medium, only now it will be “upright,” that is, \(\xi_{0, \text { refl }}=\xi_{0, \text { trans }}-\xi_{0, \text { inc }}>0\).
To finish up the subject of impedance, note that the observation we just made, that impedance will typically go as the square root of the product of the medium’s “stiffness” times its density, is quite general. Hence, a medium’s density will typically be a good proxy for its impedance, at least as long as the “stiffness” factor is independent of the density (as for strings, where it is just equal to the tension) or, even better, increases with it (as is typically the case for sound waves in most materials). Thus, you will often hear that a reflected wave is inverted (flipped upside down) when it is reflected from a denser medium, without any reference to the impedance—it is just understood that “denser” also means “larger impedance” in this case. Also note, along these lines, that a “fixed end,” such as the end of a string that is tied down (or, for sound waves, the closed end of an organ pipe), is essentially equivalent to a medium with “infinite” impedance, in which case there is no transmitted wave at that end, and all the energy is reflected.
Finally, the expression \(\xi_{0,inc} + \xi_{0,refl}\) that I wrote earlier, for the amplitude of the wave in the first medium, implicitly assumes a very important property of waves, which is the phenomenon known as interference, or equivalently, the “linear superposition principle.” According to this principle, when two waves overlap in the same region of space, the total displacement is just equal to the algebraic sum of the displacements produced by each wave separately. Since the displacements are added with their signs, one may get destructive interference if the signs are different, or constructive interference if the signs are the same. This will play an important role in a moment, when we start the study of standing waves.
2In this respect, it may help you to think of the impedance of an extended medium as being somewhat analog to the inertia (mass) of a single particle. The larger the mass, the harder it is to accelerate a particle, but once you have given it a speed v, the larger mass also carries more energy.
3A better way to put this would be to say that the amplitude is positive as always, but the reflected wave is 180\(^{\circ}\) out of phase with the incident wave, so the amplitude of the total wave on the medium 1 side of the boundary is \(\xi_{0,inc} − \xi_{0,refl}\).


