1.7: Units - Displacement and energy

We have now seen two very different kinds of physical systems that exhibit simple harmonic oscillation. Others are possible as well, and we will give another example below. This is a good time to discuss the units of the equations of motions. The “generic” equation of motion for simple harmonic motion without damping looks like this

\[M\frac{d^2X}{dt^2} = −K X\]

where X is the generalized coordinate, M is the generalized mass, K is the generalized spring constant

In the simple harmonic motion of a point mass, X is just the displacement from equilibrium, x, M is the mass, m, and K is the spring constant, K. The appropriate units for M and K depend on the units for X . They are conventionally determined by the requirement that

\[\frac{1}{2}M({\frac{dX}{dt}})^2\]

is the “kinetic” energy of the system arising from the change of the coordinate with time, and

\[\frac{1}{2}KX^2\]

is the “potential” energy of the system, stored in the generalized spring. It makes good physical sense to grant the energy a special status in these problems because in the absence of friction and external forces, the total energy, the sum of the kinetic energy in (1.109) and the potential energy in (1.110), is constant. In the oscillation, the energy is alternately stored in kinetic energy and potential energy. When the system is in its equilibrium configuration, but moving with its maximum velocity, the energy is all kinetic. When the system instantaneously comes to rest at its maximum displacement, all the energy is potential energy. In fact, it is sometimes easier to identify M and K by calculating the kinetic and potential energies than by finding the equation of motion directly. We will use this trick in chapter 11 to discuss water waves. For example, in an LC circuit in SI units, we took our generalized coordinate to be a charge, \(Q\), in Coulombs. Energy is measured in Joules or Volts×Coulombs. The generalized spring constant has units of

\[\dfrac{\text{Joules}}{\text{Coulombs}^2} = \dfrac{\text{Volts}}{\text{Coulombs}}\]

which is one over the unit of capacitance, Coulombs per Volt, or farads. The generalized mass has units of

\[\dfrac{\text{Joules} \times \text{seconds}^2}{\text{Coulombs}^2} = \dfrac{\text{Volts} \times \text{seconds}^2}{\text{Amperes}}\]

which is a unit of inductance (Henrys). This is what we used in our correspondence between the LC circuit and the mechanical oscillator, (1.105). We can also add a generalized force to the right-hand side of (1.107). The generalized force has units of energy over generalized displacement. This is right because when the equation of motion is multiplied by the displacement, (1.109) and (1.110) imply that each of the terms has units of energy. Thus for example, in the LC circuit example, the generalized force is a voltage.

Constant Energy

The total energy is the sum of kinetic plus potential energy from (1.109) and (1.110),

\[E=\frac{1}{2}M(\frac{dX}{dt})^2 +\frac{1}{2}KX^2\]

If there are no external forces acting on the system, the total energy must be constant. You can see from (1.113) that the energy can be constant for an oscillating solution only if the angular frequency, ω, is \(/sqrt{\frac{K}{M}}\). Suppose, for example, that the generalized displacement of the system has the form

\[X(t) = Asin(wt)\]

where A is an amplitude with the units of X . Then the generalized velocity, is

\[\frac{d}{dt}X(t) = Awcos(wt)\]

To make the energy constant, we must have

\[K=w^2M\]

Then, the total energy, from (1.109) and (1.110) is

\[\frac{1}{2}Mw^2A^2cos^2(wt) + \frac{1}{2}KA^2sin^2(wt) = \frac{1}{2}KA^2\]

Torsion Pendulum

One more example may be useful. Let us consider the torsion pendulum, shown in figure 1.14.

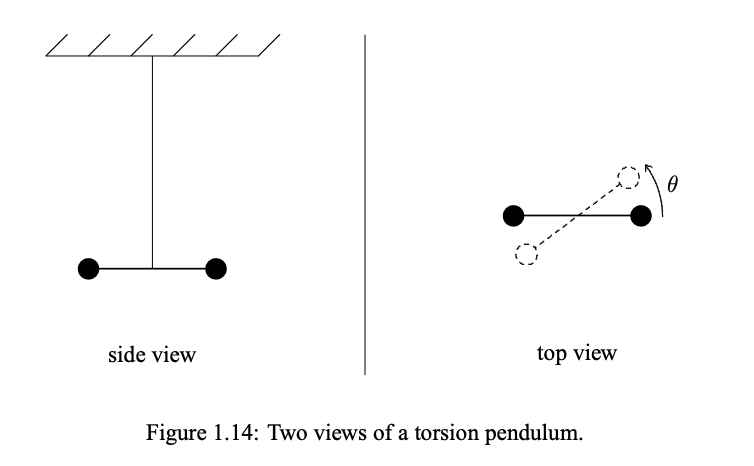
A torsion pendulum is a simple but very useful oscillator consisting of a dumbbell or rod supported at its center by a wire or fiber, hung from a support above. When the dumbbell is twisted by an angle θ, as shown in the top view in figure 1.14, the wire twists and provides a restoring torque on the dumbbell. For a suitable wire or fiber, this restoring torque is nearly linear even for rather large displacement angles. In this system, the natural variable to use for the displacement is the angle θ. Then the equation of motion is

\[I\frac{d^2θ}{dt^2} = −αθ\]

where I is the moment of inertia of the dumbbell about its center and −αθ is the restoring force. Thus the generalized mass is the moment of inertia, I, with units of length squared times mass and the generalized spring constant is the constant α, with units of torque. As expected, from (1.109) and (1.110), the kinetic energy and potential energy are (respectively)

\[\frac{1}{2}(\frac{dθ}{dt})^2 and \frac{1}{2}αθ^2\]