3.6: Chapter Checklist

You should now be able to:

1. Write down the equations of motion for a system with more than one degree of freedom in matrix form;
2. Find the \(M\) and \(K\) matrices from the physics;
3. Add, subtract and multiply matrices;
4. Find the determinant and inverse of \(2 \times 2\) and \(3 \times 3\) matrices;
5. Find normal modes and corresponding frequencies of a system with two degrees of freedom, which means finding the eigenvectors and eigenvalues of a \(2 \times 2\) matrix;
6. Check whether a given vector is a normal mode of a system with more than two degrees of freedom, and if so, find the corresponding angular frequency;
7. Given the normal modes and corresponding frequencies and the initial positions and velocities of all the parts in any system, find the motion of all the parts at all subsequent times;
8. * Go back and forth from normal modes to normal coordinates;
9. * Reconstruct the \(M^{-1}K\) matrix from the normal modes and normal coordinates;
10. * Explicitly solve for the free oscillations of system with two degrees of freedom with damping and be able to analyze systems with three or more degrees of freedom if you are given the eigenvectors;
11. * Explicitly solve forced oscillation problems with or without damping for systems with three or fewer degrees of freedom.

Problems

3.1. The 3 component column vector \(A\), the 3 component row vector \(B\) and the \(3 \times 3\) matrix \(C\) are defined as follows: \[A=\left(\begin{array}{l}
0 \\
2 \\
1
\end{array}\right), \quad B=\left(\begin{array}{lll}
3 & -2 & 1
\end{array}\right), \quad C=\left(\begin{array}{ccc}
1 & 1 & 1 \\
0 & -2 & 1 \\
2 & 2 & 0
\end{array}\right) .\]

Compute the following objects: \[B A, \quad B C, \quad A B.\]

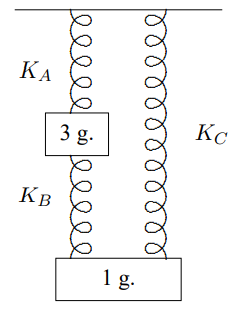
3.2. Consider the vertical oscillation of the system of springs and masses shown below with the spring constants \(K_{A} = 78\), \(K_{B} = 15\) and \(K_{C} = 6\) (all dynes/cm). Find the normal modes, normal coordinates and associated angular frequencies. If the 1 g. block is displaced up 1 cm from its equilibrium position with the 3 g block held at its equilibrium position and both blocks released from rest, describe the subsequent motion of both blocks.

3.3. Consider the system of springs and masses shown below:

with the spring constants in newtons/meter given above the springs and with \(m_{1} = 100\) kg, \(m_{2} = 9\) kg and \(m_{3} = 81\) kg.

1. Which of the following are normal modes of the system and what are the corresponding angular frequencies? Note that the \(M^{-1}K\) matrix may look a little complicated. \[\left(\begin{array}{l}
   \psi_{1} \\
   \psi_{2} \\
   \psi_{3}
   \end{array}\right)=\left(\begin{array}{c}
   9 \\
   0 \\
   10
   \end{array}\right) \quad\left(\begin{array}{c}
   9 \\
   60 \\
   10
   \end{array}\right) \quad\left(\begin{array}{c}
   9 \\
   -30 \\
   10
   \end{array}\right) \quad\left(\begin{array}{c}
   9 \\
   30 \\
   10
   \end{array}\right) \quad\left(\begin{array}{c}
   9 \\
   0 \\
   -10
   \end{array}\right)\]
2. If the system is released from rest with an initial displacement as shown below (with the displacements measured in mm), how long does it take before it first returns to its initial configuration? \[\left(\begin{array}{l}
   \psi_{1} \\
   \psi_{2} \\
   \psi_{3}
   \end{array}\right)=\left(\begin{array}{c}
   9 \\
   0 \\
   10
   \end{array}\right)\]

3.4*. A system of four masses connected by springs is described by a mass matrix, \[M=\left(\begin{array}{llll}
1 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 2
\end{array}\right)\]

and a \(K\) matrix \[K=\left(\begin{array}{cccc}
29 & -10 & -4 & -2 \\
-10 & 58 & -14 & -2 \\
-4 & -14 & 31 & -26 \\
-2 & -2 & -26 & 74
\end{array}\right)\]

1. Which of the following are normal modes? \[\left(\begin{array}{l}
   1 \\
   2 \\
   1 \\
   1
   \end{array}\right)\left(\begin{array}{l}
   1 \\
   1 \\
   2 \\
   1
   \end{array}\right) \quad\left(\begin{array}{l}
   2 \\
   1 \\
   1 \\
   1
   \end{array}\right) \quad\left(\begin{array}{c}
   2 \\
   1 \\
   -1 \\
   -1
   \end{array}\right) \quad\left(\begin{array}{c}
   4 \\
   -3 \\
   0 \\
   1
   \end{array}\right) \quad\left(\begin{array}{c}
   0 \\
   1 \\
   -4 \\
   3
   \end{array}\right)\]
2. For each normal mode, find the corresponding angular frequency. Hint: this requires a little arithmetic. If you are lazy, you might want to use a programmable calculator or write a little computer program to check these for you. But the point of this problem is to show you that the amount of work required to check whether the vectors are normal modes is really tiny compared to the work involved in finding the modes from scratch.
3. If blocks are released from rest from an initial displacement that is proportional to \[\left(\begin{array}{c}
   1 \\
   1 \\
   -1 \\
   1
   \end{array}\right) ,\]
   which normal mode is not present in the subsequent motion?
4. Find the normal coordinates corresponding to each of the normal modes of the system.

3.5. Consider the longitudinal oscillations of the system shown below:

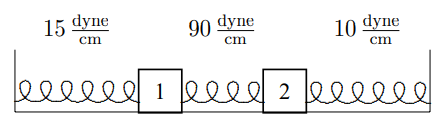
The blocks are free to slide horizontally without friction. The displacements of the blocks from equilibrium are both measured to the right. Block 1 has a mass of 15 grams and block 2 a mass of 10 grams. The spring constants of the springs are shown in dynes/cm.

1. Show that the \(M^{-1}K\) matrix of this system is \[M^{-1} K=\left(\begin{array}{cc}
   7 & -6 \\
   -9 & 10
   \end{array}\right) .\]
2. Show that the normal modes are \[A^{1}=\left(\begin{array}{l}
   1 \\
   1
   \end{array}\right), \quad A^{2}=\left(\begin{array}{c}
   2 \\
   -3
   \end{array}\right) .\]
   Find the corresponding angular frequencies, \(\omega_{1}\) and \(\omega_{2}\).

3.6. Consider the longitudinal oscillations of the system shown below:

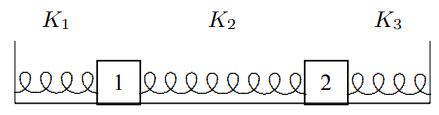
The blocks are free to slide horizontally without friction. The displacements of the blocks from equilibrium are both measured to the right. Block 1 has a mass of 15 grams and block 2 a mass of 10 grams. The spring constants of the springs are \(K_{1}\), \(K_{2}\) and \(K_{3}\), as shown. The normal modes of this system are \[A^{1}=\left(\begin{array}{l}
2 \\
3
\end{array}\right), \quad A^{2}=\left(\begin{array}{c}
1 \\
-1
\end{array}\right)\]

with corresponding frequencies \[\omega_{1}=1 \mathrm{~s}^{-1}, \quad \omega_{2}=2 \mathrm{~s}^{-1} .\]

1. If the system is at rest at time \(t = 0\) with displacements \(x_{1}(0)=5 \mathrm{~cm}\), \(x_{2}(0)=0\), or \[X(0)=\left(\begin{array}{l}
   x_{1}(0) \\
   x_{2}(0)
   \end{array}\right)=\left(\begin{array}{l}
   5 \\
   0
   \end{array}\right) \mathrm{cm} .\]
   Find the displacement of block 2 at time \(t = \pi s\).
2. Find \(K_{1}\), \(K_{2}\) and \(K_{3}\).

3.7*. In the system of problem (3.5), suppose we immerse the system in a damping fluid so that \[\Gamma=\left(\begin{array}{ll}
\gamma & 0 \\
0 & \gamma
\end{array}\right)\]

with \(\gamma = 1 s^{-1}\), and that an external force of the following form is applied (in dynes): \[F(t)=f \cos \omega t=\left(\begin{array}{l}
1 \\
0
\end{array}\right) \cos \omega t .\]

Find and graph the average power lost to the frictional force as a function of \(\omega\) from \(\omega = 0\) to \(10 s^{-1}\).