5.7: Chapter Checklist

Last updated
Save as PDF

Page ID: 45408

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

You should now be able to:

Recognize a finite system as part of a space translation invariant infinite system;
Find the normal modes of the finite system as linear combinations of normal modes of the space translation invariant infinite system, consistent with the physics of the boundaries, by imposing boundary conditions;
Describe the normal modes of a space translation invariant system in terms of an angular wave number, \(k\);
Find the dispersion relation that relates the angular frequency, \(\omega\), to the angular wave number, \(k\);
Solve forced oscillation problems using boundary conditions;
Analyze space translation invariant systems of coupled \(LC\) circuits.

Problems

5.1. Consider the small longitudinal oscillations of the system shown below:

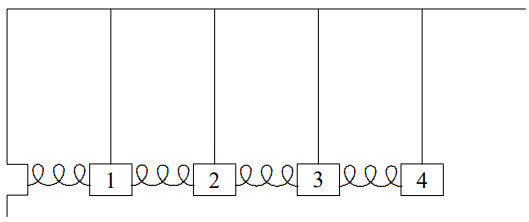
In the picture above, each bob has mass \(m\), each pendulum has length \(\ell\), each spring has spring constant \(\kappa\), and the equilibrium separation between bobs is \(a\).

Find the \(M^{-1}K\) matrix for this system in the basis in which the displacements of the blocks from equilibrium are all measured to the right and arranged into vector in the obvious way, \[X(t)=\left(\begin{array}{l}
x_{1}(t) \\
x_{2}(t) \\
x_{3}(t) \\
x_{4}(t)
\end{array}\right) .\]
Classify as TRUE or FALSE each of the following questions about the normal modes of this system. If possible, explain your answers qualitatively, that is, in words, rather than by plugging into a formula, and discuss the generality of your results.
1. In the normal mode with the lowest frequency, all the blocks move in the same direction when they are moving at all.
2. In the normal mode with the second lowest frequency, the 1st and 2nd blocks have the same displacement.
3. In the normal mode with the highest frequency, neighboring blocks move in opposite directions when they are moving at all.
Find the angular frequencies of each of the normal modes. Hint: You may want to use the dispersion relation for coupled pendulums, \[\omega^{2}=2 B-2 C \cos k a\]

where \[B=\frac{g}{2 \ell}+\frac{\kappa}{m}, \quad C=\frac{\kappa}{m} .\]

5.2.

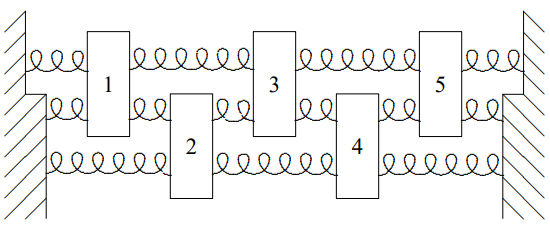
In the system shown above, all the blocks have mass m and they are constrained to move only horizontally. The long springs with six loops have spring constant \(K\). The shorter springs, with three loops, have spring constant \(2K\). The shortest springs, with two loops, have spring constant \(3K\). As you will see in chapter 7, this is what we expect if the springs are all made out of the same material (see Figure \( 7.1\)). Find the normal modes of the system and the corresponding frequencies. Make sure that you justify any assumptions you make about the normal modes. Hint: Try to find an infinite system with space translation invariance that contains this in such a way that you can put in the physics of the walls as a boundary condition. Another Hint: This works simply only if the three loop springs have exactly twice the spring constant of the long springs. Your answer should explain why.

5.3. In the beaded string shown below, the interval between neighboring beads is \(a\), and the distance from the end beads to the walls is \(a / 2\). All the beads have mass \(m\) and are constrained to move only vertically, in the plane of the paper.

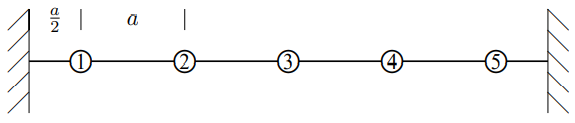
Show that the physics of the left-hand wall can be incorporated by going to an infinite system and requiring the boundary condition \(A_{0} = -A_{1}\).

Easy. Find the analogous boundary condition for the right-hand wall.
Find the normal modes and the corresponding frequencies.

5.4. Consider the following circuit:

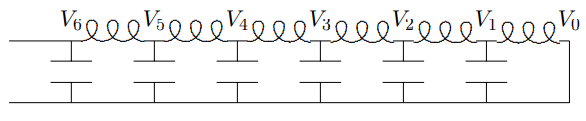
All the capacitors have the same capacitance, \(C \approx 0.00667 \mu F\), and all the inductors have the same inductance, \(L \approx 150 \mu H\) and no resistance. The center wire is grounded. This circuit is an electrical analog of the space translation invariant systems of coupled mechanical oscillators that we have discussed in this chapter.

When you apply a harmonically oscillating signal from a signal generator through a coaxial cable to \(V_{6}\), different oscillating voltages will be induced along the line. That is if \[V_{6}(t)=V \cos \omega t ,\]

then \(V_{j}(t)\) has the form \[V_{j}(t)=A_{j} \cos \omega t+B_{j} \sin \omega t .\]

Find \(A_{j}\) and \(B_{j}\).