7.3: The Speed of Sound

The physics of sound waves is obviously a three-dimensional problem. However, we can learn a lot about sound by considering motion of air in only one-dimension. Consider, for example, standing waves in the air in a long narrow tube like an organ pipe, shown in cartoon form in Figure \( 7.3\). Here, we will ignore the motion of the air perpendicular to the length of the pipe, and consider only the one-dimensional motion along the pipe. As we will see later, when we can deal with three-dimensional problems, this is a sensible thing to do for low frequencies, at which the transverse modes of oscillation cannot be excited. If we consider only one-dimensional motion, we can draw an analogy between the oscillations of the air in the pipe and the longitudinal waves in a massive spring.

Figure 7.3: An organ pipe.

It is clear what the analog of \(\rho_{L}\) is. The linear mass density of the air in the tube is \[\rho_{L}=\rho A\]

where \(A\) is the cross-sectional area of the tube. The question then is what is \(K \ell\) for a tube of air?

Consider putting a piston at the top of the tube, as shown in Figure \( 7.4\). With the piston at the top of the tube, there is no force on the piston, because the pressure of the air in the tube is the same as the pressure of the air in the room outside. However, if the piston is moved in a distance \(dz\), as shown Figure \( 7.5\), the volume of the air in the tube is decreased by \[-d V=A d z .\]

Figure \( 7.4\): The organ pipe with a piston at the top. The air in the tube acts like a spring.

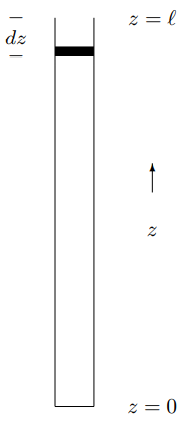
Figure \( 7.5\): Pushing in the piston changes the volume of the air in the tube.

If the piston were moved in slowly enough for the temperature of the gas to stay constant, then the pressure would simply be inversely proportional to the volume. However, in a sound wave, the motion of the air is so rapid that almost no heat has a chance to flow in or out of the system. Such a change in the volume is called “adiabatic.” When the volume is decreased adiabatically, the temperature goes up (because the force on the piston is doing work) and the pressure increases faster than \(1 / V\), like \[p \propto V^{-\gamma}\]

where \(\gamma\) is a positive constant that depends on the thermodynamic properties of the gas. More precisely, \(\gamma\) is the ratio of the specific heat at constant pressure to the specific heat at constant volume:³ \[C_{P} / C_{V}\]

In air, at standard temperature and pressure \[\gamma_{\text {air }} \approx 1.40\]

Now we can write from (7.34), \[\frac{d p}{p}=-\gamma \frac{d V}{V}\]

or \[d p=-\gamma p \frac{d V}{V} \approx \frac{\gamma A p_{0}}{V} d z=\frac{\gamma p_{0}}{\ell} d z\]

where \(p_{0}\) is the equilibrium (room) pressure. Then the force on the piston is \[d F=A d p=\frac{\gamma A^{2} p_{0}}{V} d z=\frac{\gamma A p_{0}}{\ell} d z\]

so that \[K=\frac{d F}{d z}=\frac{\gamma A p_{0}}{\ell}\]

and \(K \ell\) is \[K \ell=\gamma A p_{0} .\]

Thus we expect the dispersion relation to be \[\omega^{2}=v_{\text {sound }}^{2} k^{2}=\frac{K \ell}{\rho_{L}} k^{2}=\frac{\gamma p_{0}}{\rho} k^{2}\]

where we have defined the “speed of sound”, \(v_{\text {sound }}\), as \[v_{\text {sound }}^{2}=\frac{\gamma p_{0}}{\rho}\]

For air at standard temperature and pressure, \[v_{\text {sound }} \approx 332 \frac{\mathrm{m}}{\mathrm{s}} .\]

As we will see in the next chapter, this is actually the speed at which sound waves travel. For now, it is just a parameter in our calculation of the normal modes.

In the pipe shown in (7.3), the displacement of the air, which we will call \(\psi(z,t)\), must vanish at \(z = 0\), because the bottom of the tube is closed and there is nowhere for the gas to go.

The \(z\) derivative of \(\psi\) must vanish at \(z = \ell\), because the excess pressure is proportional to \(-\frac{\partial}{\partial z} \psi\). The pressure is proportional to the force in our analogy with longitudinal waves in ∂z the massive spring. Using (7.41) and (7.23), we expect the longitudinal force to be \[\pm \gamma A p_{0} \frac{\partial}{\partial z} \psi\]

or the excess pressure to be \[p-p_{0}=-\gamma p_{0} \frac{\partial}{\partial z} \psi .\]

We want the negative sign because for \(\frac{\partial}{\partial z} \psi>0\), the air is spreading out and has lower pressure.

Thus for a standing wave in the pipe, (7.3), we expect the boundary conditions \[\psi(0, t)=0,\left.\quad \frac{\partial}{\partial z} \psi(z, t)\right|_{z=\ell}=0 ,\]

for which the solution is \[\psi(z, t)=\sin k z \cos \omega t\]

\[k=\frac{(n+1 / 2) \pi}{\ell}, \quad \omega=v k ,\]

where \(v=v_{\text {sound }}\), for nonnegative integer \(n\). In particular, the lowest frequency mode of the tube corresponds to \(n = 0\), \[\omega=\frac{v \pi}{2 \ell}, \quad \nu=\frac{\omega}{2 \pi}=\frac{v}{4 \ell} .\]

Helmholtz Approximation

Let’s consider a slightly different problem. What is the lowest frequency mode of a one-liter soda bottle, shown in Figure \( 7.6\)? A typical set of parameters is given below: \[\begin{aligned}
&A \approx 2.85 \mathrm{~cm}^{2}: \text { area of neck }\\
&\begin{aligned}
&\ell \approx 5.7 \mathrm{~cm} \quad: \text { length of neck } \\
&L \approx 25 \mathrm{~cm} \quad: \text { length of bottle }
\end{aligned}\\
&V_{0} \approx 1000 \mathrm{~cm}: \text { volume of body }
\end{aligned}\]

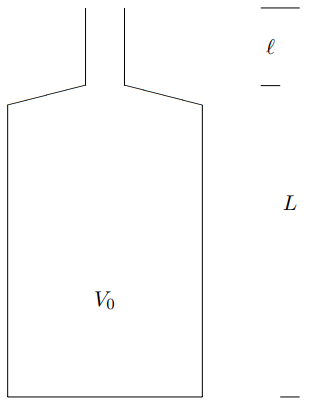
Figure \( 7.6\): A one liter soda bottle.

Putting the length, \(L\), of the bottle into (7.50) gives \(\nu \approx 332 \text { hertz }\). In American standard pitch (see \(Table \text { } 7.1\)), this is an \(E\) above middle \(C\).

This is obviously wrong. If you have ever blown into your soda bottle, you know that the frequency of the lowest mode is much lower than that. The problem, of course, is that the soda bottle is not shaped anything like the tube. To determine the modes is a complicated three-dimensional problem. It turns out, however, that we can find the lowest mode to a decent approximation rather easily.

The idea is that in the lowest mode, the air in the neck of the bottle is moving rapidly, but in the body of the bottle, the air quickly spreads out so that it is not moving much at all. The idea of the Helmholtz approximation to try is to treat the air in the neck as a single chunk with mass \[\rho A \ell ,\]

and to treat the body as a spring, that contributes restoring force but no inertia (because the air is not moving much). Then all we must do is to compute the \(K\) of the “spring.” That is easy, using (7.38). In this case, \[d V=A d z ,\]

so \[d p=-\gamma p \frac{A d z}{V} \approx-\gamma p_{0} \frac{A d z}{V_{0}}\]

\(Table \text { } 7.1\): American standard pitch (A440) — frequencies are in Hertz.

Equal-temperament Chromatic Scale

Note	\(\nu\)	Note	\(\nu\)	Note	\(\nu\)
\(A\)	880	\(A\)	440	\(A\)	220
\(G \#\)	831	\(G #\)	415	\(G #\)	208
\(G\)	784	\(G\)	392	\(G\)	196
\(F \#\)	740	\(F #\)	370	\(F #\)	185
\(F\)	698	\(F\)	349	\(F\)	175
\(E\)	659	\(E\)	330	\(E\)	165
\(E b\)	622	\(E b\)	311	\(E b\)	156
\(D\)	587	\(D\)	294	\(D\)	147
\(C \#\)	554	\(C \#\)	277	\(C \#\)	139
\(C\)	523	\(C\)	262	\(C\)	131
\(B\)	494	\(B\)	247	\(B\)	123
\(B b\)	466	\(B b\)	233	\(B b\)	117

and \[F \approx-\gamma p_{0} \frac{A^{2} d z}{V_{0}}\]

or \[" K "=\gamma p_{0} \frac{A^{2}}{V_{0}} .\]

Then using \(\omega^{2}=K / m\), we expect \[\omega=\sqrt{\frac{\gamma A^{2} p_{0} / V_{0}}{\rho A \ell}}=v \sqrt{\frac{A}{\ell V_{0}}} .\]

For the soda bottle, (7.6), this gives \[\nu \approx 118 \text { hertz }\]

or roughly a \(B b\) below low \(C\). This is just about right (see problem 7.5).

Corrections to Helmholtz

There are many possible corrections to (7.57) that might be considered. One is to include the so-called “end effect.” The point is that the velocity of the air in the lowest mode does not drop to zero immediately when you go past the ends of the neck. Thus the actual mass is somewhat larger than \(\rho A \ell\). The lore is that you can do better by replacing \[\ell \rightarrow \ell+0.6 r\]

where \(r\) is the radius of the neck.

Here we will discuss another correction that can be dealt with systematically using the methods of space translation invariance and local interactions. If the bottle has a long neck, it is probably not a good idea to treat the air in the neck as a solid mass. Furthermore, there is a simple alternative. A better analogy for the neck is a massive spring with \(K \ell=\gamma A p_{0}\). Because the neck is a space translation invariant, essentially one-dimensional system, we expect a displacement of the form \[y \cos \frac{\omega z}{v}\]

in the neck, where \(z = 0\) is the open end and \(y\) is the displacement of the air at \(z = 0\). Thus, where the neck attaches to the body, the displacement is \[y \cos \frac{\omega \ell}{v} .\]

The force at this point from the compression of the air in the neck is (from (7.45)) \[F_{\text {neck }}=-\gamma A p_{0} \frac{\partial \psi}{\partial z}=\frac{\gamma A p_{0} \omega}{v} y \sin \frac{\omega \ell}{v} .\]

This must be the negative of the force from the air in the body, from (7.39), \[-F_{\text {body }}=\frac{\gamma A^{2} p_{0}}{V_{0}} y \cos \omega \ell / v ,\]

or \[\frac{\omega V_{0}}{A v} \tan \frac{\omega \ell}{v}=1 .\]

You will explore the consequences of this in problem 7.5.

This analysis does not distinguish between the area of the top and bottom of the neck. Perhaps the area at the bottom is more appropriate. What matters is the area at the bottom that determines the force per unit area where the wave in the neck matches onto the body.

___________________
³See, for example, Halliday and Resnick.