4.5: Diffraction Gratings
- Last updated
- Oct 10, 2022
- Save as PDF
- Page ID
- 64328
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Discuss the pattern obtained from diffraction gratings
- Explain diffraction grating effects
Analyzing the interference of light passing through two slits lays out the theoretical framework of interference and gives us a historical insight into Thomas Young’s experiments. However, most modern-day applications of slit interference use not just two slits but many, approaching infinity for practical purposes. The key optical element is called a diffraction grating, an important tool in optical analysis.
Diffraction Gratings: An Infinite Number of Slits
The analysis of multi-slit interference in Interference allows us to consider what happens when the number of slits N approaches infinity. Recall that N−2 secondary maxima appear between the principal maxima. We can see there will be an infinite number of secondary maxima that appear, and an infinite number of dark fringes between them. This makes the spacing between the fringes, and therefore the width of the maxima, infinitesimally small. Furthermore, because the intensity of the secondary maxima is proportional to 1/N2, it approaches zero so that the secondary maxima are no longer seen. What remains are only the principal maxima, now very bright and very narrow (Figure 4.5.1).
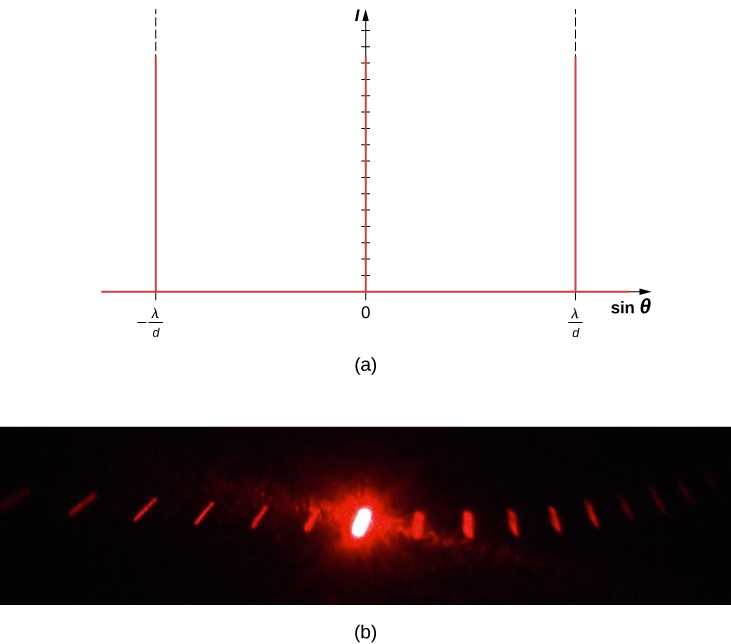
In reality, the number of slits is not infinite, but it can be very large—large enough to produce the equivalent effect. A prime example is an optical element called a diffraction grating. A diffraction grating can be manufactured by carving glass with a sharp tool in a large number of precisely positioned parallel lines, with untouched regions acting like slits (Figure 4.5.2). This type of grating can be photographically mass produced rather cheaply. Because there can be over 1000 lines per millimeter across the grating, when a section as small as a few millimeters is illuminated by an incoming ray, the number of illuminated slits is effectively infinite, providing for very sharp principal maxima.
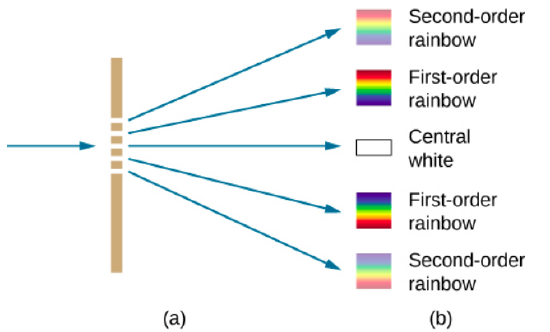
Diffraction gratings work both for transmission of light, as in Figure 4.5.3, and for reflection of light, as on butterfly wings and the Australian opal in Figure 4.5.4a. Natural diffraction gratings also occur in the feathers of certain birds such as the hummingbird. Tiny, finger-like structures in regular patterns act as reflection gratings, producing constructive interference that gives the feathers colors not solely due to their pigmentation. This is called iridescence.

Applications of Diffraction Gratings
Where are diffraction gratings used in applications? Diffraction gratings are commonly used for spectroscopic dispersion and analysis of light. What makes them particularly useful is the fact that they form a sharper pattern than double slits do. That is, their bright fringes are narrower and brighter while their dark regions are darker. Diffraction gratings are key components of monochromators used, for example, in optical imaging of particular wavelengths from biological or medical samples. A diffraction grating can be chosen to specifically analyze a wavelength emitted by molecules in diseased cells in a biopsy sample or to help excite strategic molecules in the sample with a selected wavelength of light. Another vital use is in optical fiber technologies where fibers are designed to provide optimum performance at specific wavelengths. A range of diffraction gratings are available for selecting wavelengths for such use.
Example 4.5.1: Calculating Typical Diffraction Grating Effects
Diffraction gratings with 10,000 lines per centimeter are readily available. Suppose you have one, and you send a beam of white light through it to a screen 2.00 m away.
- Find the angles for the first-order diffraction of the shortest and longest wavelengths of visible light (380 and 760 nm, respectively).
- What is the distance between the ends of the rainbow of visible light produced on the screen for first-order interference? (Figure 4.5.5).
-
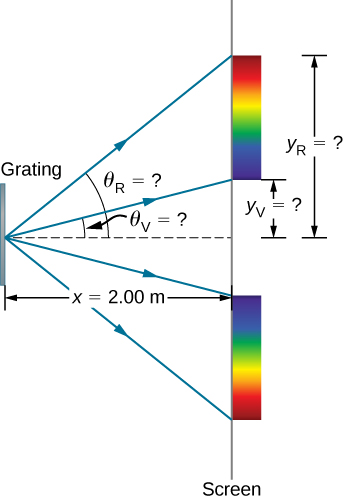
Figure 4.5.5: (a) The diffraction grating considered in this example produces a rainbow of colors on a screen a distance x=2.00m from the grating. The distances along the screen are measured perpendicular to the x-direction. In other words, the rainbow pattern extends out of the page.
(b) In a bird’s-eye view, the rainbow pattern can be seen on a table where the equipment is placed.
Strategy
Once a value for the diffraction grating’s slit spacing d has been determined, the angles for the sharp lines can be found using the equation
dsinθ=mλ
for m=0,±1,±2,....
Since there are 10,000 lines per centimeter, each line is separated by 1/10,000 of a centimeter. Once we know the angles, we an find the distances along the screen by using simple trigonometry.
Solution
- The distance between slits is d=(1cm)/10,000=1.00×10−4cm or 1.00×10−6m. Let us call the two angles θV for violet (380 nm) and θR for red (760 nm). Solving the equation dsinθV=mλ for sinθV,
sinθV=mλVd,
where m = 1 for the first-order and λV=380nm=3.80×10−7m. Substituting these values givessinθV=3.80×10−7m1.00×10−6m=0.380.
Thus the angle θV isθV=sin−10.380=22.33°.
Similarly,sinθR=7.60×10−7m1.00×10−6m=0.760.
Thus the angle θR isθR=sin−10.760=49.46°.
Notice that in both equations, we reported the results of these intermediate calculations to four significant figures to use with the calculation in part (b). - The distances on the screen are labeled yV and yR in Figure 4.5.5. Notice that tanθ=y/x. We can solve for yV and yR. That is,
yV=xtanθV=(2.00m)(tan22.33°)=0.815m
andyR=xtanθR=(2.00m)(tan49.46°)=2.338m.
The distance between them is thereforeyR−yV=1.523m
Significance
The large distance between the red and violet ends of the rainbow produced from the white light indicates the potential this diffraction grating has as a spectroscopic tool. The more it can spread out the wavelengths (greater dispersion), the more detail can be seen in a spectrum. This depends on the quality of the diffraction grating—it must be very precisely made in addition to having closely spaced lines.
Exercise 4.5.1
If the line spacing of a diffraction grating d is not precisely known, we can use a light source with a well-determined wavelength to measure it. Suppose the first-order constructive fringe of the Hβ emission line of hydrogen (λ=656.3nm) is measured at 11.36° using a spectrometer with a diffraction grating. What is the line spacing of this grating?
- Answer
-
3.332×10−6m or 300 lines per millimeter
Take the same simulation we used for double-slit diffraction and try increasing the number of slits from N=2 to N=3,4,5,.... The primary peaks become sharper, and the secondary peaks become less and less pronounced. By the time you reach the maximum number of N=20, the system is behaving much like a diffraction grating.


