13.6: Fission

Learning Objectives

By the end of this section, you will be able to:

• Describe the process of nuclear fission in terms of its product and reactants
• Calculate the energies of particles produced by a fission reaction
• Explain the fission concept in the context of fission bombs and nuclear reactions

In 1934, Enrico Fermi bombarded chemical elements with neutrons in order to create isotopes of other elements. He assumed that bombarding uranium with neutrons would make it unstable and produce a new element. Unfortunately, Fermi could not determine the products of the reaction. Several years later, Otto Hahn and Fritz Strassman reproduced these experiments and discovered that the products of these reactions were smaller nuclei. From this, they concluded that the uranium nucleus had split into two smaller nuclei.

Figure \(\PageIndex{1}\): The Phillipsburg Nuclear Power Plant in Germany uses a fission reactor to generate electricity.

The splitting of a nucleus is called fission. Interestingly, U-235 fission does not always produce the same fragments. Example fission reactions include:

\[\ce{_0^1n + _{92}^{235}U \rightarrow _{56}^{141}Ba + _{36}^{92}Kr + 3_0^1n + Q,} \nonumber \]

\[\ce{_0^1n + _{92}^{235}U \rightarrow _{54}^{140}Xe + _{38}^{94}Sr + 2_0^1n + Q,} \nonumber \]

\[\ce{_0^1n + _{92}^{235}U \rightarrow _{50}^{132}Sn + _{42}^{101}Mo + 3_0^1n + Q,} \nonumber \]

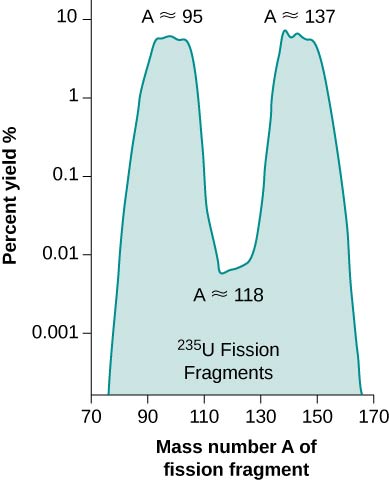
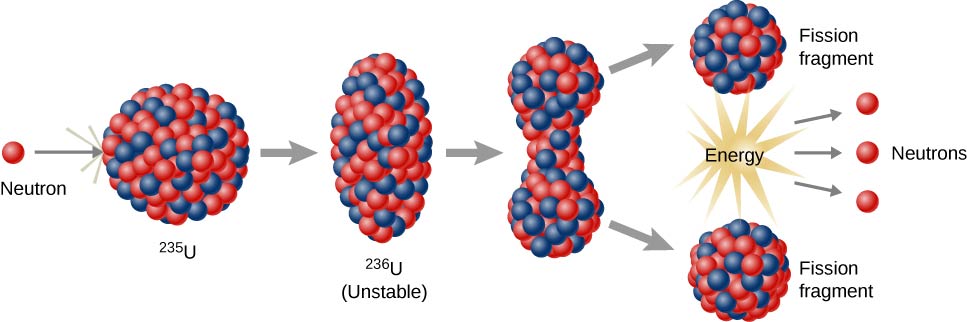
In each case, the sum of the masses of the product nuclei are less than the masses of the reactants, so the fission of uranium is an exothermic process \((Q > 0)\). This is the idea behind the use of fission reactors as sources of energy (Figure \(\PageIndex{1}\)). The energy carried away by the reaction takes the form of particles with kinetic energy. The percent yield of fragments from a U-235 fission is given in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): In this graph of fission fragments from U-235, the peaks in the graph indicate nuclei that are produced in the greatest abundance by the fission process.

Energy changes in a nuclear fission reaction can be understood in terms of the binding energy per nucleon curve. The BEN value for uranium \((A = 236)\) is slightly lower than its daughter nuclei, which lie closer to the iron (Fe) peak. This means that nucleons in the nuclear fragments are more tightly bound than those in the U-235 nucleus. Therefore, a fission reaction results in a drop in the average energy of a nucleon. This energy is carried away by high-energy neutrons.

Niels Bohr and John Wheeler developed the liquid drop model to understand the fission process. According to this model, firing a neutron at a nucleus is analogous to disturbing a droplet of water (Figure \(\PageIndex{3}\)). The analogy works because short-range forces between nucleons in a nucleus are similar to the attractive forces between water molecules in a water droplet. In particular, forces between nucleons at the surface of the nucleus result in a surface tension similar to that of a water droplet. A neutron fired into a uranium nucleus can set the nucleus into vibration. If this vibration is violent enough, the nucleus divides into smaller nuclei and also emits two or three individual neutrons.

Figure \(\PageIndex{3}\): In the liquid drop model of nuclear fission, the uranium nucleus is split into two lighter nuclei by a high-energy neutron.

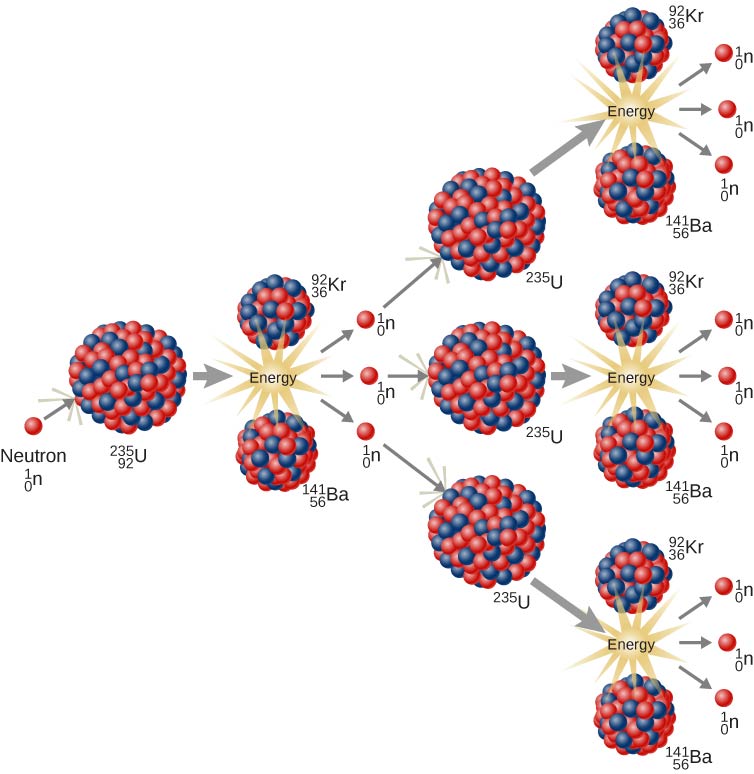
U-235 fission can produce a nuclear chain reaction. In a compound consisting of many U-235 nuclei, neutrons in the decay of one U-235 nucleus can initiate the fission of additional U-235 nuclei (Figure \(\PageIndex{4}\)). This chain reaction can proceed in a controlled manner, as in a nuclear reactor at a power plant, or proceed uncontrollably, as in an explosion.

Figure \(\PageIndex{4}\): In a U-235 fission chain reaction, the fission of the m nucleus produces high-energy neutrons that go on to split more nuclei. The energy released in this process can be used to produce electricity.

View a simulation on nuclear fission to start a chain reaction, or introduce nonradioactive isotopes to prevent one. Control energy production in a nuclear reactor.

The Atomic Bomb

The possibility of a chain reaction in uranium, with its extremely large energy release, led nuclear scientists to conceive of making a bomb—an atomic bomb. (These discoveries were taking place in the years just prior to the Second World War and many of the European physicists involved in these discoveries came from countries that were being overrun.) Natural uranium contains \(99.3\%\) U-238 and only \(0.7\%\) U-235, and does not produce a chain reaction. To produce a controlled, sustainable chain reaction, the percentage of U-235 must be increased to about \(50\%\). In addition, the uranium sample must be massive enough so a typical neutron is more likely to induce fission than it is to escape. The minimum mass needed for the chain reaction to occur is called the critical mass. When the critical mass reaches a point at which the chain reaction becomes self-sustaining, this is a condition known as criticality. The original design required two pieces of U-235 below the critical mass. When one piece in the form of a bullet is fired into the second piece, the critical mass is exceeded and a chain reaction is produced.

An important obstacle to the U-235 bomb is the production of a critical mass of fissionable material. Therefore, scientists developed a plutonium-239 bomb because Pu-239 is more fissionable than U-235 and thus requires a smaller critical mass. The bomb was made in the form of a sphere with pieces of plutonium, each below the critical mass, at the edge of the sphere. A series of chemical explosions fired the plutonium pieces toward the center of the sphere simultaneously. When all these pieces of plutonium came together, the combination exceeded the critical mass and produced a chain reaction. Both the U-235 and Pu-239 bombs were used in World War II. Whether to develop and use atomic weapons remain two of the most important questions faced by human civilization.

Example \(\PageIndex{1}\): Calculating Energy Released by Fission

Calculate the energy released in the following rare spontaneous fission reaction:

\[\ce{^{238}U \rightarrow ^{95}Sr + ^{140}Xe + 3n,} \nonumber \]

The atomic masses are \(m(^{238}U) = 238.050784 \, u\), \(m(^{95}Sr) = 94.919388 \, u\), \(m(^{140}Xe) = 139.921610 \, u\), and \(m(n) = 1.008665 \, u\).

Strategy

As always, the energy released is equal to the mass destroyed times \(c^2\), so we must find the difference in mass between the parent \(^{238}U\) and the fission products.

Solution

The products have a total mass of

\[m_{products} = 94.919388 \, u + 139.921610 \, u + 3(1.008665 \, u) \nonumber \]

\[= 237.866993 \, u. \nonumber \]

The mass lost is the mass of \(^{238}U - m_{products}\) or

\[\Delta m = 238.050784 \, u - 237.8669933 \, u = 0.183791 \, u. \nonumber \]

Therefore, the energy released is

\[E = (\Delta m)c^2 = (0.183791 \, u) \frac{931.5 \, MeV/c^2}{u}c^2 = 171.2 \, MeV. \nonumber \]

Significance

Several important things arise in this example. The energy release is large but less than it would be if the nucleus split into two equal parts, since energy is carried away by neutrons. However, this fission reaction produces neutrons and does not split the nucleus into two equal parts. Fission of a given nuclide, such as \(^{238}U\), does not always produce the same products. Fission is a statistical process in which an entire range of products are produced with various probabilities. Most fission produces neutrons, although the number varies. This is an extremely important aspect of fission, because neutrons can induce more fission, enabling self-sustaining chain reactions.

Fission Nuclear Reactors

The first nuclear reactor was built by Enrico Fermi on a squash court on the campus of the University of Chicago on December 2, 1942. The reactor itself contained U-238 enriched with \(3.6\%\) U-235. Neutrons produced by the chain reaction move too fast to initiate fission reactions. One way to slow them down is to enclose the entire reactor in a water bath under high pressure. The neutrons collide with the water molecules and are slowed enough to be used in the fission process. The slowed neutrons split more U-235 nuclei and a chain reaction occurs. The rate at which the chain reaction proceeds is controlled by a series of “control” rods made of cadmium inserted into the reactor. Cadmium is capable of absorbing a large number of neutrons without becoming unstable.

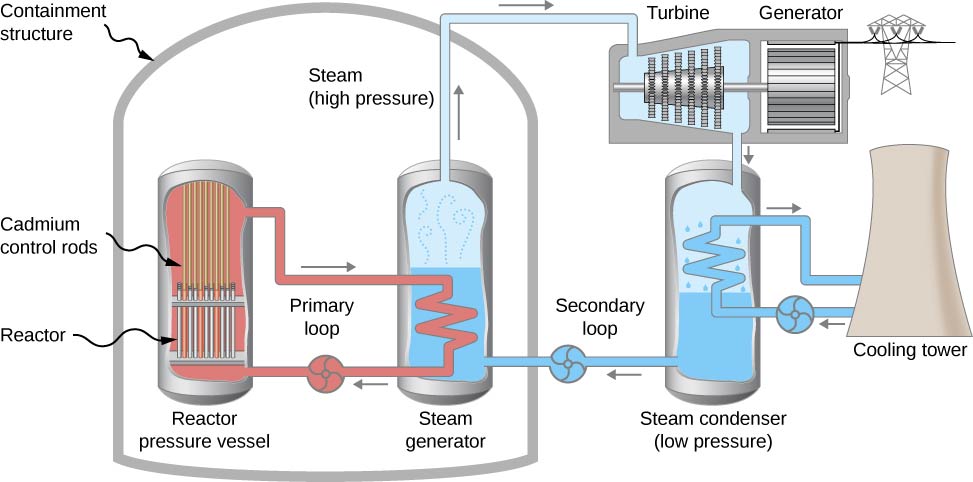
A nuclear reactor design, called a pressurized water reactor, can also be used to generate electricity (Figure \(\PageIndex{5}\)). A pressurized water reactor (on the left in the figure) is designed to control the fission of large amounts of \(^{235}U\). The energy released in this process is absorbed by water flowing through pipes in the system (the “primary loop”) and steam is produced. Cadmium control rods adjust the neutron flux (the rate of flow of neutrons passing through the system) and therefore control the reaction. In case the reactor overheats and the water boils away, the chain reaction terminates, because water is used to thermalize the neutrons. (This safety feature can be overwhelmed in extreme circumstances.) The hot, high-pressure water then passes through a pipe to a second tank of water at normal pressure in the steam generator. The steam produced at one end of the steam generator fills a chamber that contains a turbine. This steam is at a very high pressure. Meanwhile, a steam condenser connected to the other side of the turbine chamber maintains steam at low pressure. The pressure differences force steam through the chamber, which turns the turbine. The turbine, in turn, powers an electric generator.

Figure \(\PageIndex{5}\): A nuclear reactor uses the energy produced in the fission of U-235 to produce electricity. Energy from a nuclear fission reaction produces hot, high-pressure steam that turns a turbine. As the turbine turns, electricity is produced.

The major drawback to a fission reactor is nuclear waste. U-235 fission produces nuclei with long half-lives such as \(^{238}U\) that must be stored. These products cannot be dumped into oceans or left in any place where they will contaminate the environment, such as through the soil, air, or water. Many scientists believe that the best place to store nuclear waste is the bottom of old salt mines or inside of stable mountains.

Many people are fearful that a nuclear reactor may explode like an atomic bomb. However, a nuclear reactor does not contain enough U-235 to do this. Also, a nuclear reactor is designed so that failure of any mechanism of the reactor causes the cadmium control rods to fall fully into the reactor, stopping the fission process. As evidenced by the Fukushima and Chernobyl disasters, such systems can fail. Systems and procedures to avoid such disasters is an important priority for advocates of nuclear energy.

Breeder Reactors

If all electrical power were produced by nuclear fission of U-235, Earth’s known reserves of uranium would be depleted in less than a century. However, Earth’s supply of fissionable material can be expanded considerably using a breeder reactor. A breeder reactor operates for the first time using the fission of U-235 as just described for the pressurized water reactor. But in addition to producing energy, some of the fast neutrons originating from the fission of U-235 are absorbed by U-238, resulting in the production of Pu-239 via the set of reactions

\[\ce{_0^1n + _{92}^{238}U \rightarrow _{92}^{239}U \rightarrow _{93}^{239}Np \rightarrow _{94}^{239}Pu.} \nonumber \]

The Pu-239 is itself highly fissionable and can therefore be used as a nuclear fuel in place of U-235. Since \(99.3\%\) of naturally occurring uranium is the U-238 isotope, the use of breeder reactors should increase our supply of nuclear fuel by roughly a factor of 100. Breeder reactors are now in operation in Great Britain, France, and Russia. Breeder reactors also have drawbacks. First, breeder reactors produce plutonium, which can, if leaked into the environment, produce serious public health problems. Second, plutonium can be used to build bombs, thus increasing significantly the risk of nuclear proliferation.

Example \(\PageIndex{2}\): Calculating Energy of Fissionable Fuel

Calculate the amount of energy produced by the fission of 1.00 kg of \(^{235}U\) given that the average fission reaction of \(^{235}U\) produces 200 MeV.

Strategy

The total energy produced is the number of \(^{235}U\) atoms times the given energy per \(^{235}U\) fission. We should therefore find the number of \(^{235}U\) atoms in 1.00 kg.

Solution

The number of \(^{235}U\) atoms in 1.00 kg is Avogadro’s number times the number of moles. One mole of \(^{235}U\) has a mass of 235.04 g; thus, there are \((1000 \, g)/(235.04 \, g/mol) = 4.25 \, mol\). The number of \(^{235}U\) atoms is therefore

\[(4.25 \, mol)(6.02 \times 10^{23})^{235}U/mol = (2.56 \times 10^{24})^{235}U. \nonumber \]

Thus, the total energy released is

\[E = (2.56 \times 10^{24})^{235}U \left(\frac{200 \, MeV}{^{235}U} \right) \left(\frac{1.60 \times 10^{-13} \, J}{MeV} \right) = 8.21 \times 10^{13} \, J \nonumber \]

Significance

This is another impressively large amount of energy, equivalent to about 14,000 barrels of crude oil or 600,000 gallons of gasoline. However, it is only one-fourth the energy produced by the fusion of a kilogram mixture of deuterium and tritium. Even though each fission reaction yields about 10 times the energy of a fusion reaction, the energy per kilogram of fission fuel is less, because there are far fewer moles per kilogram of the heavy nuclides. Fission fuel is also much scarcer than fusion fuel, and less than \(1\%\) of uranium (the \(^{235}U\)) is readily usable.

Exercise \(\PageIndex{1}\)

Which has a larger energy yield per fission reaction, a large or small sample of pure \(^{235}U\)?

Answer

the same