2.7.9: Solving a System of Linear Equations
- Page ID
- 73611
- Solve a system of equations using the substitution method.
- Recognize systems of equations that have no solution or an infinite number of solutions.
- Solve application problems using the substitution method.
- Solve a system of equations when no multiplication is necessary to eliminate a variable.
- Solve a system of equations when multiplication is necessary to eliminate a variable.
- Recognize systems that have no solution or an infinite number of solutions.
- Solve application problems using the elimination method.
- Solve a system of equations when no multiplication is necessary to eliminate a variable.
- Solve a system of equations when multiplication is necessary to eliminate a variable.
- Solve application problems that require the use of this method.
- Recognize systems that have no solution or an infinite number of solutions.
Using Substitution to Solve a System of Equations
In the substitution method, you solve for one variable and then substitute that expression into the other equation. The important thing here is that you are always substituting values that are equivalent.
For example:
Sean is 5 years older than four times his daughter’s age. His daughter is 7. How old is Sean?
You might do this problem in your head. Sean’s daughter is 7, so “four times his daughter’s age” is 28, and 5 years added to that is 33. Sean is 33.
If you solved the problem like that, you used a simple substitution—you substituted in the value “7” for “his daughter’s age.” You learned in the second part of the problem that “his daughter is 7.” So substituting in a value of “7” for “his daughter’s age” in the first part of the problem was okay, because you knew these two quantities were equal.
Let’s look at a simple system of equations that can be solved using substitution.
Find the value of \(\ x\) for this system.
Equation A: \(\ 4 x+3 y=-14\)
Equation B: \(\ y=2\)
- Solution
-
\(\ \begin{aligned}
4 x+3 y&=-14 \\
y&=2
\end{aligned}\)The problem asks to solve for \(\ x\).
Equation B gives you the value of \(\ y\), \(\ y=2\), so you can substitute 2 into Equation A for \(\ y\).
\(\ 4 x+3(2)=-14\) Substituting \(\ y=2\) into Equation A. \(\ \begin{aligned}
4 x+6&=-14 \\
4 x&=-20 \\
x&=-5
\end{aligned}\)Simplify and solve the equation for \(\ x\). \(\ x=-5\)
You can substitute a value for a variable even if it is an expression. Here’s an example.
Solve for \(\ x\) and \(\ y\).
Equation A: \(\ y+x=3\)
Equation B: \(\ x=y+5\)
- Solution
-
\(\ \begin{array}{l}
y+x=3 \\
x=y+5
\end{array}\)The goal of the substitution method is to rewrite one of the equations in terms of a single variable. Equation \(\ B\) tells us that \(\ x=y+5\), so it makes sense to substitute that \(\ y+5\) into Equation A for \(\ x\). \(\ \begin{array}{r}
y+{\color{blue}x}=3 \\
y+{\color{blue}(y+5)}=3
\end{array}\)Substitute \(\ y+5\) into Equation A for \(\ x\) and you get \(\ y+(y+5)=3\). \(\ \begin{array}{r}
2 y+5&= \ \ \ 3 \\
-5 & -5 \\
\hline 2 y\ \ \ \ \ \ & -2 \\
y\ \ \ \ \ \ &=-1
\end{array}\)Simplify and solve the equation to get \(\ y=-1\). \(\ \begin{array}{r}
y+x&=\ \ 3 \\
-1+x&= \ \ 3 \\
+1\ \ \ \ \ \ \ &+1 \\
\hline x&=\ \ 4
\end{array}\)To now find \(\ x\), substitute this value for \(\ y\) into either equation and solve for \(\ x\). We will use Equation A here to get \(\ x=4\). \(\ \begin{array}{r}
y+x=3 \\
-1+4=3 \\
3=3
\end{array}\)\(\ \begin{array}{r}
x=y+5 \\
4=-1+5 \\
4=4
\end{array}\)TRUE TRUE Finally, check the solution \(\ x=4\), \(\ y=-1\) by substituting these values into each of the original equations. \(\ x=4\) and \(\ y=-1\) The solution is \(\ (4,-1)\).
Remember, a solution to a system of equations must be a solution to each of the equations within the system. The ordered pair \(\ (4,-1)\) works for both equations, so you know that it is a solution to the system as well.
Let’s look at another example whose substitution involves the distributive property.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{c}
y=3 x+6 \\
-2 x+4 y=4
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
y=3 x+6 \\
-2 x+4 y=4
\end{array}\)Choose an equation to use for the substitution.
The first equation tells you how to express \(\ y\) in terms of \(\ x\), so it makes sense to substitute \(\ 3 x+6\) into the second equation for \(\ y\).
\(\ \begin{array}{r}
-2 x+4 {\color{blue}y}=4 \\
-2 x+4{\color{blue}(3 x+6)}=4
\end{array}\)Substitute \(\ 3 x+6\) for \(\ y\) into the second equation. \(\ \begin{array}{r}
-2 x+12 x+24= & 4 \\
10 x+24= & 4 \\
\ -24\ \ \ \ & -24 \\
\hline 10 x\ \ \ \ \ \ \ \ \ = & -20 \\
x\ \ \ \ \ \ \ \ \ = & -2
\end{array}\)Simplify and solve the equation for \(\ x\). \(\ \begin{array}{r}
y=3 x+6 \\
y=3(-2)+6 \\
y=-6+6 \\
y=0
\end{array}\)To find \(\ y\), substitute this value for \(\ x\) back into one of the original equations. \(\ \begin{array}{r}
y=3 x+6 \\
0=3(-2)+6 \\
0=-6+6 \\
0=0
\end{array}\)\(\ \begin{array}{r}
-2 x+4 y=4 \\
-2(-2)+4(0)=4 \\
4+0=4 \\
4=4
\end{array}\)TRUE TRUE Check the solution \(\ x=-2\), \(\ y=0\) by substituting them into each of the original equations. \(\ x=-2\) and \(\ y=0\).
The solution is \(\ (-2,0)\).
In the examples above, one of the equations was already given to us in terms of the variable \(\ x\) or \(\ y\). This allowed us to quickly substitute that value into the other equation and solve for one of the unknowns.
Sometimes you may have to rewrite one of the equations in terms of one of the variables first before you can substitute. Look at the example below.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{c}
2 x+3 y=22 \\
3 x+y=19
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
2 x+3 y=22 \\
3 x+y=19
\end{array}\)Choose an equation to use for the substitution. The second equation, \(\ 3 x+y=19\), can easily be rewritten in terms of \(\ y\), so it makes sense to start there. \(\ \begin{array}{l}
3 x+y=19 \\
y=19-3 x
\end{array}\)Rewrite \(\ 3 x+y=19\) in terms of \(\ y\). \(\ \begin{array}{r}
2 x+3 {\color{blue}y}=22 \\
2 x+3{\color{blue}(19-3 x)}=22
\end{array}\)Substitute \(\ 19-3 x\) for \(\ y\) in the other equation as \(\ 2 x+3(19-3 x)=22\). \(\ \begin{array}{r}
2 x+57-9 x=22 \\
-7 x+57=22 \\
-7 x=-35 \\
x=5
\end{array}\)Simplify and solve the equation for \(\ x\). \(\ \begin{array}{r}
3 x+y=19 \\
3(5)+y=19 \\
15+y=19 \\
y=19-15 \\
y=4
\end{array}\)Substitute \(\ x=5\) back into one of the original equations to solve for \(\ y\). \(\ \begin{aligned}
2 x+3 y &=22 \\
2(5)+3(4) &=22 \\
10+12 &=22 \\
22 &=22
\end{aligned}\)\(\ \begin{aligned}
3 x+y &=19 \\
3(5)+4 &=19 \\
19 &=19
\end{aligned}\)TRUE TRUE Check both solutions by substituting them into each of the original equations. \(\ x=5\) and \(\ y=4\)
The solution is \(\ (5,4)\).
Special Situations
There are some cases where using the substitution method will yield results that, at first, do not make sense. Let’s take a look at some of these and figure out what is going on.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{c}
y=5 x+4 \\
10 x-2 y=4
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
y=5 x+4 \\
10 x-2 {\color{blue}y=4}
\end{array}\)\(\ 10 x-2\color{blue}(5 x+4)=4\)
Since the first equation is \(\ y=5 x+4\), you can substitute \(\ 5 x+4\) in for \(\ y\) in the second equation. \(\ 10 x-10 x-8=4\) Expand the expression on the left. \(\ \begin{aligned}
0-8 &=4 \\
-8 &=4
\end{aligned}\)Combine like terms on the left side of equation.
\(\ 10 x-10 x=0\), so you are left with \(\ -8=4\).
The statement \(\ -8=4\) is false, so there is no solution.
You get the false statement \(\ -8=4\). What does this mean? The graph of this system sheds some light on what is happening.
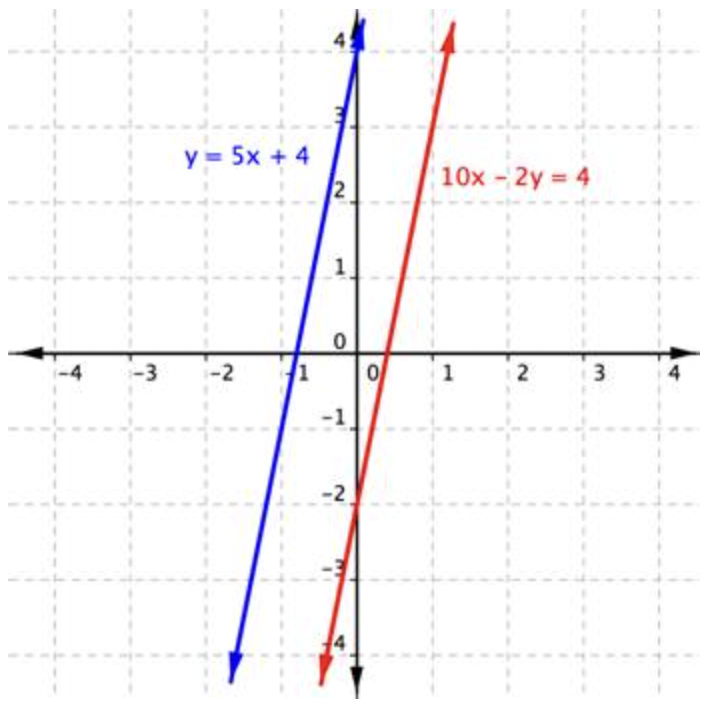
The lines are parallel. They never intersect and there is no solution to this system of linear equations. Note that the result \(\ -8=4\) is not a solution. It is simply a false statement and it indicates that there is no solution.
Now take this problem, which is interesting as well.
\(\ \begin{array}{c}
\color{green}\text { Solve for } x \text { and } y.\\
\color{green}y=-0.5x\\
\color{green}9y=-4.5x
\end{array}\)
Substituting \(\ -0.5 x\) for \(\ y\) in the second equation, you find the following:
\(\ \begin{aligned}
9 y &=-4.5 x \\
9(-0.5 x) &=-4.5 x \\
-4.5 x &=-4.5 x
\end{aligned}\)
This time, you get a true statement: \(\ -4.5 x=-4.5 x\). But what does this type of answer mean? Again, graphing can help you make sense of this system.
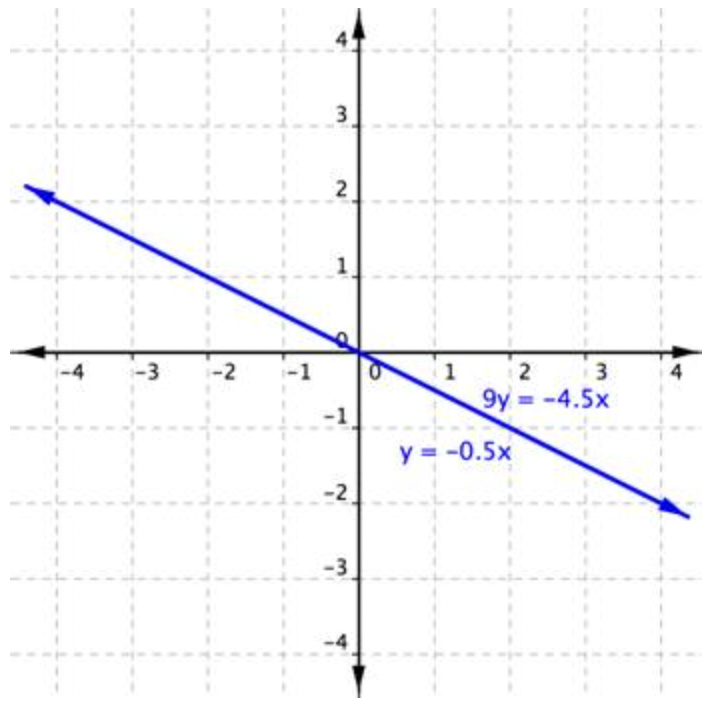
This system consists of two equations that both represent the same line; the two lines are collinear. Every point along the line will be a solution to the system, and that’s why the substitution method yields a true statement. In this case, there are an infinite number of solutions.
Solving Application Problems Using Substitution
Systems of equations are a very useful tool for modeling real-life situations and answering questions about them. If you can translate the application into two linear equations with two variables, then you have a system of equations that you can solve to find the solution. You can use any method to solve the system of equations. Use the substitution method in this topic.
In order to sell more of its produce, a local farm sells bags of apples in two sizes: medium and large. A medium bag contains 4 Macintosh and 1 Granny Smith apples and costs $2.80. A large bag contains 8 Macintosh and 4 Granny Smith apples and costs $7.20. The price of one Granny Smith apple is the same in the medium bag as it is in the large bag. The price of one Macintosh apple is the same in the medium bag as it is in the large bag. What is the price of each kind of apple?
Let’s start by creating a system of equations that represents what is happening in the problem. There are two types of apples and two sizes of bags. You can let \(\ m\) represent the cost of a Macintosh apple and \(\ g\) represent the cost of a Granny Smith apple. Let’s make a table and see what is known.
| Cost of Macintosh apples | + | Cost of Granny Smith apples | = | Total cost of bag | |
| Medium | \(\ 4m\) | + | \(\ g\) | = | $2.80 |
| Large | \(\ 8m\) | + | \(\ 4g\) | = | $7.20 |
Now that you have two equations in the same variables, you can solve the system. You will use substitution. The steps are shown in the example below:
Solve for \(\ g\) and \(\ m\) using the substitution method.
\(\ \begin{array}{c}
4 m+g=2.80 \\
8 m+4 g=7.20
\end{array}\)
- Solution
-
\(\ \begin{array}{l}
4 m+g=2.80 \\
g=2.80-4 m
\end{array}\)First, rewrite one of the equations in terms of one of the variables. \(\ \begin{array}{r}
8 m+4 \color{blue}g=7.20 \\
8 m+4\color{blue}(2.80-4 m)=7.20 \\
8 m+11.20-16 m=7.20 \\
8 m-16 m=7.20-11.20 \\
-8 m=-4.00 \\
m=0.50
\end{array}\)Substitute \(\ (2.80-4 m)\) for \(\ g\) in the second equation and solve for \(\ m\). \(\ \begin{array}{r}
4 m+g=2.80 \\
4(0.5)+g=2.80 \\
2+g=2.80 \\
g=2.80-2 \\
g=0.80
\end{array}\)Substitute the value of \(\ m\), \(\ 0.50\), into one of the original equations to solve for \(\ g\). \(\ \begin{aligned}
4 m+g &=2.80 \\
4(.50)+.80 &=2.80 \\
2.80 &=2.80
\end{aligned}\)Check both equations by substituting in the values of \(\ g\) and \(\ m\). \(\ \begin{aligned}
8 m+4 g &=7.20 \\
8(.50)+4(.80) &=7.20 \\
4.00+3.20 &=7.20 \\
7.20 &=7.20
\end{aligned}\)One Granny Smith apple costs $0.80 and one Macintosh apple costs $0.50.
Using the substitution method can be an effective approach to solving geometric problems.
The perimeter of a rectangle is 60 inches. If the length is 10 inches longer than the width, find the dimensions using the substitution method.
- Solution
-
\(\ \begin{array}{r}
2 l+2 w=60 \\
l=w+10
\end{array}\)Use the information provided to write a system of equations. Let \(\ l=\text { length }\) and \(\ w=\text { width }\). \(\ \begin{array}{r}
2 {\color{blue}l}\ \ \ \ \ \ \ \ \ \ \ \ \ +2 w&= \ \ \ 60 \\
2{\color{blue}(w+10)}+2 w & =\ \ \ 60 \\
2 w\ \ \ +20\ \ \ \ \ +2 w & =\ \ \ 60 \\
4 w\ \ \ \ \ +20&= \ \ \ 60 \\
-20 & -20 \\
\hline 4 w&=\ \ \ 40 \\
w&= \ \ \ 10
\end{array}\)Substitute \(\ w+10\) for \(\ l\) in the first equation and solve for \(\ w\). \(\ \begin{array}{r}
l=w+10 \\
l=10+10 \\
l=20
\end{array}\)To find \(\ l\), substitute 10 for \(\ w\) in one of the equations and solve for \(\ l\). \(\ \begin{array}{r}
l=w+10 \\
20=10+10 \\
20=20
\end{array}\)Check both solutions by substituting them into the two equations. \(\ \begin{array}{r}
2 l+2 w=60 \\
2(20)+2(10)=60 \\
40+20=60 \\
60=60
\end{array}\)Both of them are true, so this is a correct solution. The length of the rectangle is 20 inches.
The width of the rectangle is 10 inches.
Solving a System of Equations Using the Elimination Method
The elimination method for solving systems of linear equations uses the addition property of equality. You can add the same value to each side of an equation.
So if you have a system: \(\ x-y=-6\) and \(\ x+y=8\), you can add \(\ x+y\) to the left side of the first equation and add 8 to the right side of the equation. And since \(\ x+y=8\), you are adding the same value to each side of the first equation.
Using Addition to Eliminate a Variable
If you add the two equations, \(\ x-y=-6\) and \(\ x+y=8\) together, as noted above, watch what happens.
\(\ \begin{array}{rr}
x-y= & -6 \\
x+y= & 8 \\
\hline 2 x+0= & 2
\end{array}\)
You have eliminated the \(\ y\) term, and this equation can be solved using the methods for solving equations with one variable.
Let’s see how this system is solved using the elimination method.
Use elimination to solve the system.
\(\ \begin{array}{c}
x-y=-6 \\
x+y=8
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
x-y= & -6 \\
+\quad x+y= & 8 \\
\hline 2 x \ \ \ \ \ \ \ =&2
\end{array}\)Add the equations. \(\ \begin{aligned}
2 x &=2 \\
x &=1
\end{aligned}\)Solve for \(\ x\). \(\ \begin{array}{r}
x+y=8 \\
1+y=8 \\
y=8-1 \\
y=7
\end{array}\)Substitute \(\ x=1\) into one of the original equations and solve for \(\ y\). \(\ \begin{array}{r}
x-y=-6 \\
1-7=-6 \\
-6=-6
\end{array}\)\(\ \begin{aligned}
x+y &=8 \\
1+7 &=8 \\
8 &=8
\end{aligned}\)TRUE TRUE Be sure to check your answer in both equations!
The answers check.
The solution is \(\ (1,7)\).
Unfortunately, not all systems work out this easily. How about a system like \(\ 2 x+y=12\) and \(\ -3 x+y=2\)? If you add these two equations together, no variables are eliminated.
\(\ \begin{aligned}
2 x+y&=12 \\
-3 x+y&=2 \\
\hline-x+2 y&=14
\end{aligned}\)
But you want to eliminate a variable. So let’s add the opposite of one of the equations to the other equation.
\(\ \begin{array}{r}
2 x+y=12 \quad \rightarrow& 2 x+y=12\quad \rightarrow& \quad 2 x+y=\ 12 \\
-3 x+y=2 \quad\rightarrow&-(-3 x+y)=-(2)\quad \rightarrow& \quad \underline{3x-y=-2}\\
&& 5x+0y=\ 10
\end{array}\)
You have eliminated the \(\ y\) variable, and the problem can now be solved. See the example below.
Use elimination to solve the system.
\(\ \begin{aligned}
2 x+y&=12 \\
-3 x+y&=2
\end{aligned}\)
- Solution
-
\(\ \begin{aligned}
2 x+y&=12 \\
-3 x+y&=2
\end{aligned}\)You can eliminate the y-variable if you add the opposite of one of the equations to the other equation. \(\ \begin{aligned}
2 x+y&=12 \\
3 x-y&=-2 \\
5 x&=10
\end{aligned}\)Rewrite the second equation as its opposite.
Add.
\(\ x=2\) Solve for \(\ x\). \(\ \begin{array}{r}
2(2)+y=12 \\
4+y=12 \\
y=8
\end{array}\)Substitute \(\ x=2\) into one of the original equations and solve for \(\ y\). \(\ \begin{array}{r}
2 x+y=12 \\
2(2)+8=12 \\
4+8=12 \\
12=12
\end{array}\)\(\ \begin{array}{r}
-3 x+y=2 \\
-3(2)+8=2 \\
-6+8=2 \\
2=2
\end{array}\)TRUE TRUE Be sure to check your answer in both equations!
The answers check.
The solution is \(\ (2,8)\).
The following are two more examples showing how to solve linear systems of equations using elimination.
Use elimination to solve the system.
\(\ \begin{aligned}
-2 x+3 y&=-1 \\
2 x+5 y&=25
\end{aligned}\)
- Solution
-
\(\ \begin{aligned}
-2 x+3 y &=-1 \\
2 x+5 y &=25
\end{aligned}\)Notice the coefficients of each variable in each equation. If you add these two equations, the \(\ x\) term will be eliminated since \(\ -2 x+2 x=0\). \(\ \begin{array}{rr}
-2 x+3 y= & -1 \\
2 x+5 y= & 25 \\
\hline 8 y= & 24 \\
y= & 3
\end{array}\)Add and solve for \(\ y\). \(\ \begin{aligned}
2 x+5 y&=25 \\
2 x+5(3)&=25 \\
2 x+15&=25 \\
2 x&=10 \\
x&=5
\end{aligned}\)Substitute \(\ y=3\) into one of the original equations. \(\ \begin{aligned}
-2 x+3 y &=-1 \\
-2(5)+3(3) &=-1 \\
-10+9 &=-1 \\
-1 &=-1
\end{aligned}\)\(\ \begin{array}{r}
2 x+5 y=25 \\
2(5)+5(3)=25 \\
10+15=25 \\
25=25
\end{array}\)TRUE TRUE Check solutions.
The answers check.
The solution is \(\ (5,3)(5,3)\).
Use elimination to solve for \(\ x\) and \(\ y\).
- Solution
-
\(\ \begin{array}{l}
4 x+2 y=14 \\
5 x+2 y=16
\end{array}\)Notice the coefficients of each variable in each equation. You will need to add the opposite of one of the equations to eliminate the variable \(\ y\), as \(\ 2 y+2 y=4 y\), but \(\ 2 y+(-2 y)=0\). \(\ \begin{array}{r}
4 x+2 y= & 14 \\
-5 x-2 y= & -16 \\
\hline-x \ \ \ \ \ \ \ \ \ = & -2 \\
x\ \ \ \ \ \ \ \ \ = & 2
\end{array}\)Change one of the equations to its opposite, add and solve for \(\ x\). \(\ \begin{aligned}
4 x+2 y=&14 \\
4(2)+2 y=&14 \\
8+2 y=&14 \\
2 y=&6 \\
y=&3
\end{aligned}\)Substitute \(\ x=2\) into one of the original equations and solve for \(\ y\). The solution is \(\ (2,3)\).
Go ahead and check this last example—substitute \(\ (2,3)\) into both equations. You get two true statements: \(\ 14=14\) and \(\ 16=16\)!
Notice that you could have used the opposite of the first equation rather than the second equation and gotten the same result.
Using Multiplication and Addition to Eliminate a Variables
Many times, adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Look at the system below.
\(\ \begin{aligned}
3 x+4 y=52 \\
5 x+y=30
\end{aligned}\)
If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. So let’s now use the multiplication property of equality first. You can multiply both sides of one of the equations by a number that will result in the coefficient of one of the variables being the opposite of the same variable in the other equation.
This is where multiplication comes in handy. The first equation contains the term \(\ 4y\) and the second equation contains the term \(\ y\). If you multiply the second equation by -4, when you add both equations, the \(\ y\) variables will add up to 0.
\(\ \begin{array}{l}
3 x+4 y=52 \quad&\rightarrow \quad3 x+4 y=52 \quad&\rightarrow \quad3 x+4 y= 52 \\
5 x+y=30 \quad&\rightarrow \quad-4(5 x+y)=-4(30) \quad&\rightarrow \quad\underline{-20 x-4 y=-120}\\
&&\quad-17x+0y=-68
\end{array}\)
See the example below.
Solve for \(\ x\) and \(\ y\).
Equation A: \(\ 3 x+4 y=52\)
Equation B: \(\ 5 x+y=30\)
- Solution
-
\(\ \begin{array}{r}
3 x+4 y=52 \\
5 x+\ \ y=30
\end{array}\)Look for terms that can be eliminated. The equations do not have any \(\ x\) or \(\ y\) terms with the same coefficients. \(\ \begin{aligned}
3 x+4 y&=52 \\
-4 (5 x+y)&=-4(30) \\
\hline
\end{aligned}\)Multiply the second equation by -4 so they have the same coefficient. \(\ \begin{array}{rr}
3 x+4 y= & 52 \\
-20 x-4 y= & -120 \\
\hline
\end{array}\)Rewrite the system, and add the equations. \(\ \begin{aligned}
-17 x &=-68 \\
x &=4
\end{aligned}\)Solve for \(\ x\). \(\ \begin{array}{r}
3 x+4 y=52 \\
3(4)+4 y=52 \\
12+4 y=52 \\
4 y=40 \\
y=10
\end{array}\)Substitute \(\ x=4\) into one of the original equations to find \(\ y\). \(\ \begin{array}{r}
3 x+4 y=52 \\
3(4)+4(10)=52 \\
12+40=52 \\
52=52
\end{array}\)\(\ \begin{array}{r}
5 x+y=30 \\
5(4)+10=30 \\
20+10=30 \\
30=30
\end{array}\)TRUE TRUE Check your answer.
The answers check.
The solution is \(\ (4,10)\).
There are other ways to solve this system. Instead of multiplying one equation in order to eliminate a variable when the equations were added, you could have multiplied both equations by different numbers.
Let’s remove the variable \(\ x\) this time. Multiply Equation A by 5 and Equation B by -3.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{r}
3 x+4 y=52 \\
5 x+\ \ y=30
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
3 x+4 y=52 \\
5 x+\ \ y=30
\end{array}\)Look for terms that can be eliminated. The equations do not have any \(\ x\) and \(\ y\) terms with the same coefficient. \(\ \begin{aligned}
5(3 x+4 y) &=5(52) \\
5 x+\ y\ \ &=0
\end{aligned}\)\(\ \begin{aligned}
15 x+20 y&=260\\
5 x+y&=30
\end{aligned}\)In order to use the elimination method, you have to create variables that have the same coefficient—then you can eliminate them. Multiply the top equation by 5. \(\ \begin{aligned}
15 x+20 y&=260 \\
-3(5 x+\ \ y)&=-3(30)
\end{aligned}\)\(\ \begin{array}{r}
15 x+20 y=& 260 \\
-15 x-\ \ 3 y=&-90
\end{array}\)Now multiply the bottom equation by -3. \(\ \begin{array}{r}
15 x+20 y &=&+260 \\
-15 x-\ \ 3 y &=&- 90 \\
\hline 17 y &=& 170 \\
y &=& 10
\end{array}\)Next add the equations, and solve for \(\ y\). \(\ \begin{aligned}
3 x+4 y&=52 \\
3 x+4(10)&=52 \\
3 x+40&=52 \\
3 x&=12 \\
x&=4
\end{aligned}\)Substitute \(\ y=10\) into one of the original equations to find \(\ x\). The solution is \(\ (4,10)\). You arrive at the same solution as before.
These equations were multiplied by 5 and -3 respectively, because that gave you terms that would add up to 0. Be sure to multiply all of the terms of the equation.
Special Situations
Just as with the substitution method, the elimination method will sometimes eliminate both variables, and you end up with either a true statement or a false statement. Recall that a false statement means that there is no solution.
Let’s look at an example.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{c}
-x-y=-4 \\
x+y=2
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
-x-y&=&-4 \\
x+y&=&2 \\
\hline 0&=&-2
\end{array}\)Add the equations to eliminate the x-term. There is no solution.
Graphing these lines shows that they are parallel lines and as such do not share any point in common, verifying that there is no solution.
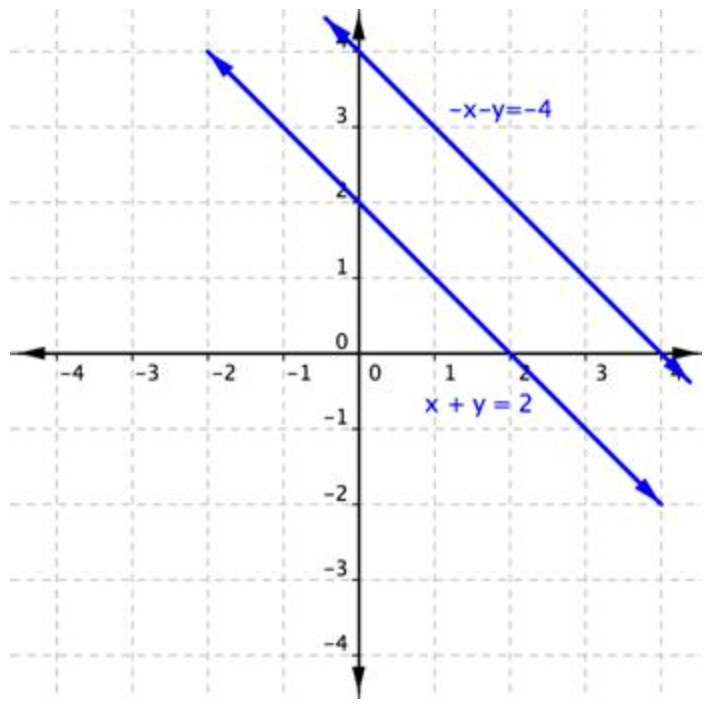
If both variables are eliminated and you are left with a true statement, this indicates that there are an infinite number of ordered pairs that satisfy both of the equations. In fact, the equations are the same line.
Solve for \(\ x\) and \(\ y\).
\(\ \begin{array}{r}
x+y&=&2 \\
-x-y&=&-2
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
x+y&=&2 \\
-x-y&=&-2 \\
\hline 0&=&0
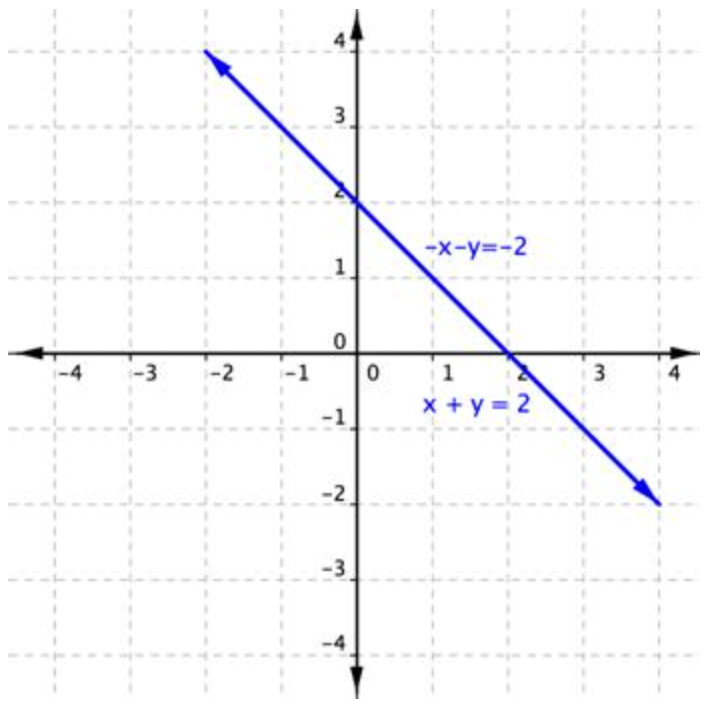
\end{array}\)Add the equations to eliminate the x-term. There are an infinite number of solutions.
Graphing these two equations will help to illustrate what is happening.
Solving Application Problems Using the Elimination Method
The elimination method can be applied to solving systems of equations that model real situations. Two examples of using the elimination method in problem solving are shown below.
The sum of two numbers is 10. Their difference is 6. What are the two numbers?
- Solution
-
\(\ \begin{array}{r}
x+y&=&10 \\
x-y&=&6
\end{array}\)Write a system of equations to model the situation.
\(\ x\)=one number
\(\ y\)=the other number
\(\ \begin{array}{r}
x+y &=&10 \\
+\quad x-y &=&6 \\
\hline 2 x &=&16 \\
x &=&8
\end{array}\)Add the equations to eliminate the y-term and then solve for \(\ x\). \(\ \begin{array}{r}
x+y&=&10 \\
8+y&=&10 \\
y&=&2
\end{array}\)Substitute the value for \(\ x\) into one of the original equations to find \(\ y\). \(\ \begin{array}{r}
x+y=10 \\
8+2=10 \\
10=10
\end{array}\)\(\ \begin{array}{r}
x-y=6 \\
8-2=6 \\
6=6
\end{array}\)TRUE TRUE Check your answer by substituting \(\ x=8\) and \(\ y=2\) into the original system.
The answers check.
The numbers are 8 and 2.
A theater sold 800 tickets for Friday night’s performance. One child ticket costs $4.50 and one adult ticket costs $6.00. The total amount collected was $4,500. How many of each type of ticket were sold?
- Solution
-
The total number of tickets sold is \(\ 800\).
\(\ a+c=800\)
The amount of money collected is \(\ $4,500\)
\(\ 6 a+4.5 c=4,500\)
System of equations:
\(\ a+c=800\)
\(\ 6 a+4.5 c=4,500\)
Write a system of equations to model the ticket sale situation.
\(\ a\)=number of adult tickets sold
\(\ c\)=number of child tickets sold
\(\ \begin{array}{r}
6(a+c)=6(800) \\
6 a+4.5 c=4,500
\end{array}\)\(\ \begin{array}{r}
6 a+6 c=4,800 \\
6 a+4.5 c=4,500
\end{array}\)Use multiplication to re-write the first equation. \(\ \begin{array}{r}
6 a+6 c&=&4,800 \\
-6 a-4.5 c&=&-4,500 \\
\hline 1.5 c&=&300
\end{array}\)\(\ c= 200\)
Add the opposite of the second equation to eliminate a term and solve for \(\ c\). \(\ \begin{array}{r}
a+200&=&800 \\
-200&&-200 \\
\hline a&=&600
\end{array}\)Substitute 200 in for \(\ c\) in one of the original equations. \(\ \begin{aligned}
a+c &=800 \\
600+200 &=800 \\
800 &=800
\end{aligned}\)\(\ \begin{array}{r}
6 a+4.5 c=4,500 \\
6(600)+4.5(200)=4,500 \\
3,600+900=4,500 \\
4500=4,500
\end{array}\)TRUE TRUE Check your answer by substituting \(\ a=600\) and \(\ c=200\) into the original system.
The answers check.
600 adult tickets and 200 child tickets were sold.
Solving A System of Three Linear Equations with Three Variables
Equations can have more than one or two variables. You are going to look at equations with three variables. Equations with one variable graph on a line. Equations with two variables graph on a plane. Equations with three variables graph in a 3-dimensional space.
Equations with one variable require only one equation to have a unique (one) solution. Equations with two variables require two equations to have a unique solution (one ordered pair). So it should not be a surprise that equations with three variables require a system of three equations to have a unique solution (one ordered triplet).
Solving A System of Three Variables
Just as when solving a system of two equations, there are three possible outcomes for the solution of a system of three variables. Let’s look at this visually, although you will not be graphing these equations.
Case 1: There is one solution. In order for three equations with three variables to have one solution, the planes must intersect in a single point.
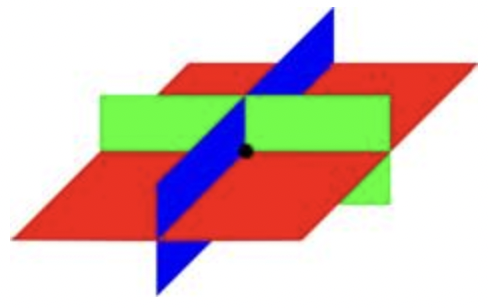
Case 2: There is no solution. The three planes do not have any points in common. (Note that two of the equations may have points in common with each other, but not all three.) Below are examples of some of the ways this can happen.
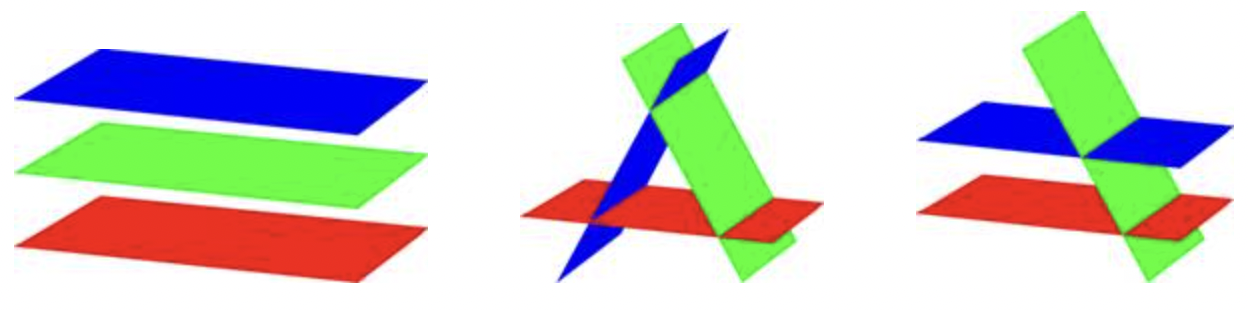
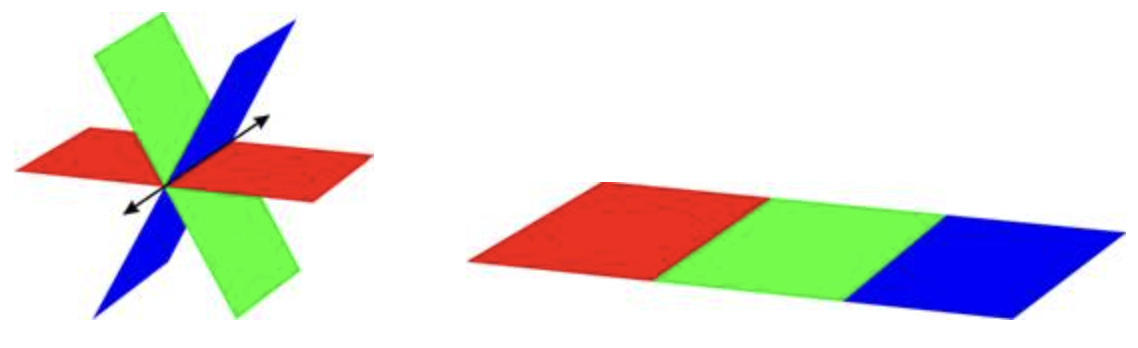
Case 3: There are an infinite number of solutions. This occurs when the three planes intersect in a line. And this can also occur when the three equations graph as the same plane.
Let’s start by looking at Case 1, where the system has a unique (one) solution. This is the case that you are usually most interested in.
Here is a system of linear equations. There are three variables and three equations.
\(\ \begin{array}{l}
3 x+4 y-z=8 \\
5 x-2 y+z=4 \\
2 x-2 y+z=1
\end{array}\)
You know how to solve a system with two equations and two variables. For the first step, use the elimination method to remove one of the variables. In this case, \(\ z\) can be eliminated by adding the first and second equations.
\(\ \begin{aligned}
3 x+4 y-z&=\ \ 8 \\
5 x-2 y+z&=\ \ 4 \\
\hline 8 x+2 y\ \ \ \ \ \ \ &=12
\end{aligned}\)
To solve the system, though, you need two equations using two variables. Adding the first and third equations in the original system will also give an equation with \(\ x\) and \(\ y\) but not \(\ z\).
\(\ \begin{array}{r}
3 x+4 y-z=8 \\
2 x-2 y+z=1 \\
\hline 5 x+2 y\ \ \ \quad=9
\end{array}\)
Now you have a system of two equations and two variables.
\(\ \begin{array}{r}
8 x+2 y=12 \\
5 x+2 y\ \ =9
\end{array}\)
Solve the system using elimination again. In this case, you can eliminate \(\ y\) by adding the opposite of the second equation:
\(\ \begin{array}{r}
8 x+\ \ \ 2 y &=&12 \\
-5 x+-2 y &=&-9 \\
\hline 3 x\ \ \ \ \ \ \ \ \ \ \ \ &=&3
\end{array}\)
Solve the resulting equation for the remaining variable.
\(\ \begin{array}{r}
3 x=3 \\
x=1
\end{array}\)
Now you use one of the equations in the two-variable system to find \(\ y\).
\(\ \begin{array}{r}
5 x+2 y=9 \\
5(1)+2 y=9 \\
5+2 y=9 \\
2 y=4 \\
y=2
\end{array}\)
Finally, use any equation from the first system, along with the values already found, to solve for the last variable.
\(\ \begin{array}{r}
2 x-2 y+z=1 \\
2(1)-2(2)+z=1 \\
2-4+z=1 \\
-2+z=1 \\
z=3
\end{array}\)
Be sure to check your answer. With this many steps, there are a lot of places to make a simple error!
\(\ \begin{array}{r}
3 x+4 y-z=8 \\
3(1)+4(2)-3=8 \\
3+8-3=8 \\
11-3=8 \\
8=8 \\
\text { TRUE }
\end{array}\)
\(\ \begin{array}{r}
5 x-2 y+z=4 \\
5(1)-2(2)+3=4 \\
5-4+3=4 \\
1+3=4 \\
4=4 \\
\text { TRUE }
\end{array}\)
\(\ \begin{array}{r}
2 x-2 y+z=1 \\
2(1)-2(2)+3=1 \\
2-4+3=1 \\
-2+3=1 \\
1=1 \\
\text { TRUE }
\end{array}\)
Since \(\ x=1\), \(\ y=2\), and \(\ z=3\) is a solution for all three equations, it’s the solution for the system of equations. Just as two values can be written as an ordered pair, three values can be written as an ordered triplet: .
- Choose two equations and use them to eliminate one variable.
- Choose another pair of equations and use them to eliminate the same variable.
- Use the resulting pair of equations from steps 1 and 2 to eliminate one of the two remaining variables.
- Solve the final equation for the remaining variable.
- Find the value of the second variable. Do this by using one of the resulting equations from steps 1 and 2 and the value of the found variable from step 4.
- Find the value of the third variable. Do this by using one of the original equations and the values of the found variables from steps 4 and 5.
- Check your answer in all three equations!
Solve for \(\ f\), \(\ g\), and \(\ h\).
\(\ \begin{array}{r}
f+g+h&=&13 \\
f-h&=&-2 \\
-2 f+g&=&3
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
f+g+h &=&13 \\
f \ \ \ \ \ \ \ -h&=&-2 \\
\hline 2 f\ \ \ \ \ \ \ \ +g &=&11
\end{array}\)Step 1: Choose two equations and eliminate a variable. The first two equations can be added to eliminate \(\ h\). \(\ \begin{array}{r}
2 f+g&=&11 \\
-2 f+g&=&3
\end{array}\)Step 2: The third equation has no \(\ h\) variable, so there’s nothing to eliminate! You have a system of two equations and two variables. \(\ \begin{array}{r}
2 f+\ g&=&11 \\
-2 f+\ g&=&3 \\
\hline 2 g&=&14
\end{array}\)Step 3: Eliminate a second variable. These equations can be added to eliminate \(\ f\). \(\ \begin{array}{c}
2 g=14 \\
g=7
\end{array}\)Step 4: Solve the resulting equation for the remaining variable. \(\ \begin{array}{r}
2 f+g&=&11 \\
2 f+7&=&11 \\
2 f\ \ \ \ \ \ \ &=&4 \\
f\ \ \ \ \ \ \ &=&2
\end{array}\)Step 5: Use that value and one of the equations from the system in step 3 that involves just two variables, one of which was \(\ g\) that you already know. Solve for the second variable. \(\ \begin{array}{r}
f+g+h=13 \\
2+7+h=13 \\
9+h=13 \\
h=\ \ 4
\end{array}\)Step 6: Use the two found values and one of the original equations that had all three variables to solve for the third variable. \(\ \begin{array}{c}
f+g+h=13 \\
2+7+4=13 \\
9+4=13 \\
13=13 \\
\text { TRUE }
\end{array}\)\(\ \begin{array}{l}
f-h=-2\\
2-4=-2\\
-2=-2\\
\text { TRUE }
\end{array}\)\(\ \begin{array}{c}
-2 f+g=3 \\
-2(2)+7=3 \\
-4+7=3 \\
3=3 \\
\text { TRUE }
\end{array}\)Step 7: Check your answer. The solution is \(\ (f, g, h)=(2,7,4)\).
As with systems of two equations with two variables, you may need to add the opposite of one of the equations or even multiply one of the equations before adding in order to eliminate one of the variables.
Solve for \(\ x\), \(\ y\), and \(\ z\).
\(\ \begin{array}{r}
3 x-2 y+\ \ z=\ 12 \\
x+3 y+\ \ z=-4 \\
2 x+2 y-4 z=\ \ \ 6
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
3 x-2 y+z\ &=&12 \\
-1(x+3 y+z)&=&-1(-4) \\
\hline
\end{array}\)Step 1: First, choose two equations and eliminate a variable. Multiply the second equation by -1, and then add it to the first equation. This will eliminate \(\ z\). \(\ \begin{array}{r}
2 x+2 y-4 z&=&6 \\
4(x+3 y+z)&=&4(-4) \\
\hline
\end{array}\)\(\ \begin{array}{r}
2 x +\ \ 2 y-4 z&= & 6 \\
4 x+12 y+4 z&= & -16 \\
\hline 6 x+14 y\ \ \ \ \ \ \ \ \ & =&-10
\end{array}\)Step 2: Next, combine the third equation and one of the first two to eliminate \(\ z\) again. However, the third equation has a coefficient of -4 on \(\ z\) while the coefficients in the first two equations are both 1. So, multiply the second equation by 4 and add. \(\ \begin{array}{rr}
2 x-\ \ 5 y&= & 16 \\
6 x+14 y&= & -10 \\
\hline
\end{array}\)Step 3: Eliminate a second variable using the equations from steps 1 and 2. Again, they cannot be added as they are. Look at the coefficients on \(\ x\). If you multiply the equation from step 1 by -3, the \(\ x\) terms will have the same coefficient. \(\ \begin{array}{r}
-3(2 x-5 y)=-3(16) \\
6 x+14 y=\quad-10 \\
\hline
\end{array}\)\(\ \begin{array}{rlr}
-6 x+ & 15 y= & -48 \\
6 x+ & 14 y= & -10 \\
\hline & 29 y= & -58
\end{array}\)Multiply and then add. Be careful of the signs! \(\ \begin{array}{r}
29 y&=&-58 \\
y&=& -2
\end{array}\)Step 4: Solve the resulting equation for the remaining variable. \(\ \begin{array}{c}
2 x-5 y=16 \\
2 x-5(-2)=16 \\
2 x+10=16 \\
2 x=6 \\
x=3
\end{array}\)Step 5: Use that value and one of the equations from the system in step 3, that involves just two variables, one of which was \(\ y\). Solve for the second variable. \(\ \begin{array}{c}
x+3 y+z=-4 \\
3+3(-2)+z=-4 \\
3+(-6)+z=-4 \\
-3+z=-4 \\
z=-1
\end{array}\)Step 6: Use the two found values and one of the original equations to solve for the third variable. \(\ \begin{array}{c}
3 x-2 y+z=12 \\
3(3)-2(-2)+(-1)=12 \\
9+4-1=12 \\
13-1=12 \\
12=12 \\
\text { TRUE }
\end{array}\)\(\ \begin{array}{c}
x+3 y+z=-4 \\
3+3(-2)+(-1)=-4 \\
3+(-6)+(-1)=-4 \\
-3+(-1)=-4 \\
-4=-4 \\
\text { TRUE }
\end{array}\)\(\ \begin{array}{c}
2 x+2 y-4 z=6 \\
2(3)+2(-2)-4(-1)=6 \\
6+(-4)+4=6 \\
2+4=6 \\
6=6 \\
\text { TRUE }
\end{array}\)Step 7: Check your answer. The solution is \(\ (x, y, z)=(3,-2,-1)\).
These systems can be helpful for solving real-world problems.
Andrea sells photographs at art fairs. She prices the photos according to size: small photos cost $10, medium photos cost $15, and large photos cost $40. She usually sells as many small photos as medium and large photos combined. She also sells twice as many medium photos as large. A booth at the art fair costs $300.
If her sales go as usual, how many of each size photo must she sell to pay for the booth?
- Solution
-
\(\ S\)=number of small photos sold
\(\ M\)=number of medium photos sold
\(\ L\)=number of large photos sold
\(\ 10S\)=money received for small photos
\(\ 15M\)=money received for medium photos
\(\ 40L\)=money received for large photos
To set up the system, first choose the variables. In this case the unknown values are the number of small, medium, and large photos.
The total of her sales must be $300 to pay for the booth.
\(\ 10 S+15 M+40 L=300\)
\(\ S=M+L\)
\(\ M=2 L\)
The number of small photos is the same as the total of medium and large photos.
She sells twice as many medium photos as large photos.
\(\ \begin{array}{c}
10 S+15 M+40 L=300 \\
S-M-L=0 \\
M-2 L=0
\end{array}\)To make things easier, rewrite the equations to be in the same format, with all variables on the left side of the equal sign and only a constant number on the right.
Now solve the system.
\(\ \begin{array}{r}
10 S+15 M+40 L&=&300 \\
S-\ \ \ \ M-\quad L&=&0 \\
\hline
\end{array}\)\(\ \begin{array}{r}
10 S+15 M+40 L\ &=&300 \\
-10(S-\ \ \ \ M-\ \ \ L)&=&10(0)
\end{array}\)Step 1: First choose two equations and eliminate a variable. Since one equation has no \(\ S\) variable, it may be helpful to use the other two equations and eliminate the \(\ S\) variable from them. \(\ \begin{array}{r}
10 S+15 M+40 L&=&300 \\
-10 S+10 M+10 L&=&0 \\
\hline 25 M+50 L&=&300
\end{array}\)Multiply the second equation by -10 and add. \(\ M-2 L=0\) Step 2: The second equation for our two-variable system will be the remaining equation (that has no \(\ S\) variable). \(\ \begin{array}{r}
25 M+50 L&=&300 \\
M-\ \ 2 L&=&0 \\
\hline
\end{array}\)Step 3: Eliminate a second variable using the equations from steps 1 and 2. \(\ \begin{array}{r}
M+2 L &=12 \\
M-2 L &=\ \ 0 \\
\hline 2 M\ \ \ \ \ \ \ \ \ \ &=12
\end{array}\)While you could multiply the second equation by 25 to eliminate \(\ L\), the numbers will be easier to work with if you divide the first equation by 25. Don’t forget to be careful of the signs! \(\ \begin{array}{c}
2 M=12 \\
M=6
\end{array}\)Step 4: Solve the resulting equation for the remaining variable. \(\ \begin{aligned}
M&=2 L \\
6&=2 L \\
3&=L
\end{aligned}\)Step 5: Use that value and one of the equations containing just two variables, one of those variables being \(\ L\), that you already know, to solve for the second variable.t’s best to use one of the original equations—in case an error was made in multiplication. \(\ \begin{array}{c}
S=M+L \\
S=6+3 \\
S=9
\end{array}\)Step 6: Use the two found values and one of the original equations to solve for the third variable.
You can even use one of the equations before you rewrote it for the system.
She usually sells as many small photos as medium and large photos combined.
Medium and large photos combined \(\ =6+3=9\), which is the number of small photos.
She also sells twice as many medium photos as large.
Medium photos is 6, which is twice the number of large photos (3).
Step 7: Check your answer.
With application problems, it’s sometimes easier (and better) to use the original wording of the problem rather than the equations you write.
A booth at the art fair costs $300. Andrea receives $10(9) or $90 for the 9 small photos, $15(6) or $90 for the 6 medium photos, and $40(3) or $120 for the large photos.
\(\ \$ 90+\$ 90+\$ 120=\$ 300\).
If Andrea sells small photos, medium photos, and large photos, she’ll receive exactly the amount of money needed to pay for the booth.
Systems with No Solutions or an Infinite Number of Solutions
Now let’s look at Case 2 (no solution) and Case 3 (an infinite number of solutions).
Since you will not graph these equations, as it is difficult to graph in three dimensions on a 2-dimensional sheet of paper, you will look at what happens when you try to solve systems with no solutions or an infinite number of solutions.
Let’s look at a system that has no solutions.
\(\ \begin{array}{r}
5 x-2 y+\ \ z=\ \ \ 3 \\
4 x-4 y-8 z=\ \ \ 2 \\
-x+\ \ y+2 z=-3
\end{array}\)
Suppose you wanted to solve this system, and you started with the last two equations. Multiply the third equation by 4 and add it to the second equation to eliminate \(\ x\).
\(\ \begin{array}{r}
4 x-4 y-8 z\ \ &=\ \ \ \ \ \ \ \ 2 \\
4(-x+\ \ y+2 z) &=4(-3)
\end{array}\)
\(\ \begin{array}{r}
4 x-4 y-8 z=\ \ \ \ \ 2 \\
-4 x+4 y+8 z=-12 \\
\hline 0=-10
\end{array}\)
In this case, the result is a false statement. This means there are no solutions to the two equations and therefore there can be no solutions for the system of three equations. If this occurs for any two of the three equations, then there is no solution for the system of equations.
Now let’s look at a system that has an infinite number of solutions.
\(\ \begin{array}{r}
x-2 y+\ \ z=\ \ \ 3 \\
-3 x+6 y-3 z=-9 \\
4 x-8 y+4 z=\ 12
\end{array}\)
For the first step, you would choose two equations and combine them to eliminate a variable. You can eliminate \(\ x\) by multiplying the first equation by 3 and adding to the second equation.
\(\ \begin{array}{r}
3(x-2 y+z)=\ 3(3) \\
-3 x+6 y-3 z=\ -9 \\
\hline
\end{array}\)
\(\ \begin{array}{r}
3 x-6 y+3 z=\ \ \ 9 \\
-3 x+6 y-3 z= -9 \\
\hline 0=\ \ \ 0
\end{array}\)
Notice that when the two equations are added, all variables are eliminated! The final equation is a true statement: \(\ 0=0\).
When this happens, it’s because the two equations are equivalent. These two equations would graph as the same plane. But in order for the solution to the system of three equations to be infinite, you need to continue to check with the third equation.
Since the first two equations are equivalent, the system of equations could be written with only two equations. Continue as before. Multiply the first equation by -4 and add the third equation.
\(\ 4 x-8 y+4 z=-12\)
\(\ \begin{array}{r}
-4 x+8 y-4 z= & -12 \\
4 x-8 y+4 z= & 12 \\
\hline 0= & 0
\end{array}\)
Again, the final equation is the true statement \(\ 0=0\). So the third equation is the same plane as the first two. Now you can confirm that there are an infinite number of solutions—all of the points that are on the plane that these three equations each describe.
This is one type of situation where there are an infinite number of solutions. There are others, which you will not examine at this time.
How many solutions does the following system of equations have?
\(\ \begin{array}{c}
x+y+z=2 \\
2 x+2 y+2 z=4 \\
-3 x-3 y-3 z=-6
\end{array}\)
- Solution
-
\(\ \begin{array}{rr}
-2(x+y+z)=-2(2) \\
2 x+2 y+2 z=\ \ \ \ \ \ \ \ 4 \\
\hline
\end{array}\)Multiply the first equation by -2 and then add that resulting equation to the second equation. \(\ \begin{array}{r}
-2 x-2 y-2 z =-4 \\
2 x+2 y+2 z =\ \ \ 4 \\
\hline 0 =\ \ \ 0
\end{array}\)\(\ 0=0\) is a true statement, which leads us to believe that you may have an infinite number of solutions. This outcome indicates that the first pair of equations is really the same equation. The values of \(\ x\), \(\ y\), and \(\ z\) that will make the first equation work will also work for the second. \(\ \begin{array}{r}
3(x+y+z)=\ 3(2) \\
-3 x-3 y-3 z=\ -6 \\
\hline
\end{array}\)Now add the third equation with the first. \(\ \begin{array}{r}
3 x+3 y+3 z=\ \ \ 6 \\
-3 x-3 y-3 z=-6 \\
\hline 0=\ \ \ 0
\end{array}\)Again, the result is another true statement. The first and third equations are the same. So you have three equations that will all graph as the same plane. There are an infinite number of solutions to this system.
Solve the following system of equations.
\(\ \begin{array}{c}
x-y-2 z=4 \\
4 x-4 y-z=2 \\
-x+y+2 z=-3
\end{array}\)
- Solution
-
\(\ \begin{array}{r}
-4(x-y-2 z)=-4(4) \\
4 x-4 y-8 z=\ \ \ \ \ \ \ \ 2 \\
\hline
\end{array}\)Compare the coefficients on the \(\ x\) terms. Multiply the first equation by -4 and then add that resulting equation to the second equation. \(\ \begin{array}{r}
-4 x+4 y+8 z =-16 \\
4 x-4 y-8 z =\ \ \ \ \ 2 \\
\hline 0 =-14
\end{array}\)Notice that a false statement is produced: \(\ 0=-14\). This means that there is no solution to this system of equations; you do not have to complete any further steps. The system has no solutions.


