2.7.8: Solving Quadratic Equations
- Page ID
- 74493
By the end of this section, you will be able to:
- Solve quadratic equations using the Quadratic Formula
- Use the discriminant to predict the number and type of solutions of a quadratic equation
- Identify the most appropriate method to use to solve a quadratic equation
Before you get started, take this readiness quiz.
- Evaluate \(b^{2}-4 a b\) when \(a=3\) and \(b=−2\).
If you missed this problem, review Example 1.21. - Simplify: \(\sqrt{108}\).
If you missed this problem, review Example 8.13. - Simplify: \(\sqrt{50}\).
If you missed this problem, review Example 8.76.
Solve Quadratic Equations Using the Quadratic Formula
When we solved quadratic equations in the last section by completing the square, we took the same steps every time. By the end of the exercise set, you may have been wondering ‘isn’t there an easier way to do this?’ The answer is ‘yes’. Mathematicians look for patterns when they do things over and over in order to make their work easier. In this section we will derive and use a formula to find the solution of a quadratic equation.
We have already seen how to solve a formula for a specific variable ‘in general’, so that we would do the algebraic steps only once, and then use the new formula to find the value of the specific variable. Now we will go through the steps of completing the square using the general form of a quadratic equation to solve a quadratic equation for \(x\).
We start with the standard form of a quadratic equation and solve it for \(x\) by completing the square.
| \(ax^2 + bx + c = 0, \quad a \ne 0\) | |
| Isolate the variable terms on one side. | \(ax^2 + bx \quad = -c\) |
| Make the coefficient of \(x^{2}\) equal to \(1\), by dividing by \(a\). | \(\dfrac{ax^2}{a} + \dfrac{b}{a}x \quad = -\dfrac{c}{a}\) |
| Simplify. | \(x^2+ \dfrac{b}{a}x \quad = -\dfrac{c}{a}\) |
| To complete the square, find \(\left(\dfrac{1}{2} \cdot \dfrac{b}{a}\right)^{2}\) and add it to both sides of the equation. | |
| \(\left(\dfrac{1}{2} \dfrac{b}{a}\right)^{2}=\dfrac{b^{2}}{4 a^{2}}\) | \(x^2 + \dfrac{b}{a}x +{\color{red}{\dfrac{b^2}{4a^2}}}{\color{black}{ = -\dfrac{c}{a}\,+\,}}{\color{red}{\dfrac{b^2}{4a^2}}}\) |
| The left side is a perfect square, factor it. | \(\left( x + \dfrac{b}{2a}\right)^2 = -\dfrac{c}{a}+\dfrac{b^2}{4a^2}\) |
| Find the common denominator of the right side and write equivalent fractions with the common denominator. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{c\cdot\color{red}{4a}}{a\cdot\color{red}{4a}}\) |
| Simplify. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2}{4a^2}-\dfrac{4ac}{4a^2}\) |
| Combine to one fraction. | \(\left( x + \dfrac{b}{2a}\right)^2 =\dfrac{b^2-4ac}{4a^2}\) |
| Use the square root property. | \(x + \dfrac{b}{2a}= \pm\sqrt{\dfrac{b^2-4ac}{4a^2}}\) |
| Simplify the radical. | \(x + \dfrac{b}{2a}= \pm\dfrac{\sqrt{b^2-4ac}}{2a}\) |
| Add \(-\dfrac{b}{2a}\) to both sides of the equation. | \(x = -\dfrac{b}{2a} \pm\dfrac{\sqrt{b^2-4ac}}{2a}\) |
| Combine the terms on the right side. | \(x = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\) |
The final equation is called the "Quadratic Formula."
The solutions to a quadratic equation of the form \(a x^{2}+b x+c=0\), where \(a≠0\) are given by the formula:
\[x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \label{quad}\]
To use the Quadratic Formula, we substitute the values of \(a,b\), and \(c\) from the standard form into the expression on the right side of the formula. Then we simplify the expression. The result is the pair of solutions to the quadratic equation.
Notice the Quadratic Formula (Equation \ref{quad}) is an equation. Make sure you use both sides of the equation.
Solve by using the Quadratic Formula: \(2 x^{2}+9 x-5=0\).
- Solution
-
Step 1: Write the quadratic equation in standard form. Identify the \(a,b,c\) values. This equation is in standard form. \(\begin{aligned} \color{red}{a x^{2}+b x+c =0} \\ 2 x^{2}+9 x-5 =0 \\ a=2, b =9, c=-5 \end{aligned}\) Step 2: Write the quadratic formula. Then substitute in the values of \(a,b,c\). Substitute in \(a=2, b=9, c=-5\) \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
\(x=\dfrac{-9 \pm \sqrt{9^{2}-4 \cdot 2 \cdot(-5)}}{2 \cdot 2}\)Step 3: Simplify the fraction, and solve for \(x\). \(\begin{array}{l}{x=\dfrac{-9 \pm \sqrt{81-(-40)}}{4}} \\ {x=\dfrac{-9 \pm \sqrt{121}}{4}} \\ {x=\dfrac{-9 \pm 11}{4}} \\ {x=\dfrac{-9+11}{4}}\quad x=\dfrac{-9-11}{4} \\ {x=\dfrac{2}{4} \quad \quad\:\:\: x=\dfrac{-20}{4}}\\ {x=\dfrac{1}{2} \quad\quad\:\:\: x=-5}\end{array}\) Step 4: Check the solutions. Put each answer in the original equation to check. Substitute \(x=\color{red}{\dfrac{1}{2}}\) and \(x=\color{red}{-5}\). \(\begin{aligned}2 x^{2}+9 x-5&=0 \\ 2\color{black}{\left(\color{red}{\dfrac{1}{2}}\right)}^{2}+9 \cdot \color{red}{\dfrac{1}{2}}\color{black}{-}5 &\stackrel{?}{=} 0 \\ 2\cdot\dfrac{1}{4}+0\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ 2\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{2}-5&\stackrel{?}{=}0 \\ \dfrac{1}{2}+\dfrac{9}{2}-5&\stackrel{?}{=}0 \\ \dfrac{10}{2}-5&\stackrel{?}{=}0 \\5-5&\stackrel{?}{=}0\\0&=0\end{aligned}\)
\(\begin{array}{r}{2 x^{2}+9 x-5=0} \\ {2(\color{red}{-5}\color{black}{)}^{2}+9(\color{red}{-5}\color{black}{)}-5\stackrel{?}{=}0} \\ {2 \cdot 25-45-5\stackrel{?}{=}0} \\ {50-45-5\stackrel{?}{=}0} \\ {0=0}\end{array}\)
- Write the quadratic equation in standard form, \(a x^{2}+b x+c=0\). Identify the values of \(a,b\), and \(c\).
- Write the Quadratic Formula. Then substitute in the values of \(a,b\), and \(c\).
- Simplify.
- Check the solutions.
If you say the formula as you write it in each problem, you’ll have it memorized in no time! And remember, the Quadratic Formula is an EQUATION. Be sure you start with “\(x=\)”.
Solve by using the Quadratic Formula: \(x^{2}-6 x=-5\).
- Solution
-
\(x^{2}-6 x=-5\)
Write the equation in standard form by adding \(5\) to each side. \(x^{2}-6 x+5=0\)
This equation is now in standard form. \({\color{red}{\small{ax^2+bx + c} = \small{0}}}\)
\(x^2 - 6x + 5 = 0\)Identify the values of \(\color{cyan}a\), \(\color{red}b\), \(\color{limegreen}c\). \({\color{cyan}a=1}\), \({\color{red}b=-6}\), \({\color{limegreen}c=5}\) Write the Quadratic Formula. \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Then substitute in the values of \(a, b, c\). \(x=\dfrac{-\color{red} (-6 ) \color{black} \pm \sqrt{\color{red}(-6) \color{black}^{2}-4 \cdot \color{cyan}1 \color{black} \cdot ( \color{limegreen}5 \color{black})}}{2 \cdot \color{cyan} 1} \)
Simplify. \(x=\dfrac{6 \pm \sqrt{36-20}}{2}\)
\(x=\dfrac{6 \pm \sqrt{16}}{2}\)
\(x=\dfrac{6 \pm 4}{2}\)
Rewrite to show two solutions. \(x=\frac{6+4}{2}, \quad x=\frac{6-4}{2}\)
Simplify. \(x=\frac{10}{2}, \quad x=\frac{2}{2}\)
\(x=5, \quad x=1\) Check:
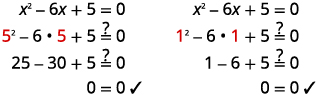
When we solved quadratic equations by using the Square Root Property, we sometimes got answers that had radicals. That can happen, too, when using the Quadratic Formula. If we get a radical as a solution, the final answer must have the radical in its simplified form.
Solve by using the Quadratic Formula: \(2 x^{2}+10 x+11=0\).
- Solution
-

This equation is in standard form. 
Identify the values of \(a,b\) and \(c\). 
Write the Quadratic Formula. \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
Then substitute in the values of \(a, b\), and \(c\). 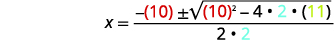
Simplify. \(x=\dfrac{-10 \pm \sqrt{100-88}}{4}\)
\(x=\dfrac{-10 \pm \sqrt{12}}{4}\)
Simplify the radical. \(x=\dfrac{-10 \pm 2 \sqrt{3}}{4}\)
Factor out the common factor in the numerator. 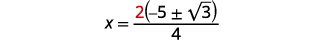
\(x=\dfrac{\color{red}{2}(-5 \pm \sqrt{3})}{4}\)
Remove the common factors. \(x=\dfrac{-5 \pm \sqrt{3}}{2}\)
Rewrite to show two solutions. \(x=\dfrac{-5+\sqrt{3}}{2}, \quad x=\dfrac{-5-\sqrt{3}}{2}\)
Check:
We leave the check for you!
When we substitute \(a, b\), and \(c\) into the Quadratic Formula and the radicand is negative, the quadratic equation will have imaginary or complex solutions. We will see this in the next example.
Solve by using the Quadratic Formula: \(3 p^{2}+2 p+9=0\).
- Solution
-

This equation is in standard form. 
Identify the values of \(a,b,c\). 
Write the Quadratic Formula. 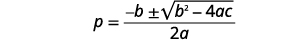
Then substitute in the values of \(a,b,c\). 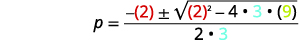
Simplify. 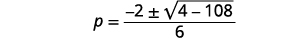
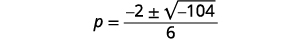
Simplify the radical using complex numbers. 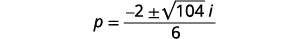
Simplify the radical. 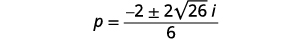
Factor the common factor in the numerator. 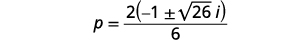
Remove the common factors. 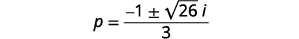
Rewrite in standard \(a+bi\) form. 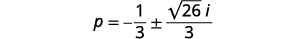
Write as two solutions. 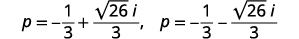
Table 9.3.5
Remember, to use the Quadratic Formula, the equation must be written in standard form, \(a x^{2}+b x+c=0\). Sometimes, we will need to do some algebra to get the equation into standard form before we can use the Quadratic Formula.
Solve by using the Quadratic Formula: \(x(x+6)+4=0\).
- Solution
-
Our first step is to get the equation in standard form.

Distribute to get the equation in standard form. 
This equation is now in standard form. 
Identify the values of \(a,b,c\). 
Write the Quadratic Formula. 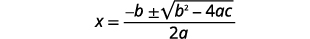
Then substitute in the values of \(a,b,c\). 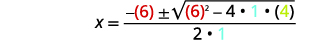
Simplify. 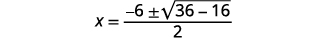
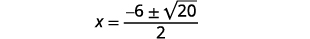
Simplify the radical. 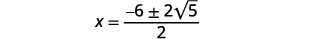
Factor the common factor in the numerator. 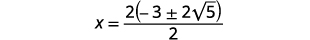
Remove the common factors. 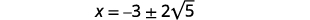
Write as two solutions. 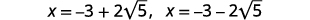
Check:
We leave the check for you!
Table 9.3.6
When we solved linear equations, if an equation had too many fractions we cleared the fractions by multiplying both sides of the equation by the LCD. This gave us an equivalent equation—without fractions— to solve. We can use the same strategy with quadratic equations.
Solve by using the Quadratic Formula: \(\dfrac{1}{2} u^{2}+\dfrac{2}{3} u=\dfrac{1}{3}\).
- Solution
-
Our first step is to clear the fractions.

Multiply both sides by the LCD, \(6\), to clear the fractions. 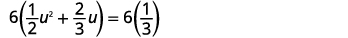
Multiply. 
Subtract \(2\) to get the equation in standard form. 
Identify the values of \(a, b\), and \(c\). 
Write the Quadratic Formula. 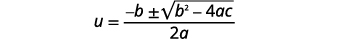
Then substitute in the values of \(a, b,\) and \(c\). 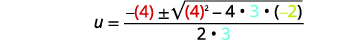
Simplify. 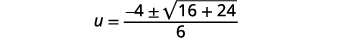
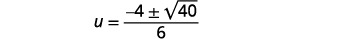
Simplify the radical. 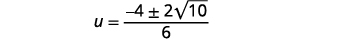
Factor the common factor in the numerator. 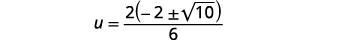
Remove the common factors. 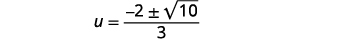
Rewrite to show two solutions. 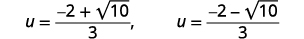
Check:
We leave the check for you!
Table 9.3.7
Think about the equation \((x-3)^{2}=0\). We know from the Zero Product Property that this equation has only one solution, \(x=3\).
We will see in the next example how using the Quadratic Formula to solve an equation whose standard form is a perfect square trinomial equal to \(0\) gives just one solution. Notice that once the radicand is simplified it becomes \(0\), which leads to only one solution.
Solve by using the Quadratic Formula: \(4 x^{2}-20 x=-25\).
- Solution
-

Add \(25\) to get the equation in standard form. 
Identify the values of \(a, b\), and \(c\). 
Write the quadratic formula. 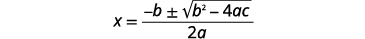
Then substitute in the values of \(a, b\), and \(c\). 
Simplify. 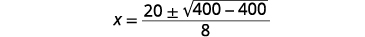
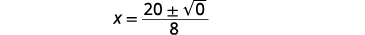
Simplify the radical. 
Simplify the fraction. 
Check:
We leave the check for you!
Table 9.3.8 Did you recognize that \(4 x^{2}-20 x+25\) is a perfect square trinomial. It is equivalent to \((2 x-5)^{2}\)? If you solve \(4 x^{2}-20 x+25=0\) by factoring and then using the Square Root Property, do you get the same result?
Use the Discriminant to Predict the Number and Type of Solutions of a Quadratic Equation
When we solved the quadratic equations in the previous examples, sometimes we got two real solutions, one real solution, and sometimes two complex solutions. Is there a way to predict the number and type of solutions to a quadratic equation without actually solving the equation?
Yes, the expression under the radical of the Quadratic Formula makes it easy for us to determine the number and type of solutions. This expression is called the discriminant.
Discriminant

Let’s look at the discriminant of the equations in some of the examples and the number and type of solutions to those quadratic equations.
| Quadratic Equation (in standard form) | Discriminat \(b^{2}-4ac\) | Value of the Discriminant | Number and Type of Solutions |
|---|---|---|---|
| \(2 x^{2}+9 x-5=0\) | \(\begin{aligned} 9^{2}-& 4 \cdot 2(-5) \\ & 121 \end{aligned}\) | \(+\) | \(2\) real |
| \(4 x^{2}-20 x+25=0\) | \((-20)^{2}-4 \cdot 4 \cdot 25\) \(0\) |
\(0\) | \(1\) real |
| \(3 p^{2}+2 p+9=0\) | \(2^{2}-4 \cdot 3 \cdot 9\) \(-104\) |
\(-\) | \(2\) complex |

Using the Discriminant \(b^{2}-4ac\), to Determine the Number and Type of Solutions of a Quadratic Equation
For a quadratic equation of the form \(ax^{2}+bx+c=0\), \(a \neq 0\),
- If \(b^{2}-4 a c>0\), the equation has \(2\) real solutions.
- if \(b^{2}-4 a c=0\), the equation has \(1\) real solution.
- if \(b^{2}-4 a c<0\), the equation has \(2\) complex solutions.
Determine the number of solutions to each quadratic equation.
- \(3 x^{2}+7 x-9=0\)
- \(5 n^{2}+n+4=0\)
- \(9 y^{2}-6 y+1=0\)
- Solution
-
To determine the number of solutions of each quadratic equation, we will look at its discriminant.
a.
\(3 x^{2}+7 x-9=0\)
The equation is in standard form, identify \(a, b\), and \(c\).
\(a=3, \quad b=7, \quad c=-9\)
Write the discriminant.
\(b^{2}-4 a c\)
Substitute in the values of \(a, b\), and \(c\).
\((7)^{2}-4 \cdot 3 \cdot(-9)\)
Simplify.
\(49+108\)
\(157\)Since the discriminant is positive, there are \(2\) real solutions to the equation.
b.
\(5 n^{2}+n+4=0\)
The equation is in standard form, identify \(a, b\), and \(c\).
\(a=5, \quad b=1, \quad c=4\)
Write the discriminant.
\(b^{2}-4 a c\)
Substitute in the values of \(a, b\), and \(c\).
\((1)^{2}-4 \cdot 5 \cdot 4\)
Simplify.
\(1-80\)
\(-79\)Since the discriminant is negative, there are \(2\) complex solutions to the equation.
c.
\(9 y^{2}-6 y+1=0\)
The equation is in standard form, identify \(a, b\), and \(c\).
\(a=9, \quad b=-6, \quad c=1\)
Write the discriminant.
\(b^{2}-4 a c\)
Substitute in the values of \(a, b\), and \(c\).
\((-6)^{2}-4 \cdot 9 \cdot 1\)
Simplify.
\(36-36\)
\(0\)Since the discriminant is \(0\), there is \(1\) real solution to the equation.
Identify the Most Appropriate Method to Use to Solve a Quadratic Equation
We summarize the four methods that we have used to solve quadratic equations below.
Methods for Solving Quadratic Equations
- Factoring
- Square Root Property
- Completing the Square
- Quadratic Formula
Given that we have four methods to use to solve a quadratic equation, how do you decide which one to use? Factoring is often the quickest method and so we try it first. If the equation is \(ax^{2}=k\) or \(a(x−h)^{2}=k\) we use the Square Root Property. For any other equation, it is probably best to use the Quadratic Formula. Remember, you can solve any quadratic equation by using the Quadratic Formula, but that is not always the easiest method.
What about the method of Completing the Square? Most people find that method cumbersome and prefer not to use it. We needed to include it in the list of methods because we completed the square in general to derive the Quadratic Formula. You will also use the process of Completing the Square in other areas of algebra.
Identify the Most Appropriate Method to Solve a Quadratic Equation
- Try Factoring first. If the quadratic factors easily, this method is very quick.
- Try the Square Root Property next. If the equation fits the form \(ax^{2}=k\) or \(a(x−h)^{2}=k\), it can easily be solved by using the Square Root Property.
- Use the Quadratic Formula. Any other quadratic equation is best solved by using the Quadratic Formula.
The next example uses this strategy to decide how to solve each quadratic equation.
Identify the most appropriate method to use to solve each quadratic equation.
- \(5 z^{2}=17\)
- \(4 x^{2}-12 x+9=0\)
- \(8 u^{2}+6 u=11\)
- Solution
-
a.
\(5z^{2}=17\)
Since the equation is in the \(ax^{2}=k\), the most appropriate method is to use the Square Root Property.
b.
\(4 x^{2}-12 x+9=0\)
We recognize that the left side of the equation is a perfect square trinomial, and so factoring will be the most appropriate method.
c.
\(8 u^{2}+6 u=11\)
Put the equation in standard form.
\(8 u^{2}+6 u-11=0\)
While our first thought may be to try factoring, thinking about all the possibilities for trial and error method leads us to choose the Quadratic Formula as the most appropriate method.
Problems Involving the Quadratic Formula
First comes the quadratic equation, then comes the quadratic formula. The quadratic formula is the solution to the quadratic equation:
\[ax^2+bx+c=0\]
in which
x is the variable whose value is sought, and a, b, and c are constants
The goal is to find the value of x that makes the left side 0. That value is given by the quadratic formula:
\[x=\dfrac{-b\pm\sqrt {b^2-4ac}}{2a}\]
to be read/said:
‘x’ equals minus ‘b’, plus-or-minus the square root of ‘b’ squared minus four ‘a’ ‘c’, all over two ‘a’.
So, how do you know when you have to use the quadratic formula? There is a good chance that you need it when the square of the variable for which you are solving, appears in the equation you are solving. When that is the case, carry out the algebraic steps needed to arrange the terms as they are arranged in equation 1-8 above. If this is impossible, then the quadratic formula is not to be used. Note that in the quadratic equation you have a term with the variable to the second power, a term with the variable to the first power, and a term with the variable to the zeroth power (the constant term). If additional powers also appear, such as the one-half power (the square root), or the third power, then the quadratic formula does not apply. If the equation includes additional terms in which the variable whose value is sought appears as the argument of a special function such as the sine function or the exponential function, then the quadratic formula does not apply. Now suppose that there is a square term and you can get the equation that you are solving in the form of equation 1-8 above but that either b or c is zero. In such a case, you can use the quadratic formula, but it is overkill. If b in equation 1-8 above is zero then the equation reduces to:
\[ax^2+bx=0\]
The easy way to solve this problem is to recognize that there is at least one x in each term, and to factor the x out. This yields:
\[(ax+b)x=0\]
Then you have to realize that a product of two multiplicands is equal to zero if either multiplicand is equal to zero. Thus, setting either multiplicand equal to zero and solving for x yields a solution. We have two multiplicands involving x, so, there are two solutions to the equation. The second multiplicand in the expression \((ax+b)x=0\) is x itself, so
\[x=0\]
is a solution to the equation. Setting the first term equal to zero gives:
\[ax+b=0\]
\[ax=-b\]
\[x=-\dfrac{b}{a}\]
Now suppose the b in the quadratic equation \(ax^2+bx+c=0\), equation 1-8, is zero. In that case, the quadratic equation reduces to:
\[ax^2+c=0\]
which can easily be solved without the quadratic formula as follows:
\[ax^2=-c\]
\[x^2=-\dfrac{c}{a}\]
\[x=\pm\sqrt {-\dfrac{c}{a}}\]
where we have emphasized the fact that there are two square roots to every value by placing a plus-or-minus sign in front of the radical.
Now, if upon arranging the given equation in the form of the quadratic equation (equation 1-8):\[ax^2+bx+c=0\]
you find that a, b, and c are all non-zero, then you should use the quadratic formula. Here we present an example of a problem whose solution involves the quadratic formula:
Given \[3+x=\dfrac{24}{x+1}\] find x.
Solution
At first glance, this one doesn’t look like a quadratic equation, but as we begin isolating x, as we always strive to do in solving for x, (hey, once we have x all by itself on the left side of the equation, with no x on the right side of the equation, we have indeed solved for x—that’s what it means to solve for x) we quickly find that it is a quadratic equation. Whenever we have the unknown in the denominator of a fraction, the first step in isolating that unknown is to multiply both sides of the equation by the denominator. In the case at hand, this yields:
\[(x+1)(x+3)=24\]
Multiplying through on the left we find
\[3x+3+x^2+x=24\]
At this point it is pretty clear that we are dealing with a quadratic equation so our goal becomes getting it into the standard form of the quadratic equation, the form of equation 1-8, namely: \(ax^2+bx+c=0\). Combining the terms involving x on the left and rearranging we obtain \[x^2+4x+3=24\]
Subtracting 24 from both sides yields:
\[x^2+4x-21=0\]
which is indeed in the standard quadratic equation form. Now we just have to use inspection to identify which values in our given equation are the a, b, and c that appear in the standard quadratic equation (equation 1-8) \(ax^2+bx+c=0\). Although it is not written, the constant multiplying the x2, in the case at hand, is just 1. So we have a = 1, b = 4, and c = −21.
Substituting these values into the quadratic formula (equation 1-9):\[x=\dfrac{-b\pm\sqrt {b^2-4ac}}{2a}\]
yields
\[x=\dfrac{-4\pm\sqrt {4^2-4(1)(21)}}{2(1)}\]
which results in x=3,x=-7
as the solutions to the problem. As a quick check we substitute each of these values back into the original equation:
\[3+x=\dfrac{24}{x+1}\]
and find that each substitution leads to an identity. (An identity is an equation whose validity is trivially obvious, such as 6 = 6.)
Key Concepts
- Quadratic Formula
- The solutions to a quadratic equation of the form \(a x^{2}+b x+c=0, a \neq 0\) are given by the formula:
\(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
- The solutions to a quadratic equation of the form \(a x^{2}+b x+c=0, a \neq 0\) are given by the formula:
- How to solve a quadratic equation using the Quadratic Formula.
- Write the quadratic equation in standard form, \(a x^{2}+b x+c=0\). Identify the values of \(a, b, c\).
- Write the Quadratic Formula. Then substitute in the values of \(a, b, c\).
- Simplify.
- Check the solutions.
- Using the Discriminant, \(b^{2}-4 a c\), to Determine the Number and Type of Solutions of a Quadratic Equation
- For a quadratic equation of the form \(a x^{2}+b x+c=0, a \neq 0\),
- If \(b^{2}-4 a c>0\), the equation has \(2\) real solutions.
- If \(b^{2}-4 a c=0\), the equation has \(1\) real solution.
- If \(b^{2}-4 a c<0\), the equation has \(2\) complex solutions.
- For a quadratic equation of the form \(a x^{2}+b x+c=0, a \neq 0\),
- Methods to Solve Quadratic Equations:
- Factoring
- Square Root Property
- Completing the Square
- Quadratic Formula
- How to identify the most appropriate method to solve a quadratic equation.
- Try Factoring first. If the quadratic factors easily, this method is very quick.
- Try the Square Root Property next. If the equation fits the form \(a x^{2}=k\) or \(a(x-h)^{2}=k\), it can easily be solved by using the Square Root Property.
- Use the Quadratic Formula. Any other quadratic equation is best solved by using the Quadratic Formula.
Glossary
- discriminant
- In the Quadratic Formula, \(x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\), the quantity \(b^{2}-4 a c\) is called the discriminant.


