2.7.15: Derivatives
- Page ID
- 74889
- Recognize the meaning of the tangent to a curve at a point.
- Calculate the slope of a tangent line.
- Identify the derivative as the limit of a difference quotient.
- Calculate the derivative of a given function at a point.
- Describe the velocity as a rate of change.
- Explain the difference between average velocity and instantaneous velocity.
- Estimate the derivative from a table of values.
Tangent Lines
We define the tangent line to the graph of a function as follows.
Let \(f(x)\) be a function defined in an open interval containing \(a\). The tangent line to \(f(x)\) at \(a\) is the line passing through the point \((a,f(a))\) having slope
\[m_{tan}=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \label{tanline1}\]
provided this limit exists.
Equivalently, we may define the tangent line to \(f(x)\) at \(a\) to be the line passing through the point \((a,f(a))\) having slope
\[m_{tan}=\lim_{h→0}\frac{f(a+h)−f(a)}{h} \label{tanline2}\]
provided this limit exists.
Find the equation of the line tangent to the graph of \(f(x)=x^2\) at \(x=3.\)
- Solution
-
First find the slope of the tangent line. In this example, use Equation \ref{tanline1}.
\(\displaystyle \begin{align*} m_{tan}&=\lim_{x→3}\frac{f(x)−f(3)}{x−3} & & \text{Apply the definition.}\\[4pt]
&=\lim_{x→3}\frac{x^2−9}{x−3} & & \text{Substitute }f(x)=x^2\text{ and }f(3)=9\\[4pt]
&=\lim_{x→3}\frac{(x−3)(x+3)}{x−3} =\lim_{x→3}(x+3)=6 & & \text{Factor the numerator to evaluate the limit.}\end{align*}\)Next, find a point on the tangent line. Since the line is tangent to the graph of \(f(x)\) at \(x=3\), it passes through the point \((3,f(3))\). We have \(f(3)=9\), so the tangent line passes through the point \((3,9)\).
Using the point-slope equation of the line with the slope \(m=6\) and the point \((3,9)\), we obtain the line \(y−9=6(x−3)\). Simplifying, we have \(y=6x−9\). The graph of \(f(x)=x^2\) and its tangent line at \(3\) are shown in Figure \(\PageIndex{5}\).
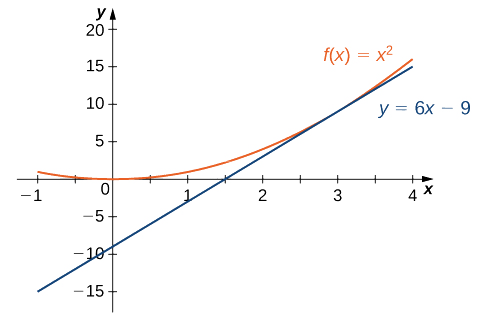
Figure \(\PageIndex{5}\): The tangent line to \(f(x)\) at \(x=3\).
Use Equation \ref{tanline2} to find the slope of the line tangent to the graph of \(f(x)=x^2\) at \(x=3\).
- Solution
-
The steps are very similar to Example \(\PageIndex{1}\). See Equation \ref{tanline2} for the definition.
\(\begin{align*} m_{tan}&=\lim_{h→0}\frac{f(3+h)−f(3)}{h} & & \text{Apply the definition.}\\[4pt]
&=\lim_{h→0}\frac{(3+h)^2−9}{h} & & \text{Substitute }f(3+h)=(3+h)^2\text{ and }f(3)=9\\[4pt]
&=\lim_{h→0}\frac{9+6h+h^2−9}{h} & & \text{Expand and simplify to evaluate the limit.}\\[4pt]
&=\lim_{h→0}\frac{h(6+h)}{h}=\lim_{h→0}(6+h)=6 \end{align*}\)We obtained the same value for the slope of the tangent line by using the other definition, demonstrating that the formulas can be interchanged.
Find the equation of the line tangent to the graph of \(f(x)=1/x\) at \(x=2\).
- Solution
-
We can use Equation \ref{tanline1}, but as we have seen, the results are the same if we use Equation \ref{tanline2}.
\(\displaystyle \begin{align*} m_{tan}&=\lim_{x→2}\frac{f(x)−f(2)}{x−2} & & \text{Apply the definition.}\\[4pt]
&=\lim_{x→2}\frac{\frac{1}{x}−\frac{1}{2}}{x−2} & & \text{Substitute }f(x)=\frac{1}{x}\text{ and }f(2)=\frac{1}{2}\\[4pt]
&=\lim_{x→2}\frac{\frac{1}{x}−\frac{1}{2}}{x−2}⋅\frac{2x}{2x} & & \text{Multiply numerator and denominator by }2x\text{ to simplify fractions.}\\[4pt]
&=\lim_{x→2}\frac{(2−x)}{(x−2)(2x)} & & \text{Simplify.}\\[4pt]
&=\lim_{x→2}\frac{−1}{2x} & & \text{Simplify using }\frac{2−x}{x−2}=−1,\text{ for }x≠2.\\[4pt]
&=−\frac{1}{4} & & \text{Evaluate the limit.}\end{align*}\)We now know that the slope of the tangent line is \(−\frac{1}{4}\). To find the equation of the tangent line, we also need a point on the line. We know that \(f(2)=\frac{1}{2}\). Since the tangent line passes through the point \((2,\frac{1}{2})\) we can use the point-slope equation of a line to find the equation of the tangent line. Thus the tangent line has the equation \(y=−\frac{1}{4}x+1\). The graphs of \(f(x)=\frac{1}{x}\) and \(y=−\frac{1}{4}x+1\) are shown in Figure \(\PageIndex{6}\).
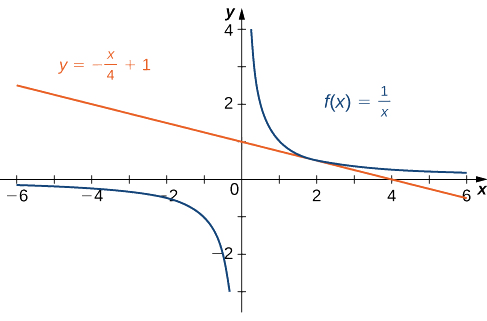
Figure \(\PageIndex{6}\):The line is tangent to \(f(x)\) at \(x=2\).
The Derivative of a Function at a Point
The type of limit we compute in order to find the slope of the line tangent to a function at a point occurs in many applications across many disciplines. These applications include velocity and acceleration in physics, marginal profit functions in business, and growth rates in biology. This limit occurs so frequently that we give this value a special name: the derivative. The process of finding a derivative is called differentiation.
Let \(f(x)\) be a function defined in an open interval containing \(a\). The derivative of the function \(f(x)\) at \(a\), denoted by \(f′(a)\), is defined by
\[f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a} \label{der1}\]
provided this limit exists.
Alternatively, we may also define the derivative of \(f(x)\) at \(a\) as
\[f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}. \label{der2}\]
For \(f(x)=x^2\), use a table to estimate \(f′(3)\) using Equation \ref{der1}.
- Solution
-
Create a table using values of \(x\) just below \(3\) and just above \(3\).
\(x\) \(\dfrac{x^2−9}{x−3}\) 2.9 5.9 2.99 5.99 2.999 5.999 3.001 6.001 3.01 6.01 3.1 6.1 After examining the table, we see that a good estimate is \(f′(3)=6\).
For \(f(x)=3x^2−4x+1\), find \(f′(2)\) by using Equation \ref{der1}.
- Solution
-
Substitute the given function and value directly into the equation.
\(\displaystyle \begin{align*} f′(x)&=\lim_{x→2}\frac{f(x)−f(2)}{x−2} & & \text{Apply the definition.}\\[4pt]
&=\lim_{x→2}\frac{(3x^2−4x+1)−5}{x−2} & & \text{Substitute }f(x)=3x^2−4x+1\text{ and }f(2)=5.\\[4pt]
&=\lim_{x→2}\frac{(x−2)(3x+2)}{x−2} & & \text{Simplify and factor the numerator.}\\[4pt]
&=\lim_{x→2}(3x+2) & & \text{Cancel the common factor.}\\[4pt]
&=8 & & \text{Evaluate the limit.}\end{align*}\)
For \(f(x)=3x^2−4x+1\), find \(f′(2)\) by using Equation \ref{der2}.
- Solution
-
Using this equation, we can substitute two values of the function into the equation, and we should get the same value as in Example \(\PageIndex{6}\).
\(\displaystyle \begin{align*} f′(2)&=\lim_{h→0}\frac{f(2+h)−f(2)}{h} & & \text{Apply the definition.}\\[4pt]
&=\lim_{h→0}\frac{(3(2+h)^2−4(2+h)+1)−5}{h} & & \text{Substitute }f(2)=5\text{ and }f(2+h)=3(2+h)^2−4(2+h)+1.\\[4pt]
&=\lim_{h→0}\frac{3(4+4h+h^2)-8-4h+1-5}{h} & & \text{Expand the numerator.}\\[4pt]
&=\lim_{h→0}\frac{12+12h+3h^2-12-4h}{h} & & \text{Distribute and begin simplifying the numerator.}\\[4pt]
&=\lim_{h→0}\frac{3h^2+8h}{h} & & \text{Finish simplifying the numerator.}\\[4pt]
&=\lim_{h→0}\frac{h(3h+8)}{h} & & \text{Factor the numerator.}\\[4pt]
&=\lim_{h→0}(3h+8) & & \text{Cancel the common factor.}\\[4pt]
&=8 & & \text{Evaluate the limit.} \end{align*} \)The results are the same whether we use Equation \ref{der1} or Equation \ref{der2}.
Velocities and Rates of Change
Now that we can evaluate a derivative, we can use it in velocity applications. Recall that if \(s(t)\) is the position of an object moving along a coordinate axis, the average velocity of the object over a time interval \([a,t]\) if \(t>a\) or \([t,a]\) if \(t<a\) is given by
\[v_{ave}=\frac{s(t)−s(a)}{t−a}. \label{avgvel}\]
As the values of \(t\) approach \(a\), the values of \(v_{ave}\) approach the value we call the instantaneous velocity at \(a\). That is, instantaneous velocity at \(a\), denoted \(v(a)\), is given by
\[v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}. \label{instvel}\]
To better understand the relationship between average velocity and instantaneous velocity, see Figure \(\PageIndex{7}\). In this figure, the slope of the tangent line (shown in red) is the instantaneous velocity of the object at time \(t=a\) whose position at time \(t\) is given by the function \(s(t)\). The slope of the secant line (shown in green) is the average velocity of the object over the time interval \([a,t]\).
We can use Equation \ref{instvel} to calculate the instantaneous velocity, or we can estimate the velocity of a moving object by using a table of values. We can then confirm the estimate by using Equation \ref{avgvel}.
A lead weight on a spring is oscillating up and down. Its position at time \(t\) with respect to a fixed horizontal line is given by \(s(t)=\sin t\) (Figure \(\PageIndex{8}\)). Use a table of values to estimate \(v(0)\). Check the estimate by using Equation \ref{instvel}.
- Solution
-
We can estimate the instantaneous velocity at \(t=0\) by computing a table of average velocities using values of \(t\) approaching \(0\), as shown in Table \(\PageIndex{2}\).
Table \(\PageIndex{2}\): Average velocities using values of \(t\) approaching 0 \(t\) \(\frac{\sin t−\sin 0}{t−0}=\frac{\sin t}{t}\) −0.1 0.998334166 −0.01 0.9999833333 −0.001 0.999999833 0.001 0.999999833 0.01 0.9999833333 0.1 0.998334166 From the table we see that the average velocity over the time interval \([−0.1,0]\) is \(0.998334166\), the average velocity over the time interval \([−0.01,0]\) is \(0.9999833333\), and so forth. Using this table of values, it appears that a good estimate is \(v(0)=1\).
By using Equation \ref{instvel}, we can see that
\[v(0)=s′(0)=\lim_{t→0}\frac{\sin t−\sin 0}{t−0}=\lim_{t→0}\frac{\sin t}{t}=1. \nonumber\]
Thus, in fact, \(v(0)=1\).
As we have seen throughout this section, the slope of a tangent line to a function and instantaneous velocity are related concepts. Each is calculated by computing a derivative and each measures the instantaneous rate of change of a function, or the rate of change of a function at any point along the function.
The instantaneous rate of change of a function \(f(x)\) at a value \(a\) is its derivative \(f′(a)\).
Reaching a top speed of \(270.49\) mph, the Hennessey Venom GT is one of the fastest cars in the world. In tests it went from \(0\) to \(60\) mph in \(3.05\) seconds, from \(0\) to \(100\) mph in \(5.88\) seconds, from \(0\) to \(200\) mph in \(14.51\) seconds, and from \(0\) to \(229.9\) mph in \(19.96\) seconds. Use this data to draw a conclusion about the rate of change of velocity (that is, its acceleration) as it approaches \(229.9\) mph. Does the rate at which the car is accelerating appear to be increasing, decreasing, or constant?
- Solution
- First observe that \(60\) mph = \(88\) ft/s, \(100\) mph ≈\(146.67\) ft/s, \(200\) mph ≈\(293.33\) ft/s, and \(229.9\) mph ≈\(337.19\) ft/s. We can summarize the information in a table.
Table \(\PageIndex{3}\): \(v(t)\) at different values of \(t\) \(t\) \(v(t)\) 0 0 3.05 88 5.88 147.67 14.51 293.33 19.96 337.19 Now compute the average acceleration of the car in feet per second on intervals of the form \([t,19.96]\) as \(t\) approaches \(19.96\), as shown in the following table.
Average acceleration \(t\) \(\dfrac{v(t)−v(19.96)}{t−19.96}=\dfrac{v(t)−337.19}{t−19.96}\) 0.0 16.89 3.05 14.74 5.88 13.46 14.51 8.05 The rate at which the car is accelerating is decreasing as its velocity approaches \(229.9\) mph (\(337.19\) ft/s).
A homeowner sets the thermostat so that the temperature in the house begins to drop from \(70°F\) at \(9\) p.m., reaches a low of \(60°\) during the night, and rises back to \(70°\) by \(7\) a.m. the next morning. Suppose that the temperature in the house is given by \(T(t)=0.4t^2−4t+70\) for \(0≤t≤10\), where \(t\) is the number of hours past \(9\) p.m. Find the instantaneous rate of change of the temperature at midnight.
- Solution
-
Since midnight is \(3\) hours past \(9\) p.m., we want to compute \(T′(3)\). Refer to Equation \ref{der1}.
\(\displaystyle \begin{align*} T′(3)&=\lim_{t→3}\frac{T(t)−T(3)}{t−3} & & \text{Apply the definition.}\\[4pt]
&=\lim_{t→3}\frac{0.4t^2−4t+70−61.6}{t−3} & & \text{Substitute }T(t)=0.4t^2−4t+70\text{ and }T(3)=61.6.\\[4pt]
&=\lim_{t→3}\frac{0.4t^2−4t+8.4}{t−3} & & \text{Simplify.}\\[4pt]
&=\lim_{t→3}\frac{0.4(t−3)(t−7)}{t−3}\\[4pt]
&=\lim_{t→3}0.4(t−7) & & \text{Cancel.}\\[4pt]
&=−1.6 & & \text{Evaluate the limit.} \end{align*}\)The instantaneous rate of change of the temperature at midnight is \(−1.6°F\) per hour.
A toy company can sell \(x\) electronic gaming systems at a price of \(p=−0.01x+400\) dollars per gaming system. The cost of manufacturing \(x\) systems is given by \(C(x)=100x+10,000\) dollars. Find the rate of change of profit when \(10,000\) games are produced. Should the toy company increase or decrease production?
- Solution
-
The profit \(P(x)\) earned by producing \(x\) gaming systems is \(R(x)−C(x)\), where \(R(x)\) is the revenue obtained from the sale of \(x\) games. Since the company can sell \(x\) games at \(p=−0.01x+400\) per game,
\(R(x)=xp=x(−0.01x+400)=−0.01x^2+400x\).
Consequently,
\(P(x)=−0.01x^2+300x−10,000\).
Therefore, evaluating the rate of change of profit gives
\(\displaystyle \begin{align*} P′(10000)&=\lim_{x→10000}\frac{P(x)−P(10000)}{x−10000}\\[4pt]
&=\lim_{x→10000}\frac{−0.01x^2+300x−10000−1990000}{x−10000}\\[4pt]
&=\lim_{x→10000}\frac{−0.01x^2+300x−2000000}{x−10000}\\[4pt]
&=100 \end{align*}\).Since the rate of change of profit \(P′(10,000)>0\) and \(P(10,000)>0\), the company should increase production.
Derivative
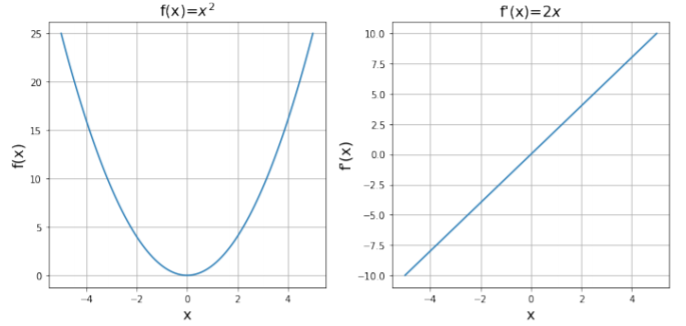
Consider the function \(f(x)=x^2\) that is plotted in Figure A2.1.1. For any value of \(x\), we can define the slope of the function as the “steepness of the curve”. For values of \(x>0\) the function increases as \(x\) increases, so we say that the slope is positive. For values of \(x<0\), the function decreases as \(x\) increases, so we say that the slope is negative. A synonym for the word slope is “derivative”, which is the word that we prefer to use in calculus. The derivative of a function \(f(x)\) is given the symbol \(\frac{df}{dx}\) to indicate that we are referring to the slope of \(f(x)\) when plotted as a function of \(x\).
We need to specify which variable we are taking the derivative with respect to when the function has more than one variable but only one of them should be considered independent. For example, the function \(f(x)=ax^2+b\) will have different values if \(a\) and \(b\) are changed, so we have to be precise in specifying that we are taking the derivative with respect to \(x\). The following notations are equivalent ways to say that we are taking the derivative of \(f(x)\) with respect to \(x\): \[\begin{aligned} \frac{df}{dx}=\frac{d}{dx} f(x) = f'(x) = f'\end{aligned}\] The notation with the prime (\(f'(x),f'\)) can be useful to indicate that the derivative itself is also a function of \(x\).
The slope (derivative) of a function tells us how rapidly the value of the function is changing when the independent variable is changing. For \(f(x)=x^2\), as \(x\) gets more and more positive, the function gets steeper and steeper; the derivative is thus increasing with \(x\). The sign of the derivative tells us if the function is increasing or decreasing, whereas its absolute value tells how quickly the function is changing (how steep it is).
We can approximate the derivative by evaluating how much \(f(x)\) changes when \(x\) changes by a small amount, say, \(\Delta x\). In the limit of \(\Delta x\to 0\), we get the derivative. In fact, this is the formal definition of the derivative:
\[\frac{df}{dx}=\lim_{\Delta x\to 0}\frac{\Delta f}{\Delta x}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\]
where \(\Delta f\) is the small change in \(f(x)\) that corresponds to the small change, \(\Delta x\), in \(x\). This makes the notation for the derivative more clear, \(dx\) is \(\Delta x\) in the limit where \(\Delta x\to0\), and \(df\) is \(\Delta f\), in the same limit of \(\Delta x\to 0\).
As an example, let us determine the function \(f'(x)\) that is the derivative of \(f(x)=x^2\). We start by calculating \(\Delta f\): \[\begin{aligned} \Delta f &= f(x+\Delta x)-f(x)\\ &=(x+\Delta x)^2 - x^2\\ &=x^2+2x\Delta x+\Delta x^2 -x^2\\ &=2x\Delta x+\Delta x^2\end{aligned}\] We now calculate \(\frac{\Delta f}{\Delta x}\): \[\begin{aligned} \frac{\Delta f}{\Delta x}&=\frac{2x\Delta x+\Delta x^2}{\Delta x}\\ &=2x+\Delta x\end{aligned}\] and take the limit \(\Delta x\to 0\): \[\begin{aligned} \frac{df}{dx}&=\lim_{\Delta x\to 0 }\frac{\Delta f}{\Delta x}\\ &=\lim_{\Delta x\to 0 }(2x+\Delta x)\\ &=2x\end{aligned}\] We have thus found that the function, \(f'(x)=2x\), is the derivative of the function \(f(x)=x^2\). This is illustrated in Figure A2.2.1. Note that:
- For \(x>0\), \(f'(x)\) is positive and increasing with increasing \(x\), just as we described earlier (the function \(f(x)\) is increasing and getting steeper).
- For \(x<0\), \(f'(x)\) is negative and decreasing in magnitude as \(x\) increases. Thus \(f(x)\) decreases and gets less steep as \(x\) increases.
- At \(x=0\), \(f'(x)=0\) indicating that, at the origin, the function \(f(x)\) is (momentarily) flat.
Common derivatives and properties
It is beyond the scope of this document to derive the functional form of the derivative for any function using Equation A2.2.1. Table A2.2.1 below gives the derivatives for common functions. In all cases, \(x\) is the independent variable, and all other variables should be thought of as constants:
| Function, \(f(x)\) | Derivative, \(f'(x)\) |
|---|---|
| \(f(x)=a\) | \(f'(x)=0\) |
| \(f(x)=x^n\) | \(f'(x)=nx^{n-1}\) |
| \(f(x)=\sin(x)\) | \(f'(x)=\cos(x)\) |
| \(f(x)=\cos(x)\) | \(f'(x)=-\sin(x)\) |
| \(f(x)=\tan(x)\) | \(f'(x)=\frac{1}{\cos^2(x)}\) |
| \(f(x)=e^x\) | \(f'(x)=e^x\) |
| \(f(x)=\ln(x)\) | \(f'(x)=\frac{1}{x}\) |
Table \(\PageIndex{3}\): Common derivatives of functions.
If two functions of 1 variable, \(f(x)\) and \(g(x)\), are combined into a third function, \(h(x)\), then there are simple rules for finding the derivative, \(h'(x)\), based on the derivatives \(f'(x)\) and \(g'(x)\). These are summarized in Table A2.2.2 below.
| Function, \(h(x)\) | Derivative, \(h'(x)\) |
|---|---|
| \(h(x)=f(x)+g(x)\) | \(h'(x)=f'(x)+g'(x)\) |
| \(h(x)=f(x)-g(x)\) | \(h'(x)=f'(x)-g'(x)\) |
| \(h(x)=f(x)g(x)\) | \(h'(x)=f'(x)g(x)+f(x)g'(x)\) (The product rule) |
| \(h(x)=\frac{f(x)}{g(x)}\) | \(h'(x)=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\) (The quotient rule) |
| \(h(x)=f(g(x))\) | \(h'(x)=f'(g(x))g'(x)\) (The Chain Rule) |
Table \(\PageIndex{4}\): Derivatives of combined functions.
Use the properties from Table A2.2.2 to show that the derivative of \(\tan(x)\) is \(\frac{1}{\cos^2(x)}\).
- Solution
-
Since \(\tan(x)=\frac{\sin(x)}{\cos(x)}\), we can write: \[\begin{aligned} h(x) &= \frac{f(x)}{g(x)} \\ f(x) &= \sin(x)\\ g(x) &= \cos(x)\end{aligned}\] Using the fourth row in Table A2.2.2, and the common derivatives from Table A2.2.1, we have: \[\begin{aligned} f'(x) &= \cos(x) \\ g'(x) &= -\sin(x) \\ g^2(x) &= \cos^2(x) \\ h'(x) &=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\\ &= \frac{\cos(x)\cos(x) - \sin(x) (-\sin(x))}{\cos^2}\\ &=\frac{\cos^2(x)+\sin^2(x)}{\cos^2}\\ &=\frac{1}{\cos^2(x)}\end{aligned}\] as required.
Use the properties from Table A2.2.2 to calculate the derivative of \(h(x)=\sin^2(x)\).
- Solution
-
To calculate the derivative of \(h(x)\), we need to use the Chain Rule. \(h(x)\) is found by first taking \(\sin(x)\) and then taking that result squared. We can thus identify: \[\begin{aligned} h(x) &= \sin^2(x) = f(g(x))\\ f(x) &= x^2 \\ g(x) &= \sin(x)\end{aligned}\] Using the common derivatives from Table A2.2.1, we have: \[\begin{aligned} f'(x) &= 2x \\ g'(x) &= \cos(x)\end{aligned}\] Applying the Chain Rule, we have: \[\begin{aligned} h'(x) &= f'(g(x))g'(x)\\ &= 2\sin(x)g'(x)\\ &= 2\sin(x)\cos(x)\end{aligned}\] where \(f'(g(x))\) means apply the derivative of \(f(x)\) to the function \(g(x)\). Since the derivative of \(f(x)\) is \(f'(x)=2x\), when we apply it to \(g(x)\) instead of \(2x\), we get \(2g(x)=2\cos(x)\).
Partial derivatives and gradients
So far, we have only looked at the derivative of a function of a single independent variable and used it to quantify how much the function changes when the independent variable changes. We can proceed analogously for a function of multiple variables, \(f(x,y)\), by quantifying how much the function changes along the direction associated with a particular variable. This is illustrated in Figure A2.2.2 for the function \(f(x,y)=x^2-2y^2\), which looks somewhat like a saddle.
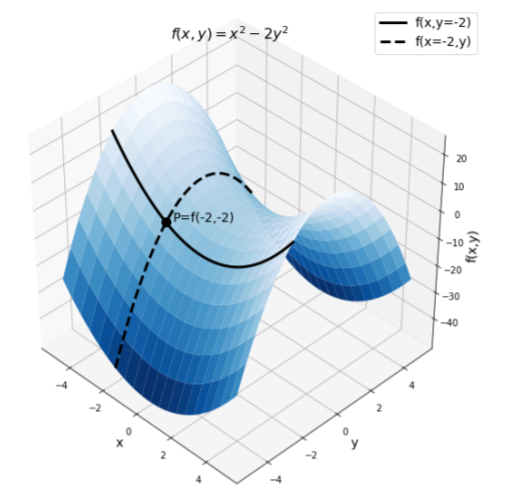
Suppose that we wish to determine the derivative of the function \(f(x)\) at \(x=-2\) and \(y=-2\). In this case, it does not make sense to simply determine the “derivative”, but rather, we must specify in which direction we want the derivative. That is, we need to specify in which direction we are interested in quantifying the rate of change of the function.
One possibility is to quantify the rate of change in the \(x\) direction. The solid line in Figure A2.2.2 shows the part of the function surface where \(y\) is fixed at -2, that is, the function evaluated as \(f(x,y=-2)\). The point \(P\) on the figure shows the value of the function when \(x=-2\) and \(y=-2\). By looking at the solid line at point \(P\), we can see that as \(x\) increases, the value of the function is gently decreasing. The derivative of \(f(x,y)\) with respect to \(x\) when \(y\) is held constant and evaluated at \(x=-2\) and \(y=-2\) is thus negative. Rather than saying “The derivative of \(f(x,y)\) with respect to \(x\) when \(y\) is held constant” we say “The partial derivative of \(f(x,y)\) with respect to \(x\)”.
Since the partial derivative is different than the ordinary derivative (as it implies that we are holding independent variables fixed), we give it a different symbol, namely, we use \(\partial\) instead of \(d\):
\[\begin{aligned}\frac{\partial f}{\partial x}=\frac{\partial}{\partial x}f(x,y)\quad\text{(Partial derivative of f with respect to x)}\end{aligned}\]
Calculating the partial derivative is very easy, as we just treat all variables as constants except for the variable with respect to which we are differentiating1. For the function \(f(x,y)=x^2-2y^2\), we have:
\[\begin{aligned} \frac{\partial f}{\partial x}&=\frac{\partial}{\partial x}(x^2-2y^2) = 2x\\ \frac{\partial f}{\partial y}&=\frac{\partial}{\partial y}(x^2-2y^2) = -4y\end{aligned}\]
At \(x=-2\), the partial derivative of \(f(x,y)\) is indeed negative, consistent with our observation that, along the solid line, at point \(P\), the function is decreasing.
A function will have as many partial derivatives as it has independent variables. Also note that, just like a normal derivative, a partial derivative is still a function. The partial derivative with respect to a variable tells us how steep the function is in the direction in which that variable increases and whether it is increasing or decreasing.
Determine the partial derivatives of \(f(x,y,z)=ax^2+byz-\sin(z)\).
- Solution
-
In this case, we have three partial derivatives to evaluate. Note that \(a\) are \(b\) constants and can be thought of as numbers that we do not know.
\[\begin{aligned} \frac{\partial f}{\partial x}&=\frac{\partial}{\partial x}(ax^2+byz-\sin(z)) = 2ax\\ \frac{\partial f}{\partial y}&=\frac{\partial}{\partial y}(ax^2+byz-\sin(z)) = bz \\ \frac{\partial f}{\partial z}&=\frac{\partial}{\partial z}(ax^2+byz-\sin(z)) = by-\cos(z) \end{aligned}\]
Since the partial derivatives tell us how the function changes in a particular direction, we can use them to find the direction in which the function changes the most rapidly. For example, suppose that the surface from Figure A2.2.2 corresponds to a real physical surface and that we place a ball at point \(P\). We wish to know in which direction the ball will roll. The direction that it will roll in is the opposite of the direction where \(f(x,y)\) increases the most rapidly (i.e. it will roll in the direction where \(f(x,y)\) decreases the most rapidly). The direction in which the function increases the most rapidly is called the “gradient” and denoted by \(\nabla f(x,y)\).
Since the gradient is a direction, it cannot be represented by a single number. Rather, we use a “vector” to indicate this direction. Since \(f(x,y)\) has two independent variables, the gradient will be a vector with two components. The components of the gradient are given by the partial derivatives: \[\begin{aligned} \nabla f(x,y) = \frac{\partial f}{\partial x}\hat x+\frac{\partial f}{\partial y} \hat y\end{aligned}\] where \(\hat x\) and \(\hat y\) are the unit vectors in the \(x\) and \(y\) directions, respectively (sometimes, the unit vectors are denoted \(\hat i\) and \(\hat j\)). The direction of the gradient tells us in which direction the function increases the fastest, and the magnitude of the gradient tells us how much the function increases in that direction.
Determine the gradient of the function \(f(x,y)=x^2-2y^2\) at the point \(x=-2\) and \(y=-2\).
- Solution
-
We have already found the partial derivatives that we need to evaluate at \(x=-2\) and \(y=-2\): \[\begin{aligned} \frac{\partial f}{\partial x}&= 2x\\ \frac{\partial f}{\partial y}&= -4y \\ \therefore \nabla f(x,y) &= \frac{\partial f}{\partial x}\hat x+\frac{\partial f}{\partial y} \hat y \\ &=2x\hat x-4y\hat y\end{aligned}\] Evaluating the gradient at \(x=-2\) and \(y=-2\): \[\begin{aligned} \nabla f(x,y) &= 2x\hat x-4y\hat y\\ &=-4 \hat x + 8 \hat y\\ &=4 (-\hat x+2\hat y)\\\end{aligned}\] The gradient vector points in the direction \((-1,2)\). That is, the function increases the most in the direction where you would take 1 pace in the negative \(x\) direction and 2 paces in the positive \(y\) direction. You can confirm this by looking at point \(P\) in Figure A2.2.2 and imagining in which direction you would have to go to climb the surface to get the steepest climb.
The gradient is itself a function, but it is not a real function (in the sense of a real number), since it evaluates to a vector. It is a mapping from real numbers \(x,y\) to a vector. As you take more advanced calculus courses, you will eventually encounter “vector calculus”, which is just the calculus for functions of multiple variables to which you were just introduced. The key point to remember here is that the gradient can be used to find the vector that points in the direction of maximal increase of the corresponding multi-variate function. This is precisely the quantity that we need in physics to determine in which direction a ball will roll when placed on a surface (it will roll in the direction opposite to the gradient vector).
Common uses of derivatives in physics
The simplest case of using a derivative is to describe the speed of an object. If an object covers a distance \(\Delta x\) in a period of time \(\Delta t\), it’s “average speed”, \(v_{avg}\), is defined as the distance covered by the object divided by the amount of time it took to cover that distance: \[\begin{aligned} v_{avg} = \frac{\Delta x}{\Delta t}\end{aligned}\] If the object changes speed (for example it is slowing down) over the distance \(\Delta x\), we can still define its “instantaneous speed”, \(v\), by measuring the amount of time, \(\Delta t\), that it takes the object to cover a very small distance, \(\Delta x\). The instantaneous speed is defined in the limit where \(\Delta x \to 0\): \[\begin{aligned} v = \lim_{\Delta x\to 0}\frac{\Delta x}{\Delta t}=\frac{dx}{dt}\end{aligned}\] which is precisely the derivative of \(x(t)\) with respect to \(t\). \(x(t)\) is a function that gives the position, \(x\), of the object along some \(x\) axis as a function of time. The speed of the object is thus the rate of change of its position.
Similarly, if the speed is changing with time, then we can define the “acceleration”, \(a\), of an object as the rate of change of its speed: \[\begin{aligned} a = \frac{dv}{dt}\end{aligned}\]
Footnotes
1. To take the derivative is to “differentiate”!
Key Takeaways
The derivative of a function, \(f(x)\), with respect to \(x\) can be written as: \[\begin{aligned} \frac{d}{dx} f(x)=\frac{df}{dx}=f'(x)\end{aligned}\] and measures the rate of change of the function with respect to \(x\). The derivative of a function is generally itself a function. The derivative is defined as: \[\begin{aligned} f'(x) = \lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\end{aligned}\] Graphically, the derivative of a function represents the slope of the function, and it is positive if the function is increasing, negative if the function is decreasing and zero if the function is flat. Derivatives can always be determined analytically for any continuous function.
A partial derivative measures the rate of change of a multi-variate function, \(f(x,y)\), with respect to one of its independent variables. The partial derivative with respect to one of the variables is evaluated by taking the derivative of the function with respect to that variable while treating all other independent variables as if they were constant. The partial derivative of a function (with respect to \(x\)) is written as: \[\begin{aligned} \frac{\partial f}{\partial x}\end{aligned}\] The gradient of a function, \(\nabla f(x,y)\), is a vector in the direction in which that function is increasing most rapidly. It is given by: \[\begin{aligned} \nabla f(x,y)=\frac{\partial f}{\partial x}\hat x + \frac{\partial f}{\partial y} \hat y\end{aligned}\]
Given a function, \(f(x)\), its anti-derivative with respect to \(x\), \(F(x)\), is written: \[\begin{aligned} F(x) = \int f(x) dx\end{aligned}\] \(F(x)\) is such that its derivative with respect to \(x\) is \(f(x)\): \[\begin{aligned} \frac{dF}{dx}=f(x)\end{aligned}\] The anti-derivative of a function is only ever defined up to a constant, \(C\). We usually write this as: \[\begin{aligned} \int f(x) dx = F(x) + C\end{aligned}\] since the derivative of \(F(x) +C\) will also be equal to \(f(x)\). The anti-derivative is also called the “indefinite integral” of \(f(x)\).
The definite integral of a function \(f(x)\), between \(x=a\) and \(x=b\), is written: \[\begin{aligned} \int_a^b f(x) dx\end{aligned}\] and is equal to the difference in the anti-derivative evaluated at \(x=a\) and \(x=b\): \[\begin{aligned} \int_a^b f(x) dx = F(b) - F(a)\end{aligned}\] where the constant \(C\) no longer matters, since it cancels out. Physical quantities only ever depend on definite integrals, since they must be determined without an arbitrary constant.
Definite integrals are very useful in physics because they are related to a sum. Given a function \(f(x)\), one can relate the sum of terms of the form \(f(x_i)\Delta x\) over a range of values from \(x=a\) to \(x=b\) to the integral of \(f(x)\) over that range: \[\begin{aligned} \lim_{\Delta x\to 0}\sum_{i=1}^{i=N} f(x_{i-1}) \Delta x = \int_{x_0}^{x_N}f(x) dx=F(x_N) - F(x_0)=\end{aligned}\]
Key Concepts
- The slope of the tangent line to a curve measures the instantaneous rate of change of a curve. We can calculate it by finding the limit of the difference quotient or the difference quotient with increment \(h\).
- The derivative of a function \(f(x)\) at a value \(a\) is found using either of the definitions for the slope of the tangent line.
- Velocity is the rate of change of position. As such, the velocity \(v(t)\) at time \(t\) is the derivative of the position \(s(t)\) at time \(t\).
Average velocity is given by \[v_{ave}=\dfrac{s(t)−s(a)}{t−a}. \nonumber\] Instantaneous velocity is given by \[\displaystyle v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}. \nonumber\] - We may estimate a derivative by using a table of values.
Key Equations
- Difference quotient
\(Q=\dfrac{f(x)−f(a)}{x−a}\)
- Difference quotient with increment h
\(Q=\dfrac{f(a+h)−f(a)}{a+h−a}=\dfrac{f(a+h)−f(a)}{h}\)
- Slope of tangent line
\(\displaystyle m_{tan}=\lim_{x→a}\frac{f(x)−f(a)}{x−a}\)
\(\displaystyle m_{tan}=\lim_{h→0}\frac{f(a+h)−f(a)}{h}\)
- Derivative of f(x) at a
\(\displaystyle f′(a)=\lim_{x→a}\frac{f(x)−f(a)}{x−a}\)
\(\displaystyle f′(a)=\lim_{h→0}\frac{f(a+h)−f(a)}{h}\)
- Average velocity
\(v_{ave}=\dfrac{s(t)−s(a)}{t−a}\)
- Instantaneous velocity
\(\displaystyle v(a)=s′(a)=\lim_{t→a}\frac{s(t)−s(a)}{t−a}\)