7.7: Calculating Moments of Inertia
- Page ID
- 68775
- Calculate the moment of inertia for uniformly shaped, rigid bodies
- Apply the parallel axis theorem to find the moment of inertia about any axis parallel to one already known
- Calculate the moment of inertia for compound objects
In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects (a skill that is critical for more advanced physics and engineering courses).
Moment of Inertia
We defined the moment of inertia I of an object to be
\[I = \sum_{i} m_i r_i^2 \]
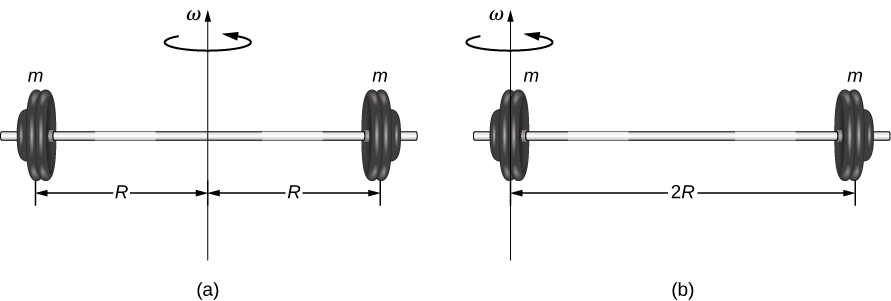
for all the point masses that make up the object. Because \(r\) is the distance to the axis of rotation from each piece of mass that makes up the object, the moment of inertia for any object depends on the chosen axis. To see this, let’s take a simple example of two masses at the end of a massless (negligibly small mass) rod (Figure \(\PageIndex{1}\)) and calculate the moment of inertia about two different axes. In this case, the summation over the masses is simple because the two masses at the end of the barbell can be approximated as point masses, and the sum therefore has only two terms.
In the case with the axis in the center of the barbell, each of the two masses m is a distance \(R\) away from the axis, giving a moment of inertia of
\[I_{1} = mR^{2} + mR^{2} = 2mR^{2} \ldotp\]
In the case with the axis at the end of the barbell—passing through one of the masses—the moment of inertia is
\[I_{2} = m(0)^{2} + m(2R)^{2} = 4mR^{2} \ldotp\]
From this result, we can conclude that it is twice as hard to rotate the barbell about the end than about its center.
In this example, we had two point masses and the sum was simple to calculate. However, to deal with objects that are not point-like, we need to think carefully about each of the terms in the equation. The equation asks us to sum over each ‘piece of mass’ a certain distance from the axis of rotation. But what exactly does each ‘piece of mass’ mean? Recall that in our derivation of this equation, each piece of mass had the same magnitude of velocity, which means the whole piece had to have a single distance r to the axis of rotation. However, this is not possible unless we take an infinitesimally small piece of mass dm, as shown in Figure \(\PageIndex{2}\).
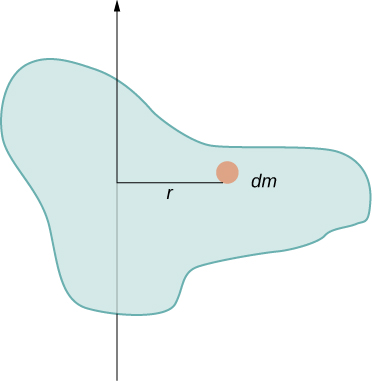
The need to use an infinitesimally small piece of mass dm suggests that we can write the moment of inertia by evaluating an integral over infinitesimal masses rather than doing a discrete sum over finite masses:
\[I = \sum_{i} m_{i} r_{i}^{2}\]
becomes
\[I = \int r^{2} dm \ldotp \label{10.19}\]
This, in fact, is the form we need to generalize the equation for complex shapes. It is best to work out specific examples in detail to get a feel for how to calculate the moment of inertia for specific shapes. This is the focus of most of the rest of this section.
A uniform thin rod with an axis through the center
Consider a uniform (density and shape) thin rod of mass M and length L as shown in Figure \(\PageIndex{3}\). We want a thin rod so that we can assume the cross-sectional area of the rod is small and the rod can be thought of as a string of masses along a one-dimensional straight line. In this example, the axis of rotation is perpendicular to the rod and passes through the midpoint for simplicity. Our task is to calculate the moment of inertia about this axis. We orient the axes so that the z-axis is the axis of rotation and the x-axis passes through the length of the rod, as shown in the figure. This is a convenient choice because we can then integrate along the x-axis.
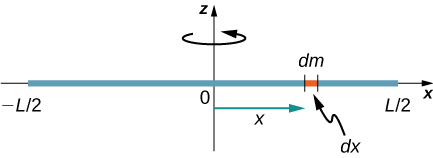
We define dm to be a small element of mass making up the rod. The moment of inertia integral is an integral over the mass distribution. However, we know how to integrate over space, not over mass. We therefore need to find a way to relate mass to spatial variables. We do this using the linear mass density \(\lambda\) of the object, which is the mass per unit length. Since the mass density of this object is uniform, we can write
\[\lambda = \frac{m}{l}\; or\; m = \lambda l \ldotp\]
If we take the differential of each side of this equation, we find
\[dm = d(\lambda l) = \lambda (dl)\]
since \(\lambda\) is constant. We chose to orient the rod along the x-axis for convenience—this is where that choice becomes very helpful. Note that a piece of the rod dl lies completely along the x-axis and has a length dx; in fact, dl = dx in this situation. We can therefore write dm = \(\lambda\)(dx), giving us an integration variable that we know how to deal with. The distance of each piece of mass dm from the axis is given by the variable x, as shown in the figure. Putting this all together, we obtain
\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]
The last step is to be careful about our limits of integration. The rod extends from x = \(− \frac{L}{2}\) to x = \(\frac{L}{2}\), since the axis is in the middle of the rod at x = 0. This gives us
\[\begin{split} I & = \int_{- \frac{L}{2}}^{\frac{L}{2}} x^{2} \lambda dx = \lambda \frac{x^{3}}{3} \Bigg|_{- \frac{L}{2}}^{\frac{L}{2}} \\ & = \lambda \left(\dfrac{1}{3}\right) \Bigg[ \left(\dfrac{L}{2}\right)^{3} - \left(- \dfrac{L}{2}\right)^{3} \Bigg] = \lambda \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) \left(\dfrac{L^{3}}{8}\right) (2) \\ & = \frac{1}{12} ML^{2} \ldotp \end{split}\]
Next, we calculate the moment of inertia for the same uniform thin rod but with a different axis choice so we can compare the results. We would expect the moment of inertia to be smaller about an axis through the center of mass than the endpoint axis, just as it was for the barbell example at the start of this section. This happens because more mass is distributed farther from the axis of rotation.
A Uniform Thin Rod with Axis at the End
Now consider the same uniform thin rod of mass \(M\) and length \(L\), but this time we move the axis of rotation to the end of the rod. We wish to find the moment of inertia about this new axis (Figure \(\PageIndex{4}\)).
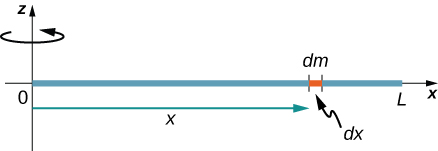
The quantity \(dm\) is again defined to be a small element of mass making up the rod. Just as before, we obtain
\[I = \int r^{2} dm = \int x^{2} dm = \int x^{2} \lambda dx \ldotp\]
However, this time we have different limits of integration. The rod extends from \(x = 0\) to \(x = L\), since the axis is at the end of the rod at \(x = 0\). Therefore we find
\[\begin{align} I & = \int_{0}^{L} x^{2} \lambda\, dx \\[4pt] &= \lambda \frac{x^{3}}{3} \Bigg|_{0}^{L} \\[4pt] &=\lambda \left(\dfrac{1}{3}\right) \Big[(L)^{3} - (0)^{3} \Big] \\[4pt] & = \lambda \left(\dfrac{1}{3}\right) L^{3} = \left(\dfrac{M}{L}\right) \left(\dfrac{1}{3}\right) L^{3} \\[4pt] &= \frac{1}{3} ML^{2} \ldotp \label{ThinRod} \end{align} \]
Note the rotational inertia of the rod about its endpoint is larger than the rotational inertia about its center (consistent with the barbell example) by a factor of four.
A Uniform Thin Disk about an Axis through the Center
Integrating to find the moment of inertia of a two-dimensional object is a little bit trickier, but one shape is commonly done at this level of study—a uniform thin disk about an axis through its center (Figure \(\PageIndex{5}\)).
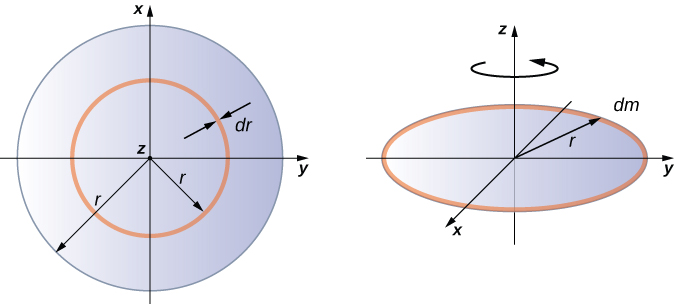
Since the disk is thin, we can take the mass as distributed entirely in the xy-plane. We again start with the relationship for the surface mass density, which is the mass per unit surface area. Since it is uniform, the surface mass density \(\sigma\) is constant:
\[\sigma = \frac{m}{A}\] or \[\sigma A = m\] so \[dm = \sigma (dA)\]
Now we use a simplification for the area. The area can be thought of as made up of a series of thin rings, where each ring is a mass increment dm of radius \(r\) equidistant from the axis, as shown in part (b) of the figure. The infinitesimal area of each ring \(dA\) is therefore given by the length of each ring (\(2 \pi r\)) times the infinitesimmal width of each ring \(dr\):
\[A = \pi r^{2},\; dA = d(\pi r^{2}) = \pi dr^{2} = 2 \pi rdr \ldotp\]
The full area of the disk is then made up from adding all the thin rings with a radius range from \(0\) to \(R\). This radius range then becomes our limits of integration for \(dr\), that is, we integrate from \(r = 0\) to \(r = R\). Putting this all together, we have
\[\begin{split} I & = \int_{0}^{R} r^{2} \sigma (2 \pi r) dr = 2 \pi \sigma \int_{0}^{R} r^{3} dr = 2 \pi \sigma \frac{r^{4}}{4} \Big|_{0}^{R} \\ & = 2 \pi \sigma \left(\dfrac{R^{4}}{4} - 0 \right) = 2 \pi \left(\dfrac{m}{A}\right) \left(\dfrac{R^{4}}{4}\right) = 2 \pi \left(\dfrac{m}{\pi R^{2}}\right) \left(\dfrac{R^{4}}{4}\right) = \frac{1}{2} mR^{2} \ldotp \end{split}\]
The Parallel-Axis Theorem
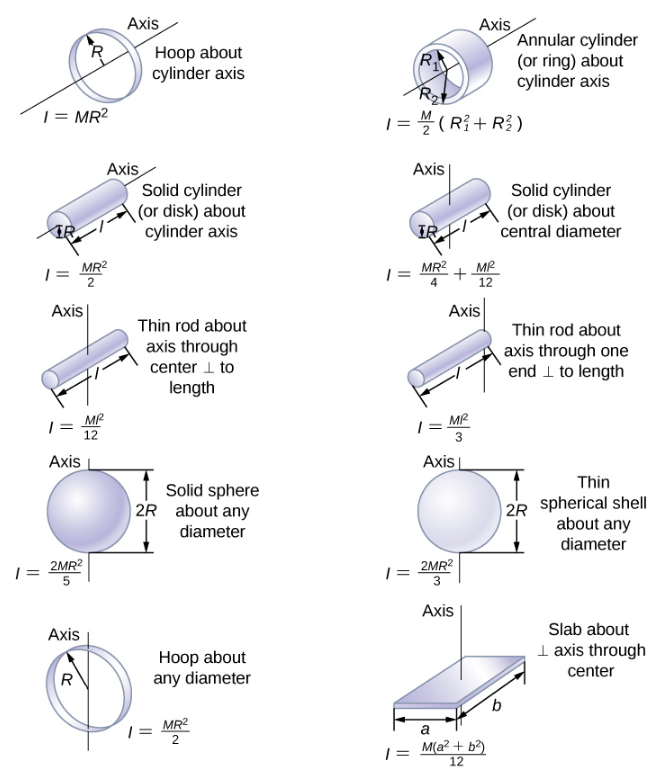
In the next section, we generalize the summation equation for point particles and develop a method to calculate moments of inertia for rigid bodies. For now, though, Figure \(\PageIndex{4}\) gives values of rotational inertia for common object shapes around specified axes.
Examples
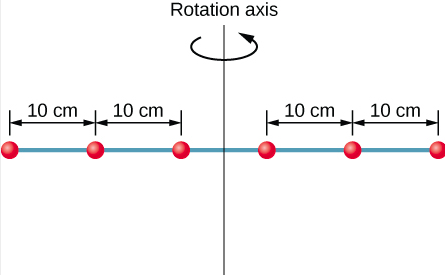
Six small washers are spaced 10 cm apart on a rod of negligible mass and 0.5 m in length. The mass of each washer is 20 g. The rod rotates about an axis located at 25 cm, as shown in Figure \(\PageIndex{3}\). (a) What is the moment of inertia of the system? (b) If the two washers closest to the axis are removed, what is the moment of inertia of the remaining four washers?
- Strategy
-
- We use the definition for moment of inertia for a system of particles and perform the summation to evaluate this quantity. The masses are all the same so we can pull that quantity in front of the summation symbol.
- We do a similar calculation.
- Solution
-
- \(I=\sum m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}+2 \times(0.05 \: \mathrm{m})^{2}\right)=0.0035 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- \(I=\sum_{j} m_{j} r_{j}^{2}=(0.02 \: \mathrm{kg})\left(2 \times(0.25 \: \mathrm{m})^{2}+2 \times(0.15 \: \mathrm{m})^{2}\right)=0.0034 \: \mathrm{kg} \cdot \mathrm{m}^{2}\)
- Significance
-
We can see the individual contributions to the moment of inertia. The masses close to the axis of rotation have a very small contribution. When we removed them, it had a very small effect on the moment of inertia.


