7.8: Calculating the Moment of Inertia For Compound Objects

Learning Objectives

• Apply the parallel axis theorem to find the moment of inertia about any axis parallel to one already known
• Calculate the moment of inertia for compound objects

In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In this subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object. This section is very useful for seeing how to apply a general equation to complex objects (a skill that is critical for more advanced physics and engineering courses).

The Parallel-Axis Theorem

The similarity between the process of finding the moment of inertia of a rod about an axis through its middle and about an axis through its end is striking, and suggests that there might be a simpler method for determining the moment of inertia for a rod about any axis parallel to the axis through the center of mass. Such an axis is called a parallel axis. There is a theorem for this, called the parallel-axis theorem, which we state here but do not derive in this text.

Theorem: Parallel axis theorem

If the moment of inertia of a rigid body about an axis through its center of mass is given by \(I_cm\), then the moment of inertia around an axis parallel to the original axis and separated from it by a distance d is given by

\[I=I_{\mathrm{cm}}+m d^{2} \ldotp \label{10.20}\]

where m is the object’s mass.

Proof

Choose coordinates such that the center of mass is at the origin, and the original axis coincides with the \(\hat{z}\) axis. Denote the position of the point in the \(xy\) plane through which the new axis \(\hat{z}'\), passes by \(d\).

 

and the distance from that point for any other point in space by \( r_d\), such that \( r =  d +  r_d\). Now calculate the moment of inertia about the new axis through \(d\):

\[\begin{align} I &=\int_{V}\left(\boldsymbol{r}_{d} \cdot \boldsymbol{r}_{d}\right) \rho \mathrm{d} V \\ &=\int_{V}(\mathbf{r} \cdot \mathbf{r}+\mathbf{d} \cdot \mathbf{d}-2 \mathbf{d} \cdot \mathbf{r}) \rho \mathrm{d} V \\ &=I_{\mathrm{cm}}+m d^{2}-2 \mathbf{d} \cdot \int_{V} \mathbf{r} \rho \mathrm{d} V \label{proof} \end{align} \]

Here \(d^2 = \boldsymbol{d}·\boldsymbol{d}\). The last integral in the last line of \ref{proof} is equal to the position of the center of mass, which we chose to be at the origin, so the last term vanishes, and we arrive at \ref{10.20}. Note that the moments of inertia of a stick satisfy the perpendicular-axis theorem.

Theorem 5.2: Perpendicular axis theorem

If a rigid object lies entirely in a plane, and the moments of inertia around two perpendicular axes x and y in that plane are \(I_x\) and \(I_y\), respectively, then the moment of inertia around the axis z perpendicular to the plane and passing through the intersection point, is given by

\[I_{z}=I_{x}+I_{y}\]

Proof

We simply calculate the moment of inertia around the z-axis (where A is the area of the object, and \(\sigma\) the mass per unit area):

\[I_{z}=\int_{A}\left(x^{2}+y^{2}\right) \sigma \mathrm{d} A=\int_{A} x^{2} \sigma \mathrm{d} A+\int_{A} y^{2} \sigma \mathrm{d} A=I_{y}+I_{x}\]

Note that the last two lines of Table 5.1 (moments of inertia of a thin planar rectangle) satisfy the parallel axis theorem.

Let’s apply this to the uniform thin rod with axis example solved in the previous section:

\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = \frac{1}{12} mL^{2} + m \left(\dfrac{L}{2}\right)^{2} = \left(\dfrac{1}{12} + \dfrac{1}{4}\right) mL^{2} = \frac{1}{3} mL^{2} \ldotp\]

This result agrees with our more lengthy calculation (Equation \ref{ThinRod}). Equation \ref{10.20} is a useful equation that we apply in some of the examples and problems.

Exrecise \(\PageIndex{1}\)

What is the moment of inertia of a cylinder of radius \(R\) and mass \(m\) about an axis through a point on the surface, as shown below?

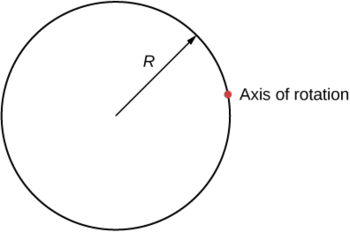
Answer

\[I_{parallel-axis} = I_{center\; of\; mass} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]

 

Calculating the Moment of Inertia for Compound Objects

Now consider a compound object such as that in Figure \(\PageIndex{6}\), which depicts a thin disk at the end of a thin rod. This cannot be easily integrated to find the moment of inertia because it is not a uniformly shaped object. However, if we go back to the initial definition of moment of inertia as a summation, we can reason that a compound object’s moment of inertia can be found from the sum of each part of the object:

\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]

It is important to note that the moments of inertia of the objects in Equation \(\PageIndex{6}\) are about a common axis. In the case of this object, that would be a rod of length L rotating about its end, and a thin disk of radius \(R\) rotating about an axis shifted off of the center by a distance \(L + R\), where \(R\) is the radius of the disk. Let’s define the mass of the rod to be m_r and the mass of the disk to be \(m_d\).

Figure \(\PageIndex{6}\): Compound object consisting of a disk at the end of a rod. The axis of rotation is located at \(A\).

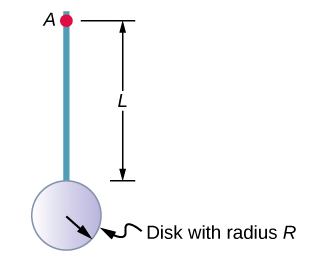
The moment of inertia of the rod is simply \(\frac{1}{3} m_rL^2\), but we have to use the parallel-axis theorem to find the moment of inertia of the disk about the axis shown. The moment of inertia of the disk about its center is \(\frac{1}{2} m_dR^2\) and we apply the parallel-axis theorem (Equation \ref{10.20}) to find

\[I_{parallel-axis} = \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]

Adding the moment of inertia of the rod plus the moment of inertia of the disk with a shifted axis of rotation, we find the moment of inertia for the compound object to be

\[I_{total} = \frac{1}{3} m_{r} L^{2} + \frac{1}{2} m_{d} R^{2} + m_{d} (L + R)^{2} \ldotp\]

Applying moment of inertia calculations to solve problems

Now let’s examine some practical applications of moment of inertia calculations.

Example \(\PageIndex{1}\): Person on a Merry-Go-Round

A 25-kg child stands at a distance \(r = 1.0\, m\) from the axis of a rotating merry-go-round (Figure \(\PageIndex{7}\)). The merry-go-round can be approximated as a uniform solid disk with a mass of 500 kg and a radius of 2.0 m. Find the moment of inertia of this system.

Figure \(\PageIndex{7}\): Calculating the moment of inertia for a child on a merry-go-round.

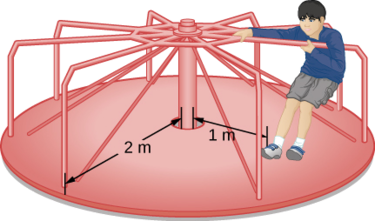
Strategy

This problem involves the calculation of a moment of inertia. We are given the mass and distance to the axis of rotation of the child as well as the mass and radius of the merry-go-round. Since the mass and size of the child are much smaller than the merry-go-round, we can approximate the child as a point mass. The notation we use is m_c = 25 kg, r_c = 1.0 m, m_m = 500 kg, r_m = 2.0 m. Our goal is to find \(I_{total} = \sum_{i} I_{i}\) (Equation \ref{10.21}).

Solution

For the child, \(I_c = m_cr^2\), and for the merry-go-round, \(I_m = \frac{1}{2}m_m r^2\). Therefore

\[I_{total} = 25(1)^{2} + \frac{1}{2} (500)(2)^{2} = 25 + 1000 = 1025\; kg\; \cdotp m^{2} \ldotp \nonumber \]

Significance

The value should be close to the moment of inertia of the merry-go-round by itself because it has much more mass distributed away from the axis than the child does.

Example \(\PageIndex{2}\): Rod and Solid Sphere

Find the moment of inertia of the rod and solid sphere combination about the two axes as shown below. The rod has length 0.5 m and mass 2.0 kg. The radius of the sphere is 20.0 cm and has mass 1.0 kg.

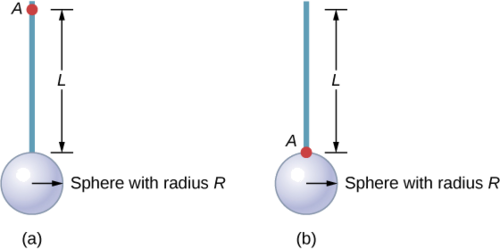
Strategy

Since we have a compound object in both cases, we can use the parallel-axis theorem to find the moment of inertia about each axis. In (a), the center of mass of the sphere is located at a distance \(L + R\) from the axis of rotation. In (b), the center of mass of the sphere is located a distance \(R\) from the axis of rotation. In both cases, the moment of inertia of the rod is about an axis at one end. Refer to Table of moments of inertia for the moments of inertia of the individual objects.

a.

\[\begin{split} I_{total} & = \sum_{i} I_{i} = I_{Rod} + I_{Sphere}; \\ I_{Sphere} & = I_{center\; of\; mass} + m_{Sphere} (L + R)^{2} = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} (L + R)^{2}; \\ I_{total} & = \frac{1}{3} (20\; kg)(0.5\; m)^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.5\; m + 0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.490)\; kg\; \cdotp m^{2} = 0.673\; kg\; \cdotp m^{2} \ldotp \end{split}\]

b.

\[\begin{split} I_{Sphere} & = \frac{2}{5} m_{Sphere} R^{2} + m_{Sphere} R^{2}; \\ I_{total} & = I_{Rod} + I_{Sphere} = \frac{1}{3} m_{Rod} L^{2} + \frac{2}{5} (1.0\; kg)(0.2\; m)^{2} + (1.0\; kg)(0.2\; m)^{2}; \\ I_{total} & = (0.167 + 0.016 + 0.04)\; kg\; \cdotp m^{2} = 0.223\; kg\; \cdotp m^{2} \ldotp \end{split}\]

Significance

Using the parallel-axis theorem eases the computation of the moment of inertia of compound objects. We see that the moment of inertia is greater in (a) than (b). This is because the axis of rotation is closer to the center of mass of the system in (b). The simple analogy is that of a rod. The moment of inertia about one end is \(\frac{1}{3}\)mL², but the moment of inertia through the center of mass along its length is \(\frac{1}{12}\)mL².