5.3: Examples
- Page ID
- 85783
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
For each of the following sets of objects, define two systems each; one that is isolated and one that is not.
- The Earth, Sun, and Moon.
- A football flying through the air, during the time after it is thrown and before it is caught. (you may ignore air resistance here)
- Two colliding carts, ignoring friction and air resistance.
- Two colliding carts, ignore air resistance but including the friction between the ground and the carts.
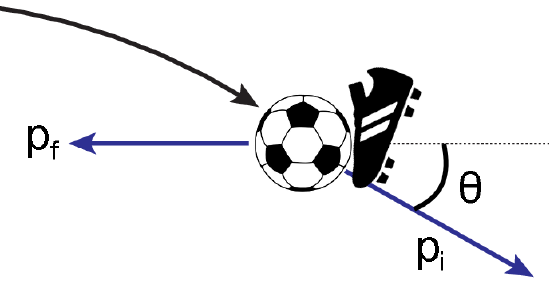A soccer player receives a pass in the air from a teammate and immediately fires the ball along the ground into the goal. The initial speed of the soccer ball is 15.0 m/s at an angle of 40.0\(^\circ\) below the horizontal. The mass of the ball is 435 g.
If this is David Beckham, he can get the shot moving with a speed of of 30.0 m/s, moving straight along the ground. What impulse (magnitude and direction) did his foot transfer to the soccer ball?
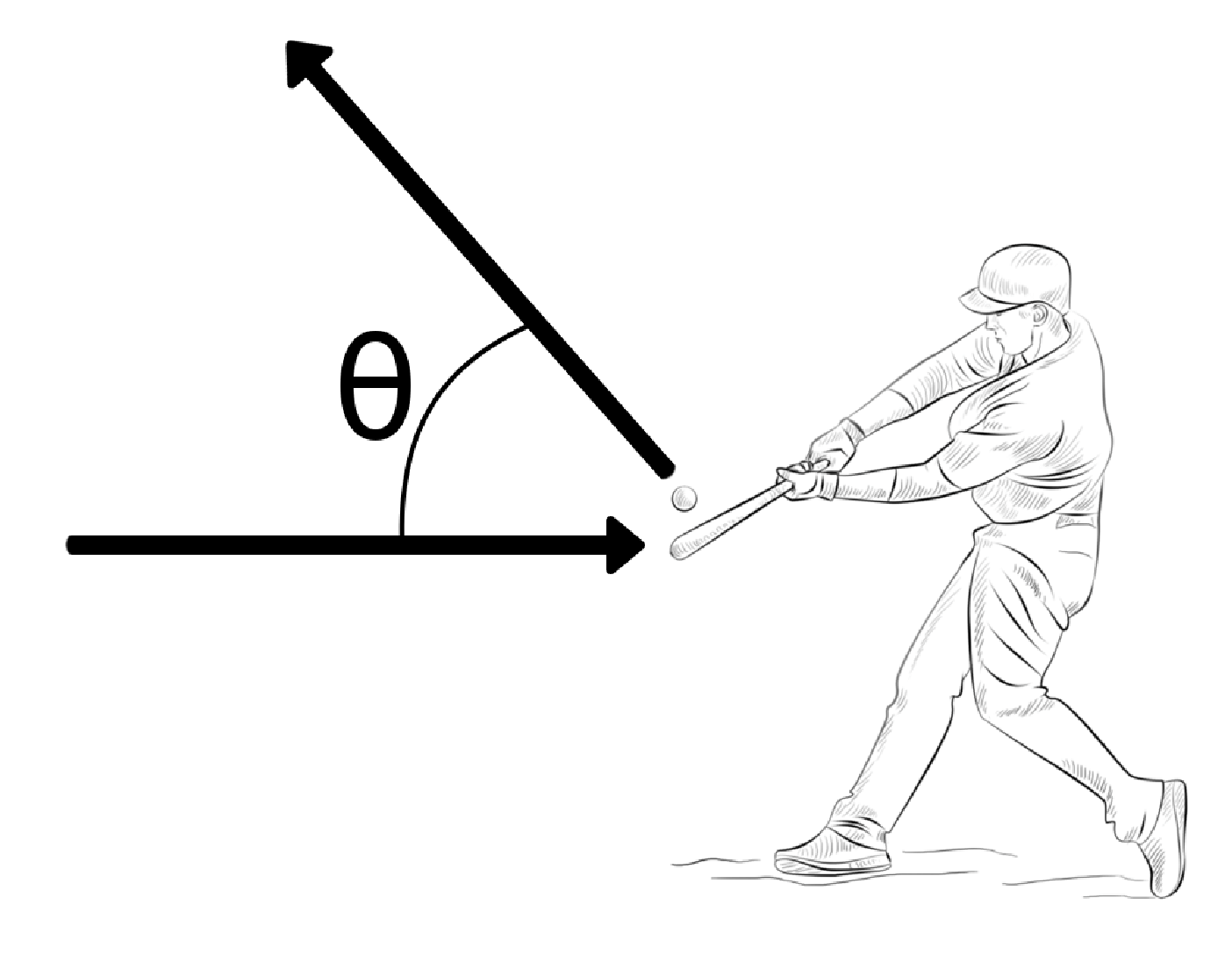A baseball player is hitting a baseball as shown in the figure. The baseball has a mass of 145 g, and is traveling at the batter at a speed of 35 m/s (that's an 80-mph fastball). The baseball player can deliver an impulse of 5.5 kg m/s to the baseball when they hit it.
- The baseball player hits the ball at an angle of 15\(^\circ\), as shown in the figure. How much impulse does the baseball player give to the ball in the x- and y-directions?
- What is the final speed of the ball?
- How much impulse was transferred to the player (through the bat) when they hit the ball?
An 80-kg hockey player (call him player 1), moving at 3 m/s to the right, collides with a 90-kg player (player 2) who was moving at 2 m/s to the left. For a brief moment, they are stuck sliding together as they grab at each other.
- What is their joint velocity as they slide together?
- What was the velocity of their center of mass before and after the collision?
Solution
(a) First we must determine whether the hockey players are isolated. We can consider them isolated from a couple of standpoints.
First of all, they are functionally isolated. This is because if they are on ice, there is very little friction and the only external forces on the hockey players are gravity and the normal force, which lead to a net zero force. (I assume this is why we are using hockey players instead of football/soccer/rugby/etc. players.)
Secondly, they are temporarily isolated due to the collision. In the collision, the collision forces are (briefly) larger than all other forces acting on the players. This is why we can do problems of football players, etc. as long as we care careful to look only right before and right after the collision. In any case, they are isolated, so we can proceed.
Call the initial velocities \(\vec{v}_{1i}\) and \(\vec{v}_{2i}\), the joint final velocity \(\vec{v}_f\). Also, call the "right" direction +x.
Then conservation of momentum reads:
\[m_{1} \begin{bmatrix} v_{1i,x} \\ 0 \\ 0 \end{bmatrix}+m_{2} \begin{bmatrix} v_{2i,x} \\ 0 \\ 0 \end{bmatrix} = \left(m_{1}+m_{2}\right) \begin{bmatrix} v_{f,x} \\ v_{f,y} \\ v_{f,z} \end{bmatrix} \label{eq:3.12b}\]
Our \(y\) and \(z\) component equations simply tell us that those velocities are zero throughout:
\[0+0=\left(m_{1}+m_{2}\right)v_{f,y} \Rightarrow v_{f,y}=0 \textrm{ and similarly } v_{f,z}=0 \label{eq.3.12c}\]
As for our \(x\) component (the interesting one):
\[ m_{1} v_{1 i,x}+m_{2} v_{2 i,x}=\left(m_{1}+m_{2}\right) v_{f,x} \label{eq:3.13} .\]
Solving for the final velocity, we get
\[ v_{f,x}=\frac{m_{1} v_{1 i,x}+m_{2} v_{2 i,x}}{m_{1}+m_{2}} \label{eq:3.14} .\]
Substituting the values given, we get
\[ v_{f,x}=\frac{80 \times 3-90 \times 2}{170}=0.353 \: \frac{\mathrm{m}}{\mathrm{s}} \label{eq:3.15} .\]
(b) According to Equation (3.3.3), the velocity of the center of mass, \(v_{cm,x}\), is just the same as what we just calculated (Equation \ref{eq:3.14}) above). This makes sense: after the collision, if the players are moving together, their system’s center of mass has to be moving with them. Also, if the system is isolated, the center of mass velocity should be the same before and after the collision. So the answer is \(v_{cm,x}\) = \(v_{f,x}\) = 0.353 m/s.
1For a variation of this problem that studies the relative velocity of this system with respect to another frame, check out Example 3.5.2 in University Physics 1 - Classical Mechanics, by Gea-Banacloche.