2.1: Coulomb’s Law
- Last updated
- Save as PDF
- Page ID
- 16533

- Boundless
- Boundless
learning objectives
- Apply the superposition principle to determine the net response caused by two or more stimuli
The superposition principle (also known as superposition property) states that: for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually. For Coulomb’s law, the stimuli are forces. Therefore, the principle suggests that total force is a vector sum of individual forces.
Coulomb Force
The scalar form of Coulomb’s Law relates the magnitude and sign of the electrostatic force F, acting simultaneously on two point charges q1 and q2:
\[| \mathrm { F } | = \dfrac { 1 } { 4 \pi a r \epsilon _ { 0 } } \dfrac { \left| q _ { 1 } q _ { 2 } \right| } { \mathrm { r } ^ { 2 } }\]
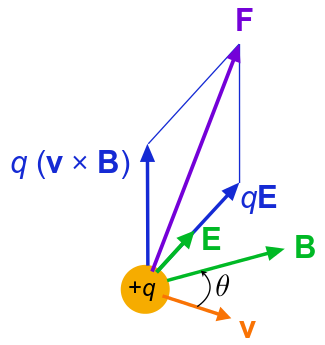
Lorentz Force on a Moving Particle: Lorentz force f on a charged particle (of charge q) in motion (instantaneous velocity v). The E field and B field vary in space and time.
where r is the separation distance and ε0 is electric permittivity. If the product q1q2 is positive, the force between them is repulsive; if q1q2 is negative, the force between them is attractive. The principle of linear superposition allows the extension of Coulomb’s law to include any number of point charges—in order to derive the force on any one point charge by a vector addition of these individual forces acting alone on that point charge. The resulting force vector happens to be parallel to the electric field vector at that point, with that point charge removed.
To calculate the force on a small test charge q at position rr, due to a system of N discrete charges:
\[\mathrm{F(r)=\dfrac{q}{4πarϵ_0} }\sum _ { i = 1 } ^ { N } q _ { i } \frac { \mathrm { r } - \mathrm { r } _ { \mathrm { i } } } { \left| \mathrm { r } - \mathrm { r } _ { \mathrm { i } } \right| ^ { 3 } } = \frac { q } { r 4 \pi a r \epsilon _ { 0 } }\sum _ { \mathrm { i } = 1 } ^ { \mathrm { N } } \mathrm { q } _ { \mathrm { i } } \dfrac { \hat { \mathrm { R } _ { i } } } { \left| \mathrm { R } _ { \mathrm { i } } \right| ^ { 2 } }\]
where qi and ri are the magnitude and position vector of the i-th charge, respectively, and \(\hat { \mathrm { R } _ { \mathrm { i } } }\) is a unit vector in the direction of \(\mathrm { R } _ { \mathrm { i } } = \mathrm { r } - \mathrm { r } _ { \mathrm { i } }\) (a vector pointing from charges qi to q. )
Of course, our discussion of superposition of forces applies to any types (or combinations) of forces. For example, when a charge is moving in the presence of a magnetic field as well as an electric field, the charge will feel both electrostatic and magnetic forces. Total force, affecting the motion of the charge, will be the vector sum of the two forces. (In this particular example of the moving charge, the force due to the presence of electromagnetic field is collectively called Lorentz force (see ).
Spherical Distribution of Charge
The charge distribution around a molecule is spherical in nature, and creates a sort of electrostatic “cloud” around the molecule.
learning objectives
- Describe shape of a Coulomb force from a spherical distribution of charge
Through the work of scientists in the late 18th century, the main features of the electrostatic force —the existence of two types of charge, the observation that like charges repel, unlike charges attract, and the decrease of force with distance—were eventually refined, and expressed as a mathematical formula. The mathematical formula for the electrostatic force is called Coulomb ‘s law after the French physicist Charles Coulomb (1736–1806), who performed experiments and first proposed a formula to calculate it.

Charge distribution in a water molecule: Schematic representation of the outer electron cloud of a neutral water molecule. The electrons spend more time near the oxygen than the hydrogens, giving a permanent charge separation as shown. Water is thus a polar molecule. It is more easily affected by electrostatic forces than molecules with uniform charge distributions.
Modern experiments have verified Coulomb’s law to great precision. For example, it has been shown that the force is inversely proportional to distance between two objects squared (F∝1/r2) to an accuracy of 1 part in 1016. No exceptions have ever been found, even at the small distances within the atom.
Coulomb’s law holds even within the atoms, correctly describing the force between the positively charged nucleus and each of the negatively charged electrons. This simple law also correctly accounts for the forces that bind atoms together to form molecules and for the forces that bind atoms and molecules together to form solids and liquids.
Generally, as the distance between ions increases, the energy of attraction approaches zero and ionic bonding is less favorable. As the magnitude of opposing charges increases, energy increases and ionic bonding is more favorable.
An electric field is a vector field which associates to each point of the space the Coulomb force that will experience a test unity charge. Given the electric field, the strength and direction of a force F on a quantity charge q in an electric field E is determined by the electric field. For a positive charge, the direction of the electric field points along lines directed radially away from the location of the point charge, while the direction is towards for a negative charge.
This distribution around a charged molecule is spherical in nature, and creates a sort of electrostatic “cloud” around the molecule. The attraction or repulsion forces within the spherical distribution of charge is stronger closer to the molecule, and becomes weaker as the distance from the molecule increases.
This image shows the outer electron cloud of a neutral water molecule. The charge distribution of the oxygen molecule is negative, and attracts the two positive hydrogen molecules. The attraction between the two opposing charges forms a neutral water molecule. It is a polar molecule because there is still a permanent charge separation because the electrons spend more time near the oxygen than the hydrogens.
Solving Problems with Vectors and Coulomb’s Law
Coulomb’s Law, which calculates the electric force between charged particles, can be written in vector notation as \(\mathrm { F } ( \mathrm { E } ) = \frac { \mathrm { kq } _ { 1 } \mathrm { q } _ { 2 } } { \mathrm { r } ^ { 2 } } \mathrm { r } +\).
learning objectives
- Explain when the vector notation of Coulomb’s Law can be used
Solving Problems with Vectors and Coulomb’s Law
Electric Force Between Two Point Charges
To address the electrostatic forces among electrically charged particles, first consider two particles with electric charges q and Q, separated in empty space by a distance r. Suppose that we want to find the electric force vector on charge q. (The electric force vector has both a magnitude and a direction. ) We can express the location of charge q as rq, and the location of charge Q as rQ. In this way we can know both how strong the electric force is on a charge, but also what direction that force is directed in. Coulomb’s Law using vectors can be written as:
\[\mathbf { F } _ { \mathbf { E } } = \dfrac { \operatorname { kq } Q \left( \mathrm { r } _ { \mathrm { q } } - \mathrm { r } _ { Q } \right) } { \left| \mathrm { r } _ { \mathrm { q } } - \mathrm { r } _ { Q } \right| ^ { 3 } }\]
In this equation, k is equal to \(\frac { 1 } { 4 \pi \varepsilon _ { 0 } \varepsilon }\) ,where \(\varepsilon _ { 0 }\) is the permittivity of free space and εε is the relative permittivity of the material in which the charges are immersed. The variables \(\mathbf { F} _ { \mathbf { E } } , \mathbf { \Gamma } _ { \mathrm { q } }\) and \(\mathbf{ R}_Q\) are in bold because they are vectors. Thus, we need to find \(\mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { Q } }\) by performing standard vector subtraction. This means that we need to subtract the corresponding components of vector\(\mathbf{r}_\mathrm{Q}}\) from vector \(\mathrmbf{r}_\mathrm{q}\).
This vector notation can be used in the simple example of two point charges where only one of which is a source of charge.
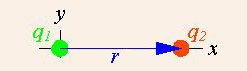
Application of Coulomb’s Law: In a simple example, the vector notation of Coulomb’s Law can be used when there are two point charges and only one of which is a source charge.
Electric Force on a Field Charge Due to Fixed Source Charges
Suppose there is more than one point source charges providing forces on a field charge. diagrams a fairly simple example with three source charges (shown in green and indexed by subscripts) and one field charge (in red, designated q). We assume that the source charges are fixed in space, and the field charge q is subject to forces from the source charges.
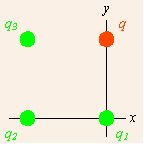
Multiple point charges: Coulomb’s Law applied to more than one point source charges providing forces on a field charge.
Note the coordinate system that has been chosen. All of the charges lie on the corners of a square, and the origin is chosen to collocate with the lower right source charge, and aligned with the square. Since we can have only one origin of coordinates, no more than one of the source points can lie at the origin, and the displacements from different source points to the field point differ. The total force on the field charge q is due to applications of the force described in the vector notation of Coulomb’s Law from each of the source charges. The total force is therefore the sum of these individual forces.
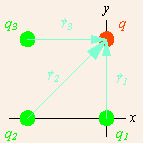
Displacements of field charge: The displacements of the field charge from each source charge are shown as light blue arrows.
Applying Coulomb’s Law three times and summing the results gives us:
\[\mathbf { F } _ { \mathbf { E } _ { \mathbf { q } } } =\dfrac { \operatorname { kq } \cdot q _ { 1 } \left( \mathbf { r } _ { q } - \mathbf { r } _ { q 1 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 1 } \right| ^ { 3 } }+ \dfrac { \mathrm { kq } \cdot \mathbf { q } _ { 2 } \left( \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 2 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 2 } \right| ^ { 3 } }+ \dfrac { \mathrm { kq } \cdot \mathrm { q } _ { 3 } \left( \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 3 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 3 } \right| ^ { 3 } }\]
This equation can further be simplified and applied to a fixed number of charge points.
\[\mathbf { F } _ { \mathbf { n } } =\sum _ { i \neq n }\dfrac { q _ { n } q _ { i } \left( \mathbf { r } _ { n } - \mathbf { r } _ { i } \right) } { 4 \pi \epsilon _ { 0 } \left| \mathbf { r } _ { \mathrm { n } } - \mathbf { r } _ { \mathrm { i } } \right| ^ { 3 } }\]
Coulomb’s Law: In this video I continue with my series of tutorial videos on Electrostatics. It’s pitched at undergraduate level and while it is mainly aimed at physics majors, it should be useful to anybody taking a first course in electricity and magnetism such as engineers etc.
Key Points
- The superposition principle suggests that the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually.
- Total Coulomb force on a test charge due to a group of charges is equal to the vector sum of all the Coulomb forces between the test charge and other individual charges.
- The superposition of forces is not limited to Coulomb forces. It applies to any types (or combinations) of forces.
- The force between two objects is inversely proportional to the square of the distance between two objects.
- The attraction or repulsion forces within the spherical distribution of charge is stronger closer to the molecule and becomes weaker as the distance from the molecule increases.
- This law also accounts for the forces that bind atoms together to form molecules and for the forces that bind atoms and molecules together to form solids and liquids.
- The vector notation of Coulomb ‘s Law can be used in the simple example of two point charges where only one of which is a source of charge.
- The total force on the field charge for multiple point source charges is the sum of these individual forces.
- Coulomb’s Law can be further simplified and applied to a fixed number of charge points.
Key Items
- Lorentz force: The force exerted on a charged particle in an electromagnetic field.
- unit vector: A vector with length 1.
- electrostatic force: The electrostatic interaction between electrically charged particles; the amount and direction of attraction or repulsion between two charged bodies.
- coulomb’s law: the mathematical equation calculating the electrostatic force vector between two charged particles
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Coulomb's law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Coulomb's_law. License: CC BY-SA: Attribution-ShareAlike
- electrostatic force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/electrostatic%20force. License: CC BY-SA: Attribution-ShareAlike
- Lorentz force. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/Lorentz_force. License: CC BY-SA: Attribution-ShareAlike
- unit vector. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/unit_vector. License: CC BY-SA: Attribution-ShareAlike
- Lorentz force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Lorentz_force. License: CC BY: Attribution
- OpenStax College, Coulombu2019s Law. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42308/latest/. License: CC BY: Attribution
- Coulomb's law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Coulomb's_law. License: CC BY-SA: Attribution-ShareAlike
- electrostatic force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/electrostatic%20force. License: CC BY-SA: Attribution-ShareAlike
- Lorentz force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Lorentz_force. License: CC BY: Attribution
- OpenStax College, Coulombu2019s Law. October 25, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42308/latest/. License: CC BY: Attribution
- George Brown, Coulomb Law Forces. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12742/latest/. License: CC BY: Attribution
- George Brown, CLF Multiple Point Sources. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12747/latest/. License: CC BY: Attribution
- Coulomb's law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Coulomb's_law. License: CC BY-SA: Attribution-ShareAlike
- electrostatic force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/electrostatic%20force. License: CC BY-SA: Attribution-ShareAlike
- Lorentz force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Lorentz_force. License: CC BY: Attribution
- OpenStax College, Coulombu2019s Law. October 25, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42308/latest/. License: CC BY: Attribution
- George Brown, CLF Multiple Point Sources. October 25, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12747/latest/. License: CC BY: Attribution
- George Brown, Coulomb Law Forces. October 25, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12742/latest/. License: CC BY: Attribution
- George Brown, CLF Multiple Point Sources. October 26, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m12747/latest/. License: CC BY: Attribution
- Coulomb's Law. Located at: http://www.youtube.com/watch?v=Fbyew6sBiOA. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license

