7.21: Potential Energy and Conservation of Energy
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 17948

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conservative and Nonconservative Forces
Conservative force—a force with the property that the work done in moving a particle between two points is independent of the path it takes.
learning objectives
- Describe properties of conservative and nonconservative forces
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done (the sum of the force acting along the path multiplied by the distance travelled) by a conservative force is zero.
A conservative force is dependent only on the position of the object. If a force is conservative, it is possible to assign a numerical value for the potential at any point. When an object moves from one location to another, the force changes the potential energy of the object by an amount that does not depend on the path taken. Gravity and spring forces are examples of conservative forces.
If a force is not conservative, then defining a scalar potential is not possible, because taking different paths would lead to conflicting potential differences between the start and end points. Nonconservative forces transfer energy from the object in motion (just like conservative force), but they do not transfer this energy back to the potential energy of the system to regain it during reverse motion. Instead, they transfer the energy from the system in an energy form which can not be used by the force to transfer it back to the object in motion. Friction is one such nonconservative force.
Path Independence of Conservative Force
Work done by the gravity in a closed path motion is zero. We can extend this observation to other conservative force systems as well. We imagine a closed path motion. We imagine this closed path motion be divided in two motions between points A and B as diagramed in Fig 1. Starting from point A to point B and then ending at point A via two work paths named 1 and 2 in the figure. The total work by the conservative force for the round trip is zero:
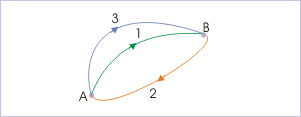
Motion Along Different Paths: Motion along different paths. For a conservative force, work done via different path is the same.
W=WAB1+WBA2=0.
Let us now change the path for motion from A to B by another path, shown as path 3. Again, the total work by the conservative force for the round trip via new route is zero: W=WAB3+WBA2=0..
Comparing two equations, WAB1=WAB3. This is true for an arbitrary path. Therefore, work done for motion from A to B by conservative force along any paths are equal.
What is Potential Energy?
Potential energy is the energy difference between the energy of an object in a given position and its energy at a reference position.
learning objectives
- Relate the potential energy and the work
Potential energy is often associated with restoring forces such as a spring or the force of gravity. The action of stretching the spring or lifting the mass of an object is performed by an external force that works against the force field of the potential. This work is stored in the force field as potential energy. If the external force is removed the force field acts on the body to perform the work as it moves the body back to its initial position, reducing the stretch of the spring or causing the body to fall. The more formal definition is that potential energy is the energy difference between the energy of an object in a given position and its energy at a reference position.

Potential Energy in a Bow and Arrow: In the case of a bow and arrow, the energy is converted from the potential energy in the archer’s arm to the potential energy in the bent limbs of the bow when the string is drawn back. When the string is released, the potential energy in the bow limbs is transferred back through the string to become kinetic energy in the arrow as it takes flight.
If the work for an applied force is independent of the path, then the work done by the force is evaluated at the start and end of the trajectory of the point of application. This means that there is a function U(x), called a “potential,” that can be evaluated at the two points x(t = t1) and x(t2) to obtain the work over any trajectory between these two points. It is tradition to define this function with a negative sign so that positive work is represented as a reduction in the potential:
\begin{align}\mathrm{W} & \mathrm{= \int_{C}F⋅dx= \int_{x(t_1)}^{x(t_2)}F⋅dx} \\ & \mathrm{=U(x(t_1))−U(x(t_2))=−ΔU.} \end{align}
Examples of Potential Energy
There are various types of potential energy, each associated with a particular type of force. More specifically, every conservative force gives rise to potential energy. For example, the work of an elastic force is called elastic potential energy; work done by the gravitational force is called gravitational potential energy; and work done by the Coulomb force is called electric potential energy.
Gravity
Gravitational energy is the potential energy associated with gravitational force, as work is required to move objects against gravity.
learning objectives
- Generate an equation that can be used to express the gravitational potential energy near the earth
Gravitational energy is the potential energy associated with gravitational force (a conservative force), as work is required to elevate objects against Earth’s gravity. The potential energy due to elevated positions is called gravitational potential energy, evidenced, for example, by water held in an elevated reservoir or behind a dam (as an example, shows Hoover Dam). If an object falls from one point to another point inside a gravitational field, the force of gravity will do positive work on the object, and the gravitational potential energy will decrease by the same amount.

Hoover Dam: Hoover dam uses the stored gravitational potential energy to generate electricity.
Potential Near Earth
Gravitational potential energy near the Earth can be expressed with respect to the height from the surface of the Earth. (The surface will be the zero point of the potential energy. ) We can express the potential energy (gravitational potential energy) as:
\mathrm{PE=mgh,}
where PE = potential energy measured in joules (J), m = mass of the object (measured in kg), and h = perpendicular height from the reference point (measured in m); g = gravitational acceleration (9.8m/s2). Near the surface of the Earth, g can be considered constant.
General Formula
However, over large variations in distance, the approximation that g is constant is no longer valid. Instead, we must use calculus and the general mathematical definition of work to determine gravitational potential energy. For the computation of the potential energy we can integrate the gravitational force, whose magnitude is given by Newton’s law of gravitation (with respect to the distance r between the two bodies). Using that definition, the gravitational potential energy of a system of masses m and M at a distance r using gravitational constant G is:
\mathrm{U(r) = \int_r (G \dfrac{mM}{r'^{2}} ) dr' = -G \dfrac{mM}{r} + K, }
where K is the constant of integration. Choosing the convention that K=0 makes calculations simpler, albeit at the cost of making U negative. For this choice, the potential at infinity is defined as 0.
Springs
When a spring is stretched/compressed from its equilibrium position by x, its potential energy is give as \mathrm{U=\frac{1}{2}kx^2}.
learning objectives
- Explain how potential energy is stored in springs
Spring force is conservative force, given by the Hooke’s law: \mathrm{F = -kx}, where k is spring constant, measured experimentally for a particular spring and x is the displacement. We would like to obtain an expression for the work done to the spring. From the conservation of mechanical energy (Check our Atom on “Conservation of Mechanical Energy), the work should be equal to the potential energy stored in spring. The displacement x is usually measured from the position of “neutral length” or “relaxed length” – the length of spring corresponding to situation when spring is neither stretched nor compressed. We shall identify this position as the origin of coordinate reference (x=0).
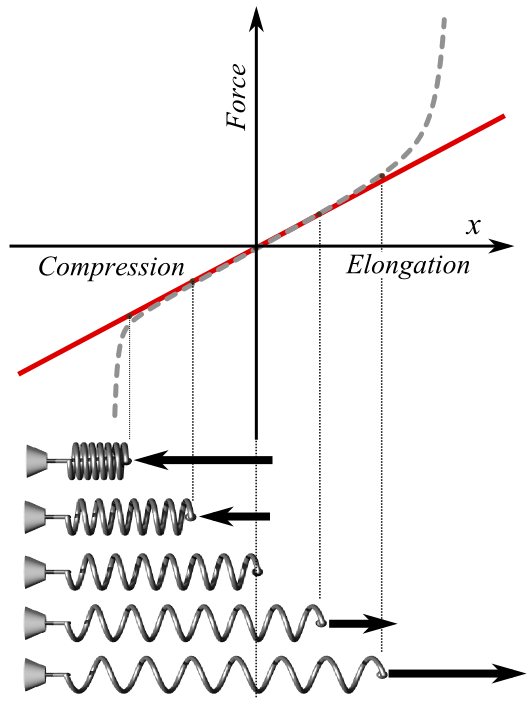
Hooke’s Law: Plot of applied force F vs. elongation X for a helical spring according to Hooke’s law (solid line) and what the actual plot might look like (dashed line). Red is used extension, blue for compression. At bottom, schematic pictures of spring states corresponding to some points of the plot; the middle one is in the relaxed state (no force applied).
Let \mathrm{x = 0} and \mathrm{x = x_f (>0)} be the initial and final positions of the block attached to the string. As the block slowly moves, we do work W on the spring: \mathrm{W=\int_{0}^{x_f}(kx)dx=\frac{1}{2}kx_f^2}. When we stretch the spring. We have to apply force in the same direction as the displacement. (Technically, work is given as the inner product of the two vectors: force and displacement. \mathrm{W=F⋅Δx}). Therefore, the overall sign in the integral is +, not -.
If the block is gently released from the stretched position (\mathrm{x = x_f}\), the stored potential energy in the spring will start to be converted to the kinetic energy of the block, and vice versa. Neglecting frictional forces, Mechanical energy conservation demands that, at any point during its motion,
\begin{align} \mathrm{Total \; Energy} & \mathrm{= \dfrac{1}{2}mv^2+\dfrac{1}{2}kx^2} \\ & \mathrm{=\dfrac{1}{2}kx_f^2=constant.} \end{align}
From the energy conservation, we can estimate that, by the time the block reaches x=0 position, its speed will be \mathrm{v(x=0)=\sqrt{\frac{k}{m}}x_f}. The block will keep oscillating between x = -xf and xf.
Conservation of Mechanical Energy
Conservation of mechanical energy states that the mechanical energy of an isolated system remains constant without friction.
learning objectives
- Formulate the principle of the conservation of the mechanical energy
Conservation of mechanical energy states that the mechanical energy of an isolated system remains constant in time, as long as the system is free of all frictional forces. In any real situation, frictional forces and other non-conservative forces are always present, but in many cases their effects on the system are so small that the principle of conservation of mechanical energy can be used as a fair approximation. An example of a such a system is shown in. Though energy cannot be created nor destroyed in an isolated system, it can be internally converted to any other form of energy.
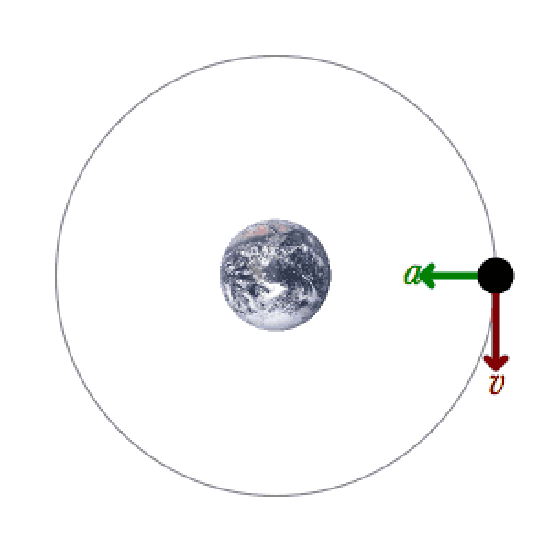
A Mechanical System: An example of a mechanical system: A satellite is orbiting the Earth only influenced by the conservative gravitational force and the mechanical energy is therefore conserved. This acceleration is represented by a green acceleration vector and the velocity is represented by a red velocity vector.
Derivation
Let us consider what form the work -energy theorem takes when only conservative forces are involved (leading us to the conservation of energy principle). The work-energy theorem states that the net work done by all forces acting on a system equals its change in kinetic energy (KE). In equation form, this is:
\mathrm{W_{net}=\dfrac{1}{2}mv^2−\dfrac{1}{2}mv_0^2=ΔKE.}
If only conservative forces act, then \mathrm{W_{net} = W_c}, where Wc is the total work done by all conservative forces. Thus, \mathrm{W_c = \Delta KE}.
Now, if the conservative force, such as the gravitational force or a spring force, does work, the system loses potential energy (PE). That is, \mathrm{W_c = -PE}. Therefore,
\mathrm{−ΔPE=ΔKE}
This equation means that the total kinetic and potential energy is constant for any process involving only conservative forces. That is,
\mathrm{KE+PE=const \; or \; KE_i+PE_i=KE_f+PE_f,}
where i and f denote initial and final values. This equation is a form of the work-energy theorem for conservative forces; it is known as the conservation of mechanical energy principle.
Remember that the law applies to the extent that all the forces are conservative, so that friction is negligible. The total kinetic plus potential energy of a system is defined to be its mechanical energy (\mathrm{KE+PE}). In a system that experiences only conservative forces, there is a potential energy associated with each force, and the energy only changes form between KE and various types of PE (with the total energy remaining constant).
Conservation of Mechanical Energy: Worked example.
Problem Solving With the Conservation of Energy
To solve a conservation of energy problem determine the system of interest, apply law of conservation of energy, and solve for the unknown.
learning objectives
- Identify steps necessary to solve a conservation of energy problem
Problem-solving Strategy
You should follow a series of steps whenever you are problem solving:
Step One
Determine the system of interest and identify what information is given and what quantity is to be calculated. For example, let’s assume you have the problem with car on a roller coaster. You know that the cars of a roller coaster reach their maximum kinetic energy (KEKE) when at the bottom of their path. When they start rising, the kinetic energy begins to be converted to gravitational potential energy (PEgPEg). The sum of kinetic and potential energy in the system should remain constant, if losses to friction are ignored.

Determining Energy: The cars of a roller coaster reach their maximum kinetic energy when at the bottom of their path. When they start rising, the kinetic energy begins to be converted to gravitational potential energy. The sum of kinetic and potential energy in the system remains constant, ignoring losses to friction.
Step Two
Examine all the forces involved and determine whether you know or are given the potential energy from the work done by the forces. Then use step three or step four.
Step Three
If you know the potential energies (\mathrm{PE}) for the forces that enter into the problem, then forces are all conservative, and you can apply conservation of mechanical energy simply in terms of potential and kinetic energy. The equation expressing conservation of energy is:
\mathrm{KE_i+PE_i=KE_f+PE_f.}
Step Four
If you know the potential energy for only some of the forces, then the conservation of energy law in its most general form must be used:
\mathrm{KE_i+PE_i+W_{nc}+OE_i=KE_f+PE_f+OE_f}
where \mathrm{O_E} stand for all other energies, and \mathrm{W_{nc}} stands for work done by non-conservative forces. In most problems, one or more of the terms is zero, simplifying its solution. Do not calculate \mathrm{W_c}, the work done by conservative forces; it is already incorporated in the \mathrm{PE} terms.
Step Five
You have already identified the types of work and energy involved (in step two). Before solving for the unknown, eliminate terms wherever possible to simplify the algebra. For example, choose height \mathrm{h=0} at either the initial or final point—this will allow to set \mathrm{PEg} at zero. Then solve for the unknown in the customary manner.
Step Six
Check the answer to see if it is reasonable. Once you have solved a problem, reexamine the forms of work and energy to see if you have set up the conservation of energy equation correctly. For example, work done against friction should be negative, potential energy at the bottom of a hill should be less than that at the top, and so on.
Energy conservation: Part of a series of videos on physics problem-solving. The problems are taken from “The Joy of Physics. ” This one deals with energy conservation. The viewer is urged to pause the video at the problem statement and work the problem before watching the rest of the video.
Problem Solving with Dissipative Forces
In the presence of dissipative forces, total mechanical energy changes by exactly the amount of work done by nonconservative forces (Wc).
learning objectives
- Express the energy conservation relationship that can be applied to solve problems with dissipative forces
INTRODUCTION
We have seen a problem-solving strategy with the conservation of energy in the previous section. Here we will adopt the strategy for problems with dissipative forces. Since the work done by nonconservative (or dissipative) forces will irreversibly alter the energy of the system, the total mechanical energy (KE + PE) changes by exactly the amount of work done by nonconservative forces (Wc). Therefore, we obtain \mathrm{KE_i+PE_i+W_{nc}=KE_f+PE_f}, where KE and PE represent kinetic and potential energies respectively. Therefore, using the new energy conservation relationship, we can apply the same problem-solving strategy as with the case of conservative forces.
EXAMPLE
Consider the situation shown in, where a baseball player slides to a stop on level ground. Using energy considerations, calculate the distance the 65.0-kg baseball player slides, given that his initial speed is 6.00 m/s and the force of friction against him is a constant 450 N.
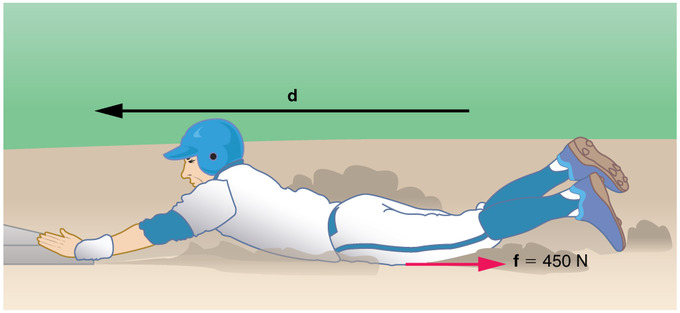
Fig 1: The baseball player slides to a stop in a distance d. In the process, friction removes the player’s kinetic energy by doing an amount of work fd equal to the initial kinetic energy.
Strategy: Friction stops the player by converting his kinetic energy into other forms, including thermal energy. In terms of the work-energy theorem, the work done by friction (f), which is negative, is added to the initial kinetic energy to reduce it to zero. The work done by friction is negative, because f is in the opposite direction of the motion (that is, \mathrm{θ=180º}, and so \mathrm{ \cos θ=−1}). Thus \mathrm{W_{nc} = -fd}. The equation simplifies to \mathrm{\frac{1}{2}mv_i^2−fd=0}.
Solution: Solving the previous equation for d and substituting known values yields, we get d = 2.60 m. The most important point of this example is that the amount of nonconservative work equals the change in mechanical energy.
Key Points
- If a particle travels in a closed loop, the net work done (the sum of the force acting along the path multiplied by the distance travelled) by a conservative force is zero.
- Conservative force is dependent only on the position of the object. If a force is conservative, it is possible to assign a numerical value for the potential at any point.
- Nonconservative force transfer the energy from the system in an energy form which can not be used by the force to transfer back to the object in motion.
- If the work for an applied force is independent of the path, then the work done by the force is evaluated at the start and end of the trajectory of the point of application. This means that there is a function U(x), called a ” potential “.
- It is tradition to define the potential function with a negative sign so that positive work is represented as a reduction in the potential.
- Every conservative force gives rise to potential energy. Examples are elastic potential energy, gravitational potential energy, and electric potential energy.
- Gravitational potential energy near the earth can be expressed with respect to the height from the surface of the Earth as PE = mgh. g = gravitational acceleration (9.8m/s2). Near the surface of the Earth, g can be considered constant.
- Over large variations in distance, the approximation that g is constant is no longer valid and a general formula should be used for the potential. It is given as: \mathrm{U(r)= \int_r (G\frac{mM}{r′^2})dr′=−G\frac{mM}{r} +K}.
- Choosing the convention that the constant of integration K=0 assumes that the potential at infinity is defined to be 0.
- The displacement of spring x is usually measured from the position of “neutral length ” or “relaxed length”. Often, it is most convenient to identify this position as the origin of coordinate reference (x=0).
- If the block is gently released from the stretched position (\mathrm{x = x_f}), energy conservation tells us that \mathrm{\frac{1}{2}mv^2+\frac{1}{2}kx^2=\frac{1}{2}kx_f^2=constant}.
- If the block is released from the stretched position (\mathrm{x = x_f}), by the time the block reaches x=0 position, its speed will be \mathrm{v(x=0)=\sqrt{\frac{k}{m}}x_f}. The block will keep oscillating between \mathrm{x = -x_f} and \mathrm{x_f}.
- The conservation of mechanical energy can be written as “\mathrm{KE + PE = const}”.
- Though energy cannot be created nor destroyed in an isolated system, it can be internally converted to any other form of energy.
- In a system that experiences only conservative forces, there is a potential energy associated with each force, and the energy only changes form between KE and various types of PE, with the total energy remaining constant.
- If you know the potential energies for the forces that enter into the problem, then forces are all conservative, and you can apply conservation of mechanical energy simply in terms of potential and kinetic energy. The equation expressing conservation of energy is: \mathrm{KE_i+PE_i=KE_f+PE_f.} .
- If you know the potential energy for only some of the forces, then the conservation of energy law in its most general form must be used: \mathrm{KE_i+PE_i+W_{nc}+OE_i=KE_f+PE_f+OE_f} , where OE stands for all other energies.
- Once you have solved a problem, always check the answer to see if it is reasonable.
- Using the new energy conservation relationship \mathrm{KE_i+PE_i+W_{nc}=KE_f+PE_f}, we can apply the same problem-solving strategy as with the case of conservative forces.
- The most important point is that the amount of nonconservative work equals the change in mechanical energy.
- The work done by nonconservative (or dissipative) forces will irreversibly dissipated in the system.
Key Terms
- potential: A curve describing the situation where the difference in the potential energies of an object in two different positions depends only on those positions.
- Coulomb force: the electrostatic force between two charges, as described by Coulomb’s law
- potential: A curve describing the situation where the difference in the potential energies of an object in two different positions depends only on those positions.
- conservative force: A force with the property that the work done in moving a particle between two points is independent of the path taken.
- Hooke’s law: the principle that the stress applied to a solid is directly proportional to the strain produced. This law describes the behavior of springs and solids stressed within their elastic limit.
- conservation: A particular measurable property of an isolated physical system does not change as the system evolves.
- isolated system: A system that does not interact with its surroundings, that is, its total energy and mass stay constant.
- frictional force: Frictional force is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other.
- kinetic energy: The energy possessed by an object because of its motion, equal to one half the mass of the body times the square of its velocity.
- potential energy: The energy an object has because of its position (in a gravitational or electric field) or its condition (as a stretched or compressed spring, as a chemical reactant, or by having rest mass)
- conservative force: A force with the property that the work done in moving a particle between two points is independent of the path taken.
- dissipative force: A force resulting in dissipation, a process in which energy (internal, bulk flow kinetic, or system potential) is transformed from some initial form to some irreversible final form.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Conservative force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Conservative_force. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Conservative Force. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14104/latest/. License: CC BY: Attribution
- curl. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/curl. License: CC BY-SA: Attribution-ShareAlike
- potential. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/potential. License: CC BY-SA: Attribution-ShareAlike
- gradient. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/gradient. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Conservative Force. February 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14104/latest/. License: CC BY: Attribution
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY-SA: Attribution-ShareAlike
- potential. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/potential. License: CC BY-SA: Attribution-ShareAlike
- Coulomb force. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/Coulomb_force. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Conservative Force. February 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14104/latest/. License: CC BY: Attribution
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY: Attribution
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY-SA: Attribution-ShareAlike
- Free High School Science Texts Project, Gravity and Mechanical Energy: Potential Energy. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m40047/latest/. License: CC BY: Attribution
- conservative force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/conservative%20force. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Conservative Force. February 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14104/latest/. License: CC BY: Attribution
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY: Attribution
- Dam. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Dam. License: CC BY: Attribution
- Sunil Kumar Singh, Work by Spring Force. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14102/latest/. License: CC BY: Attribution
- conservative force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/conservative%20force. License: CC BY-SA: Attribution-ShareAlike
- Hooke's law. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/Hooke's_law. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Conservative Force. February 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14104/latest/. License: CC BY: Attribution
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY: Attribution
- Dam. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Dam. License: CC BY: Attribution
- HookesLawForSpring-English. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:HookesLawForSpring-English.png. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Conservative Forces and Potential Energy. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42149/latest/. License: CC BY: Attribution
- Mechanical energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Mechanical_energy%23Conservation_and_interconversion_of_energy. License: CC BY-SA: Attribution-ShareAlike
- conservation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/conservation. License: CC BY-SA: Attribution-ShareAlike
- frictional force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/frictional%20force. License: CC BY-SA: Attribution-ShareAlike
- isolated system. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/isolated_system. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Conservative Force. February 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14104/latest/. License: CC BY: Attribution
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY: Attribution
- Dam. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Dam. License: CC BY: Attribution
- HookesLawForSpring-English. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:HookesLawForSpring-English.png. License: CC BY-SA: Attribution-ShareAlike
- Mechanical energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Mechanical_energy%23Conservation_and_interconversion_of_energy. License: CC BY: Attribution
- Conservation of Mechanical Energy. Located at: http://www.youtube.com/watch?v=n637fBmj9Ko. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Conservation of Energy. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42151/latest/. License: CC BY: Attribution
- Kinetic energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Kinetic_energy. License: CC BY-SA: Attribution-ShareAlike
- kinetic energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/kinetic%20energy. License: CC BY-SA: Attribution-ShareAlike
- conservative force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/conservative%20force. License: CC BY-SA: Attribution-ShareAlike
- potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/potential%20energy. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Conservative Force. February 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14104/latest/. License: CC BY: Attribution
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY: Attribution
- Dam. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Dam. License: CC BY: Attribution
- HookesLawForSpring-English. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:HookesLawForSpring-English.png. License: CC BY-SA: Attribution-ShareAlike
- Mechanical energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Mechanical_energy%23Conservation_and_interconversion_of_energy. License: CC BY: Attribution
- Conservation of Mechanical Energy. Located at: http://www.youtube.com/watch?v=n637fBmj9Ko. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Energy conservation. Located at: http://www.youtube.com/watch?v=TIzC5TBIJNM. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/3/30/Wooden_roller_coaster_txgi.jpg/486px-Wooden_roller_coaster_txgi.jpg. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Nonconservative Forces. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42150/latest/. License: CC BY: Attribution
- dissipative force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/dissipative%20force. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Conservative Force. February 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14104/latest/. License: CC BY: Attribution
- Potential energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Potential_energy. License: CC BY: Attribution
- Dam. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Dam. License: CC BY: Attribution
- HookesLawForSpring-English. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:HookesLawForSpring-English.png. License: CC BY-SA: Attribution-ShareAlike
- Mechanical energy. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Mechanical_energy%23Conservation_and_interconversion_of_energy. License: CC BY: Attribution
- Conservation of Mechanical Energy. Located at: http://www.youtube.com/watch?v=n637fBmj9Ko. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Energy conservation. Located at: http://www.youtube.com/watch?v=TIzC5TBIJNM. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/3/30/Wooden_roller_coaster_txgi.jpg/486px-Wooden_roller_coaster_txgi.jpg. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Nonconservative Forces. February 3, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42150/latest/. License: CC BY: Attribution



