9.6: Applications of Statics
- Last updated
- Save as PDF
- Page ID
- 17985

- Boundless
- Boundless
learning objectives
- Develop an understanding of how a machine applies force to work against a load force
Simple Machines
A simple machine is a device that changes the direction or magnitude of a force. They can be described as the simplest mechanisms that use mechanical advantage (or leverage) to multiply force. Usually, the term “simple machine” is referring to one of the six classical simple machines, defined by Renaissance scientists.
Simple Machines, Pulleys; Forces, Distances and MA: Describes the following terms as they relate to simple machine; input force, output force, input distance, output distance, mechanical advantage.
Simple machines are devices used to multiply or augment a force that we apply—often at the expense of a distance through which we apply the force. Some common examples include:
- Lever
- Wheel and Axle
- Pulley
- Inclined Plane
- Wedge
- Screw
When a device with a specific movement, called a mechanism, is joined with others to form a machine, these machines can be broken down into elementary movements. For example, a bicycle is a mechanism made up of wheels, levers, and pulleys.
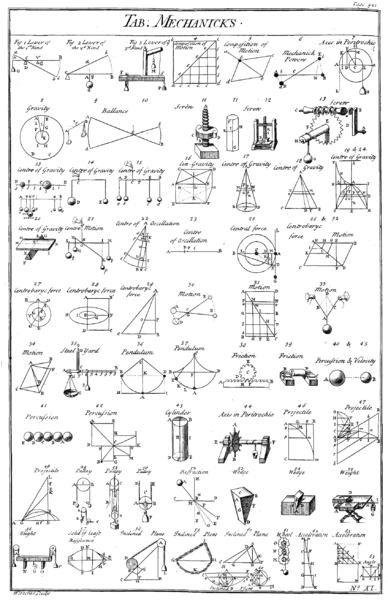
Simple Machines: Table of simple mechanisms, from Chambers’ Cyclopedia, 1728. [1] Simple machines provide a “vocabulary” for understanding more complex machines.
Mechanics
A simple machine has an applied force that works against a load force. If there are no frictional losses, the work done on the load is equal to the work done by the applied force. This allows an increase in the output force at the cost of a proportional decrease in distance moved by the load. The ratio of the output force to the input force is the mechanical advantage of the machine. If the machine does not absorb energy, its mechanical advantage can be calculated from the machine’s geometry. For instance, the mechanical advantage of a lever is equal to the ratio of its lever arms.
Simple machines which do not experience frictional losses are called ideal machines. For these ideal machines, the power in (rate of energy input) in equal to the power out (rate of energy output): Pin=PoutPin=Pout.
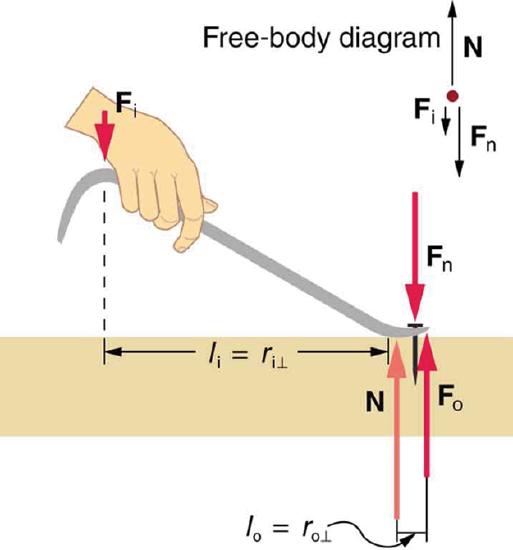
Lever: The amount of force produced by a machine can not be greater than the amount of force put into it.
Further Examples
Wheelbarrows and shovels are also examples of simple machines (these utilize levers). They use only three forces: the input force, output force, and force on the pivot. In the case of wheelbarrows, the output force is between the pivot (wheel’s axle) and the input force. In the shovel, the input force is between the pivot and the load.
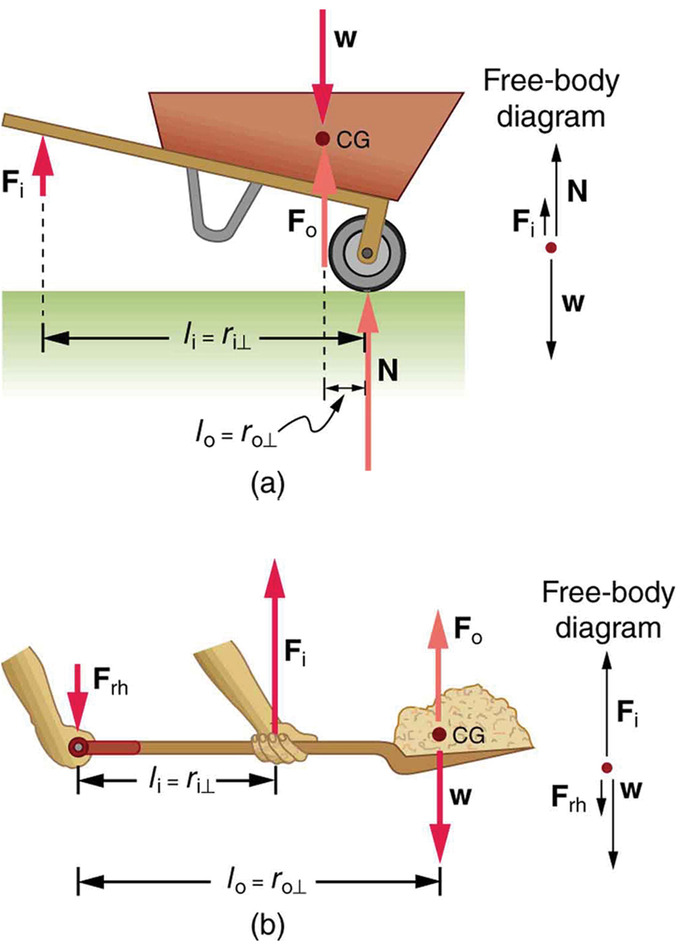
Examples of Simple Machines: Both of these machines use the concept of levers.
Arches and Domes
Arches and domes are structures that exhibit structural strength and can span large areas with no intermediate supports.
learning objectives
- Explain how an arch exhibits structural strength and how a dome can span a large area without intermediate supports
Arches and domes are structures that exhibit structural strength and can span large areas with no intermediate supports. In this atom, we will discuss the history and physics behind arches and domes.
Arches
An arch is a structure that spans a space, and supports structure and weight above it. Arches have been being built from as long ago as the second millennium, but were not used for a variety of structures until the Romans took advantage of their capabilities. Arches are a pure compression form. They span large areas by resolving forces into compressive stresses and eliminating tensile stresses (referred to as arch action). As the forces in an arch are carried toward the ground, the arch will push outward at the base (called thrust ). As the height of the arch decreases, the outward thrust increases. To prevent the arch from collapsing, the thrust needs to be restrained, either with internal ties or external bracing. This external bracing is often called an abutment, as shown in.
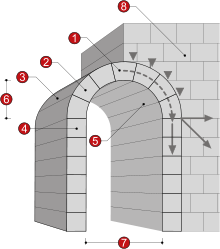
Arches: A masonry arch1. Keystone 2. Voussoir 3. Extrados 4. Impost 5. Intrados 6. Rise 7. Clear span 8. Abutment
The most common true arch configurations are the fixed arch, the two-hinged arch and the three-hinged arch. The fixed arch is most often used in reinforced concrete bridge and tunnel construction, where the spans are short. Because it is subject to additional internal stress caused by thermal expansion and contraction, this type of arch is considered to be statically indeterminate. The two-hinged arch is most often used to bridge long spans. This type of arch has pinned connections at the base. Unlike the fixed arch, the pinned base is able to rotate, allowing the structure to move freely and compensate for the thermal expansion and contraction caused by changes in outdoor temperature. Because the structure is pinned between the two base connections, which can result in additional stresses, the two-hinged arch is also statically indeterminate, although not to the degree of the fixed arch.
Domes
A dome is an element of architecture that resembles the hollow upper half of a sphere. Dome structures made of various materials (from mud to stone, wood, brick, concrete, metal, glass and plastic) and have a long architectural lineage extending into prehistory.
A dome is basically an arch that has been rotated around its central vertical axis. Domes have the same properties and capabilities of arches, they can span large areas without intermediate supports and have a great deal of structural strength. When the base of a dome is not the same shape as its supporting walls, for example when a circular dome is on a square structure, techniques are employed to transition between the two. Pendentives are triangular sections of a sphere used to transition from the flat surfaces of supporting walls to the round base of a dome.
Domes can be divided into two kinds, simple and compound. Simple domes use pendentives that are part of the same sphere as the dome itself. Compound domes are part of the structure of a large sphere below that of the dome itself, forming a circular base, as shown in.

Compound Dome: A compound dome (red) with pendentives (yellow) from a sphere of greater radius than the dome.
Muscles and Joints
Most skeletal muscles and joints exert much larger forces within the body than the limbs will apply to the outside world.
learning objectives
- Explain the forces exerted by muscles
Muscles and Joints
Muscles and joints involve very interesting applications of statics. Muscles can only contract, so they occur in pairs. In the arm, the biceps muscle is a flexor: it closes the limb. The triceps muscle is an extensor that opens the limb. This configuration is typical of skeletal muscles, bones, and joints in humans and other vertebrates. Most skeletal muscles exert much larger forces within the body than the limbs will apply to the outside world. The reason is clear, since most muscles are attached to bones via tendons close to joints, causing these systems to have mechanical advantages much less than one. Viewing them as simple machines, the input force is much greater than the output force, as seen in.
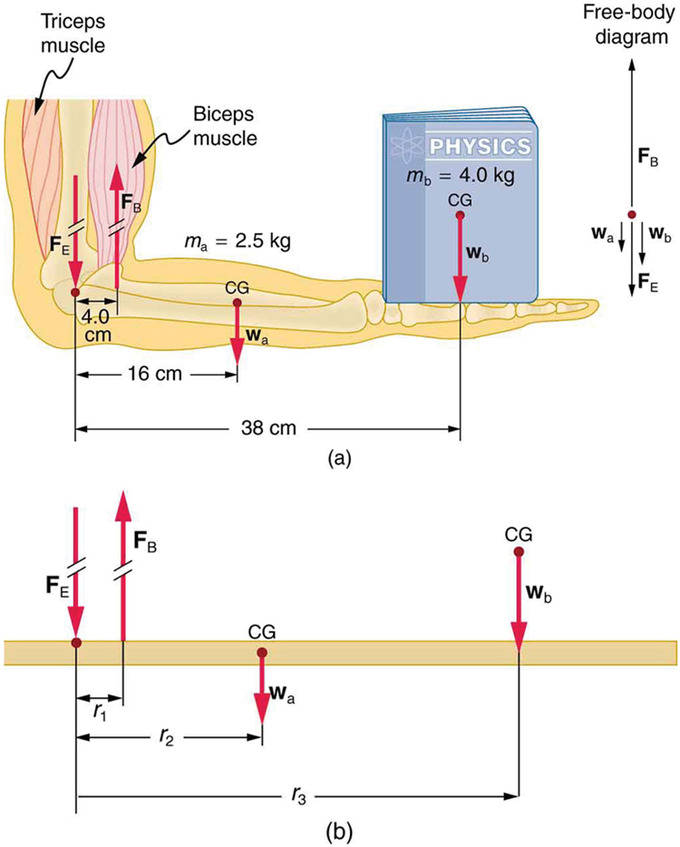
The Forearm of a Person Holding a Book: (a. ) The biceps exert a force FB to support the weight of the forearm and the book. The triceps are assumed to be relaxed. (b.) An approximately equivalent mechanical system with the pivot at the elbow joint
Very large forces are also created in the joints. Because muscles can contract but not expand beyond their resting length, joints and muscles often exert forces that act in opposite directions, and thus subtract. Forces in muscles and joints are largest when their load is far from the joint. For example, in racquet sports like tennis, the constant extension of the arm during game play creates large forces. The mass times the lever arm of a tennis racquet is an important factor, and many players use the heaviest racquet they can handle. It is no wonder that joint deterioration and damage to the tendons in the elbow, such as ‘tennis elbow,’ can result from repetitive motion, undue torques, and possible poor racquet selection in such sports.
Various tried techniques for holding and using a racquet, bat, or stick can not only increase sporting prowess but can minimize fatigue and long-term damage to the body. Training coaches and physical therapists use the knowledge of the relationships between forces and torques in the treatment of muscles and joints. In physical therapy, an exercise routine can apply a particular force and torque, which can revive muscles and joints in time. Some exercises should be performed under water, thus requiring the exertion of more force and further strengthening muscles.
Key Points
- The six classifications of simple machines were established by renaissance scientists; they are as follows: lever, wheel and axle, pulley, inclined plane, wedge and screw.
- Simple machines can be joined with other devices to create a more complicated machine. These building blocks are used to explain how machines work.
- The force output by a simple machine can exceed the force that was put into the machine.
- Arches span large areas by resolving forces into compressive stresses and eliminating tensile stresses.
- The most common true arch configurations are the fixed arch, the two-hinged arch, and the three-hinged arch.
- A dome is basically an arch that has been rotated around its central vertical axis.
- Domes are basically arches that have been rotated on their vertical axis, and have the same capabilities and properties of arches.
- Domes can be divided into two kinds, simple and compound.
- It is helpful to view muscles as a simple machines and draw them as free body diagrams.
- In muscles, the input force is often much greater than the output force.
- Very large forces are also created in the joints. Because muscles can contract but not expand beyond their resting length, joints and muscles often exert forces that act in opposite directions, and thus subtract.
Key Terms
- machine: A mechanical or electrical device that performs or assists in the performance of human tasks, whether physical or computational, laborious or for entertainment.
- leverage: A force amplified by means of a lever rotating around a pivot.
- mechanical advantage: In a simple machine, the ratio of the output force to the input force.
- compressive stress: Stress on materials that leads to a smaller volume.
- tensile stress: Stress state leading to expansion; that is, the length of a material tends to increase in the tensile direction while the volume remains constant.
- pendentive: The concave triangular sections of vaulting that provide the transition between a dome and the square base on which it is set and transfer the weight of the dome.
- muscle: A contractile form of tissue which animals use to effect movement.
- joint: Any part of the body where two bones join, in most cases allowing that part of the body to be bent or straightened.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, Simple Machines. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42174/latest/. License: CC BY: Attribution
- Simple machines. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Simple_machines. License: CC BY-SA: Attribution-ShareAlike
- leverage. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/leverage. License: CC BY-SA: Attribution-ShareAlike
- machine. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/machine. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Simple Machines. February 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42174/latest/. License: CC BY: Attribution
- Table of Mechanicks, Cyclopaedia, Volume 2. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Table_of_Mechanicks,_Cyclopaedia,_Volume_2.png. License: Public Domain: No Known Copyright
- OpenStax College, Simple Machines. February 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42174/latest/. License: CC BY: Attribution
- Simple Machines, Pulleys; Forces, Distances and MA. Located at: http://www.youtube.com/watch?v=BJ9MELhhW6U. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Arch. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Arch. License: CC BY-SA: Attribution-ShareAlike
- Dome. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Dome%23General_types. License: CC BY-SA: Attribution-ShareAlike
- pendentive. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/pendentive. License: CC BY-SA: Attribution-ShareAlike
- compressive stress. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/compressive%20stress. License: CC BY-SA: Attribution-ShareAlike
- tensile stress. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/tensile%20stress. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Simple Machines. February 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42174/latest/. License: CC BY: Attribution
- Table of Mechanicks, Cyclopaedia, Volume 2. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Table_of_Mechanicks,_Cyclopaedia,_Volume_2.png. License: Public Domain: No Known Copyright
- OpenStax College, Simple Machines. February 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42174/latest/. License: CC BY: Attribution
- Simple Machines, Pulleys; Forces, Distances and MA. Located at: http://www.youtube.com/watch?v=BJ9MELhhW6U. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Arch. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Arch. License: Public Domain: No Known Copyright
- Pendentive and Dome. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Pendentive_and_Dome.png. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Forces and Torques in Muscles and Joints. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42175/latest/. License: CC BY: Attribution
- muscle. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/muscle. License: CC BY-SA: Attribution-ShareAlike
- joint. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/joint. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Simple Machines. February 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42174/latest/. License: CC BY: Attribution
- Table of Mechanicks, Cyclopaedia, Volume 2. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Table_of_Mechanicks,_Cyclopaedia,_Volume_2.png. License: Public Domain: No Known Copyright
- OpenStax College, Simple Machines. February 13, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42174/latest/. License: CC BY: Attribution
- Simple Machines, Pulleys; Forces, Distances and MA. Located at: http://www.youtube.com/watch?v=BJ9MELhhW6U. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Arch. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Arch. License: Public Domain: No Known Copyright
- Pendentive and Dome. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Pendentive_and_Dome.png. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Forces and Torques in Muscles and Joints. February 23, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42175/latest/. License: CC BY: Attribution

