Angular Momentum (Exercises)
- Last updated
- Save as PDF
- Page ID
- 18014
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
11.1 Rolling Motion
- Can a round object released from rest at the top of a frictionless incline undergo rolling motion?
- A cylindrical can of radius R is rolling across a horizontal surface without slipping. (a) After one complete revolution of the can, what is the distance that its center of mass has moved? (b) Would this distance be greater or smaller if slipping occurred?
- A wheel is released from the top on an incline. Is the wheel most likely to slip if the incline is steep or gently sloped?
- Which rolls down an inclined plane faster, a hollow cylinder or a solid sphere? Both have the same mass and radius.
- A hollow sphere and a hollow cylinder of the same radius and mass roll up an incline without slipping and have the same initial center of mass velocity. Which object reaches a greater height before stopping?
11.2 Angular Momentum
- Can you assign an angular momentum to a particle without first defining a reference point?
- For a particle traveling in a straight line, are there any points about which the angular momentum is zero? Assume the line intersects the origin.
- Under what conditions does a rigid body have angular momentum but not linear momentum?
- If a particle is moving with respect to a chosen origin it has linear momentum. What conditions must exist for this particle’s angular momentum to be zero about the chosen origin?
- If you know the velocity of a particle, can you say anything about the particle’s angular momentum?
11.3 Conservation of Angular Momentum
- What is the purpose of the small propeller at the back of a helicopter that rotates in the plane perpendicular to the large propeller?
- Suppose a child walks from the outer edge of a rotating merry-go-round to the inside. Does the angular velocity of the merry-go-round increase, decrease, or remain the same? Explain your answer. Assume the merry-go-round is spinning without friction.
- As the rope of a tethered ball winds around a pole, what happens to the angular velocity of the ball?
- Suppose the polar ice sheets broke free and floated toward Earth’s equator without melting. What would happen to Earth’s angular velocity?
- Explain why stars spin faster when they collapse.
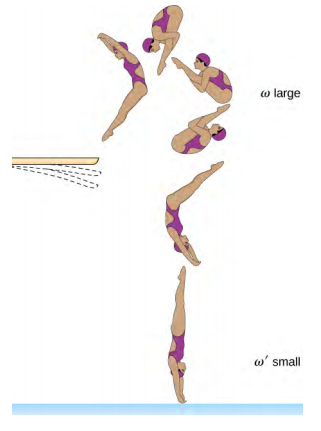
- Competitive divers pull their limbs in and curl up their bodies when they do flips. Just before entering the water, they fully extend their limbs to enter straight down (see below). Explain the effect of both actions on their angular velocities. Also explain the effect on their angular momentum.
11.4 Precession of a Gyroscope
- Gyroscopes used in guidance systems to indicate directions in space must have an angular momentum that does not change in direction. When placed in the vehicle, they are put in a compartment that is separated from the main fuselage, such that changes in the orientation of the fuselage does not affect the orientation of the gyroscope. If the space vehicle is subjected to large forces and accelerations how can the direction of the gyroscopes angular momentum be constant at all times?
- Earth precesses about its vertical axis with a period of 26,000 years. Discuss whether Equation 11.12 can be used to calculate the precessional angular velocity of Earth.
Problems
11.1 Rolling Motion
- What is the angular velocity of a 75.0-cm-diameter tire on an automobile traveling at 90.0 km/h?
- A boy rides his bicycle 2.00 km. The wheels have radius 30.0 cm. What is the total angle the tires rotate through during his trip?
- If the boy on the bicycle in the preceding problem accelerates from rest to a speed of 10.0 m/s in 10.0 s, what is the angular acceleration of the tires?
- Formula One race cars have 66-cm-diameter tires. If a Formula One averages a speed of 300 km/h during a race, what is the angular displacement in revolutions of the wheels if the race car maintains this speed for 1.5 hours?
- A marble rolls down an incline at 30° from rest. (a) What is its acceleration? (b) How far does it go in 3.0 s?
- Repeat the preceding problem replacing the marble with a solid cylinder. Explain the new result.
- A rigid body with a cylindrical cross-section is released from the top of a 30° incline. It rolls 10.0 m to the bottom in 2.60 s. Find the moment of inertia of the body in terms of its mass m and radius r.
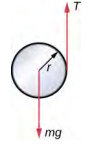
- A yo-yo can be thought of a solid cylinder of mass m and radius r that has a light string wrapped around its circumference (see below). One end of the string is held fixed in space. If the cylinder falls as the string unwinds without slipping, what is the acceleration of the cylinder?
- A solid cylinder of radius 10.0 cm rolls down an incline with slipping. The angle of the incline is 30°. The coefficient of kinetic friction on the surface is 0.400. What is the angular acceleration of the solid cylinder? What is the linear acceleration?
- A bowling ball rolls up a ramp 0.5 m high without slipping to storage. It has an initial velocity of its center of mass of 3.0 m/s. (a) What is its velocity at the top of the ramp? (b) If the ramp is 1 m high does it make it to the top?
- A 40.0-kg solid cylinder is rolling across a horizontal surface at a speed of 6.0 m/s. How much work is required to stop it?
- A 40.0-kg solid sphere is rolling across a horizontal surface with a speed of 6.0 m/s. How much work is required to stop it? Compare results with the preceding problem.
- A solid cylinder rolls up an incline at an angle of 20°. If it starts at the bottom with a speed of 10 m/s, how far up the incline does it travel?
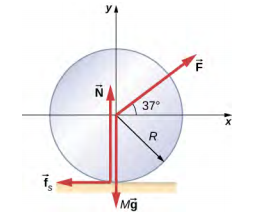
- A solid cylindrical wheel of mass M and radius R is pulled by a force \(\vec{F}\) applied to the center of the wheel at 37° to the horizontal (see the following figure). If the wheel is to roll without slipping, what is the maximum value of \(|\vec{F}|\) ? The coefficients of static and kinetic friction are \(\mu_{S}\) = 0.40 and \(\mu_{k}\) = 0.30.
- A hollow cylinder that is rolling without slipping is given a velocity of 5.0 m/s and rolls up an incline to a vertical height of 1.0 m. If a hollow sphere of the same mass and radius is given the same initial velocity, how high vertically does it roll up the incline?
11.2 Angular Momentum
- A 0.2-kg particle is travelling along the line y = 2.0 m with a velocity 5.0 m/s. What is the angular momentum of the particle about the origin?
- A bird flies overhead from where you stand at an altitude of 300.0 m and at a speed horizontal to the ground of 20.0 m/s. The bird has a mass of 2.0 kg. The radius vector to the bird makes an angle \(\theta\) with respect to the ground. The radius vector to the bird and its momentum vector lie in the xy-plane. What is the bird’s angular momentum about the point where you are standing?
- A Formula One race car with mass 750.0 kg is speeding through a course in Monaco and enters a circular turn at 220.0 km/h in the counterclockwise direction about the origin of the circle. At another part of the course, the car enters a second circular turn at 180 km/h also in the counterclockwise direction. If the radius of curvature of the first turn is 130.0 m and that of the second is 100.0 m, compare the angular momenta of the race car in each turn taken about the origin of the circular turn.
- A particle of mass 5.0 kg has position vector \(\vec{r}\) = (2.0 \(\hat{i}\) − 3.0 \(\hat{j}\))m at a particular instant of time when its velocity is \(\vec{v}\) = (3.0 \(\hat{i}\))m/s with respect to the origin. (a) What is the angular momentum of the particle? (b) If a force \(\vec{F}\) = 5.0 \(\hat{j}\) N acts on the particle at this instant, what is the torque about the origin?
- Use the right-hand rule to determine the directions of the angular momenta about the origin of the particles as shown below. The z-axis is out of the page.
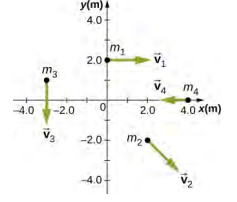
- Suppose the particles in the preceding problem have masses m1 = 0.10 kg, m2 = 0.20 kg, m3 = 0.30 kg, m4 = 0.40 kg. The velocities of the particles are v1 = 2.0 \(\hat{i}\) m/s, v2 = (3.0 \(\hat{i}\) − 3.0 \(\hat{j}\))m/s, v3 = −1.5 \(\hat{j}\) m/s, v4 = −4.0 \(\hat{i}\) m/s. (a) Calculate the angular momentum of each particle about the origin. (b) What is the total angular momentum of the four-particle system about the origin?
- Two particles of equal mass travel with the same speed in opposite directions along parallel lines separated by a distance d. Show that the angular momentum of this two-particle system is the same no matter what point is used as the reference for calculating the angular momentum.
- An airplane of mass 4.0 x 104 kg flies horizontally at an altitude of 10 km with a constant speed of 250 m/s relative to Earth. (a) What is the magnitude of the airplane’s angular momentum relative to a ground observer directly below the plane? (b) Does the angular momentum change as the airplane flies along its path?
- At a particular instant, a 1.0-kg particle’s position is \(\vec{r}\) = (2.0 \(\hat{i}\) − 4.0 \(\hat{j}\) + 6.0 \(\hat{k}\))m, its velocity is \(\vec{v}\) = (−1.0 \(\hat{i}\) + 4.0 \(\hat{j}\) + 1.0 \(\hat{k}\))m/s, and the force on it is \(\vec{F}\) = (10.0 \(\hat{i}\) + 15.0 \(\hat{j}\))N. (a) What is the angular momentum of the particle about the origin? (b) What is the torque on the particle about the origin? (c) What is the time rate of change of the particle’s angular momentum at this instant?
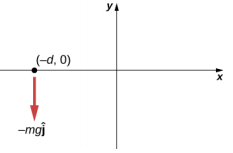
- A particle of mass m is dropped at the point (−d, 0) and falls vertically in Earth’s gravitational field −g \(\hat{j}\). (a) What is the expression for the angular momentum of the particle around the z-axis, which points directly out of the page as shown below? (b) Calculate the torque on the particle around the z-axis. (c) Is the torque equal to the time rate of change of the angular momentum?
- (a) Calculate the angular momentum of Earth in its orbit around the Sun. (b) Compare this angular momentum with the angular momentum of Earth about its axis.
- A boulder of mass 20 kg and radius 20 cm rolls down a hill 15 m high from rest. What is its angular momentum when it is half way down the hill? (b) At the bottom?
- A satellite is spinning at 6.0 rev/s. The satellite consists of a main body in the shape of a sphere of radius 2.0 m and mass 10,000 kg, and two antennas projecting out from the center of mass of the main body that can be approximated with rods of length 3.0 m each and mass 10 kg. The antenna’s lie in the plane of rotation. What is the angular momentum of the satellite?
- A propeller consists of two blades each 3.0 m in length and mass 120 kg each. The propeller can be approximated by a single rod rotating about its center of mass. The propeller starts from rest and rotates up to 1200 rpm in 30 seconds at a constant rate. (a) What is the angular momentum of the propeller at t = 10 s; t = 20 s? (b) What is the torque on the propeller?
- A pulsar is a rapidly rotating neutron star. The Crab nebula pulsar in the constellation Taurus has a period of 33.5 x 10−3 s, radius 10.0 km, and mass 2.8 x 1030 kg. The pulsar’s rotational period will increase over time due to the release of electromagnetic radiation, which doesn’t change its radius but reduces its rotational energy. (a) What is the angular momentum of the pulsar? (b) Suppose the angular velocity decreases at a rate of 10−14 rad/s2. What is the torque on the pulsar?
- The blades of a wind turbine are 30 m in length and rotate at a maximum rotation rate of 20 rev/min. (a) If the blades are 6000 kg each and the rotor assembly has three blades, calculate the angular momentum of the turbine at this rotation rate. (b) What is the torque require to rotate the blades up to the maximum rotation rate in 5 minutes?
- A roller coaster has mass 3000.0 kg and needs to make it safely through a vertical circular loop of radius 50.0 m. What is the minimum angular momentum of the coaster at the bottom of the loop to make it safely through? Neglect friction on the track. Take the coaster to be a point particle.
- A mountain biker takes a jump in a race and goes airborne. The mountain bike is traveling at 10.0 m/s before it goes airborne. If the mass of the front wheel on the bike is 750 g and has radius 35 cm, what is the angular momentum of the spinning wheel in the air the moment the bike leaves the ground?
11.3 Conservation of Angular Momentum
- A disk of mass 2.0 kg and radius 60 cm with a small mass of 0.05 kg attached at the edge is rotating at 2.0 rev/s. The small mass suddenly separates from the disk. What is the disk’s final rotation rate?
- The Sun’s mass is 2.0 x 1030 kg, its radius is 7.0 x 105 km, and it has a rotational period of approximately 28 days. If the Sun should collapse into a white dwarf of radius 3.5 x 103 km, what would its period be if no mass were ejected and a sphere of uniform density can model the Sun both before and after?
- A cylinder with rotational inertia I1 = 2.0 kg • m2 rotates clockwise about a vertical axis through its center with angular speed \(\omega_{1}\) = 5.0 rad/s. A second cylinder with rotational inertia I2 = 1.0 kg • m2 rotates counterclockwise about the same axis with angular speed \(\omega_{2}\) = 8.0 rad/s. If the cylinders couple so they have the same rotational axis what is the angular speed of the combination? What percentage of the original kinetic energy is lost to friction?
- A diver off the high board imparts an initial rotation with his body fully extended before going into a tuck and executing three back somersaults before hitting the water. If his moment of inertia before the tuck is 16.9 kg • m2 and after the tuck during the somersaults is 4.2 kg • m2, what rotation rate must he impart to his body directly off the board and before the tuck if he takes 1.4 s to execute the somersaults before hitting the water?
- An Earth satellite has its apogee at 2500 km above the surface of Earth and perigee at 500 km above the surface of Earth. At apogee its speed is 730 m/s. What is its speed at perigee? Earth’s radius is 6370 km (see below).
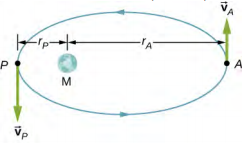
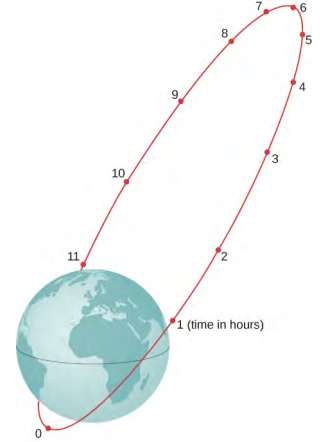
- A Molniya orbit is a highly eccentric orbit of a communication satellite so as to provide continuous communications coverage for Scandinavian countries and adjacent Russia. The orbit is positioned so that these countries have the satellite in view for extended periods in time (see below). If a satellite in such an orbit has an apogee at 40,000.0 km as measured from the center of Earth and a velocity of 3.0 km/s, what would be its velocity at perigee measured at 200.0 km altitude?
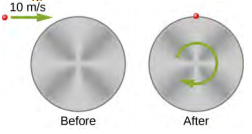
- Shown below is a small particle of mass 20 g that is moving at a speed of 10.0 m/s when it collides and sticks to the edge of a uniform solid cylinder. The cylinder is free to rotate about its axis through its center and is perpendicular to the page. The cylinder has a mass of 0.5 kg and a radius of 10 cm, and is initially at rest. (a) What is the angular velocity of the system after the collision? (b) How much kinetic energy is lost in the collision?
- A bug of mass 0.020 kg is at rest on the edge of a solid cylindrical disk (M = 0.10 kg, R = 0.10 m) rotating in a horizontal plane around the vertical axis through its center. The disk is rotating at 10.0 rad/s. The bug crawls to the center of the disk. (a) What is the new angular velocity of the disk? (b) What is the change in the kinetic energy of the system? (c) If the bug crawls back to the outer edge of the disk, what is the angular velocity of the disk then? (d) What is the new kinetic energy of the system? (e) What is the cause of the increase and decrease of kinetic energy?
- A uniform rod of mass 200 g and length 100 cm is free to rotate in a horizontal plane around a fixed vertical axis through its center, perpendicular to its length. Two small beads, each of mass 20 g, are mounted in grooves along the rod. Initially, the two beads are held by catches on opposite sides of the rod’s center, 10 cm from the axis of rotation. With the beads in this position, the rod is rotating with an angular velocity of 10.0 rad/s. When the catches are released, the beads slide outward along the rod. (a) What is the rod’s angular velocity when the beads reach the ends of the rod? (b) What is the rod’s angular velocity if the beads fly off the rod?
- A merry-go-round has a radius of 2.0 m and a moment of inertia 300 kg • m2. A boy of mass 50 kg runs tangent to the rim at a speed of 4.0 m/s and jumps on. If the merry-go-round is initially at rest, what is the angular velocity after the boy jumps on?
- A playground merry-go-round has a mass of 120 kg and a radius of 1.80 m and it is rotating with an angular velocity of 0.500 rev/s. What is its angular velocity after a 22.0-kg child gets onto it by grabbing its outer edge? The child is initially at rest.
- Three children are riding on the edge of a merry-go-round that is 100 kg, has a 1.60-m radius, and is spinning at 20.0 rpm. The children have masses of 22.0, 28.0, and 33.0 kg. If the child who has a mass of 28.0 kg moves to the center of the merry-go-round, what is the new angular velocity in rpm?
- (a) Calculate the angular momentum of an ice skater spinning at 6.00 rev/s given his moment of inertia is 0.400 kg • m2. (b) He reduces his rate of spin (his angular velocity) by extending his arms and increasing his moment of inertia. Find the value of his moment of inertia if his angular velocity decreases to 1.25 rev/s. (c) Suppose instead he keeps his arms in and allows friction of the ice to slow him to 3.00 rev/s. What average torque was exerted if this takes 15.0 s?
- Twin skaters approach one another as shown below and lock hands. (a) Calculate their final angular velocity, given each had an initial speed of 2.50 m/s relative to the ice. Each has a mass of 70.0 kg, and each has a center of mass located 0.800 m from their locked hands. You may approximate their moments of inertia to be that of point masses at this radius. (b) Compare the initial kinetic energy and final kinetic energy.
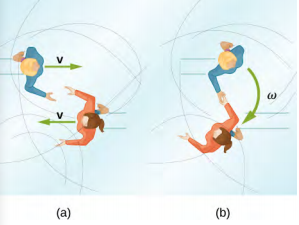
- A baseball catcher extends his arm straight up to catch a fast ball with a speed of 40 m/s. The baseball is 0.145 kg and the catcher’s arm length is 0.5 m and mass 4.0 kg. (a) What is the angular velocity of the arm immediately after catching the ball as measured from the arm socket? (b) What is the torque applied if the catcher stops the rotation of his arm 0.3 s after catching the ball?
- In 2015, in Warsaw, Poland, Olivia Oliver of Nova Scotia broke the world record for being the fastest spinner on ice skates. She achieved a record 342 rev/min, beating the existing Guinness World Record by 34 rotations. If an ice skater extends her arms at that rotation rate, what would be her new rotation rate? Assume she can be approximated by a 45-kg rod that is 1.7 m tall with a radius of 15 cm in the record spin. With her arms stretched take the approximation of a rod of length 130 cm with 10% of her body mass aligned perpendicular to the spin axis. Neglect frictional forces.
- A satellite in a geosynchronous circular orbit is 42,164.0 km from the center of Earth. A small asteroid collides with the satellite sending it into an elliptical orbit of apogee 45,000.0 km. What is the speed of the satellite at apogee? Assume its angular momentum is conserved.
- A gymnast does cartwheels along the floor and then launches herself into the air and executes several flips in a tuck while she is airborne. If her moment of inertia when executing the cartwheels is 13.5 kg • m2 and her spin rate is 0.5 rev/s, how many revolutions does she do in the air if her moment of inertia in the tuck is 3.4 kg • m2 and she has 2.0 s to do the flips in the air?
- The centrifuge at NASA Ames Research Center has a radius of 8.8 m and can produce forces on its payload of 20 gs or 20 times the force of gravity on Earth. (a) What is the angular momentum of a 20-kg payload that experiences 10 gs in the centrifuge? (b) If the driver motor was turned off in (a) and the payload lost 10 kg, what would be its new spin rate, taking into account there are no frictional forces present?
- A ride at a carnival has four spokes to which pods are attached that can hold two people. The spokes are each 15 m long and are attached to a central axis. Each spoke has mass 200.0 kg, and the pods each have mass 100.0 kg. If the ride spins at 0.2 rev/s with each pod containing two 50.0-kg children, what is the new spin rate if all the children jump off the ride?
- An ice skater is preparing for a jump with turns and has his arms extended. His moment of inertia is 1.8 kg • m2 while his arms are extended, and he is spinning at 0.5 rev/s. If he launches himself into the air at 9.0 m/s at an angle of 45° with respect to the ice, how many revolutions can he execute while airborne if his moment of inertia in the air is 0.5 kg • m2?
- A space station consists of a giant rotating hollow cylinder of mass 106 kg including people on the station and a radius of 100.00 m. It is rotating in space at 3.30 rev/min in order to produce artificial gravity. If 100 people of an average mass of 65.00 kg spacewalk to an awaiting spaceship, what is the new rotation rate when all the people are off the station?
- Neptune has a mass of 1.0 x 1026 kg and is 4.5 x 109 km from the Sun with an orbital period of 165 years. Planetesimals in the outer primordial solar system 4.5 billion years ago coalesced into Neptune over hundreds of millions of years. If the primordial disk that evolved into our present day solar system had a radius of 1011 km and if the matter that made up these planetesimals that later became Neptune was spread out evenly on the edges of it, what was the orbital period of the outer edges of the primordial disk?
11.4 Precession of a Gyroscope
- A gyroscope has a 0.5-kg disk that spins at 40 rev/s. The center of mass of the disk is 10 cm from a pivot which is also the radius of the disk. What is the precession angular velocity?
- The precession angular velocity of a gyroscope is 1.0 rad/s. If the mass of the rotating disk is 0.4 kg and its radius is 30 cm, as well as the distance from the center of mass to the pivot, what is the rotation rate in rev/s of the disk?
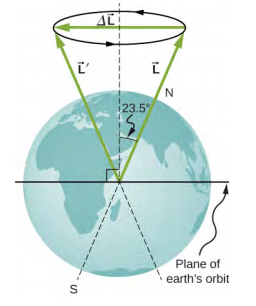
- The axis of Earth makes a 23.5° angle with a direction perpendicular to the plane of Earth’s orbit. As shown below, this axis precesses, making one complete rotation in 25,780 y. (a) Calculate the change in angular momentum in half this time. (b) What is the average torque producing this change in angular momentum? (c) If this torque were created by a pair of forces acting at the most effective point on the equator, what would the magnitude of each force be?
Additional Problems
- A marble is rolling across the floor at a speed of 7.0 m/ s when it starts up a plane inclined at 30° to the horizontal. (a) How far along the plane does the marble travel before coming to a rest? (b) How much time elapses while the marble moves up the plane?
- Repeat the preceding problem replacing the marble with a hollow sphere. Explain the new results.
- The mass of a hoop of radius 1.0 m is 6.0 kg. It rolls across a horizontal surface with a speed of 10.0 m/s. (a) How much work is required to stop the hoop? (b) If the hoop starts up a surface at 30° to the horizontal with a speed of 10.0 m/s, how far along the incline will it travel before stopping and rolling back down?
- Repeat the preceding problem for a hollow sphere of the same radius and mass and initial speed. Explain the differences in the results.
- A particle has mass 0.5 kg and is traveling along the line x = 5.0 m at 2.0 m/s in the positive y-direction. What is the particle’s angular momentum about the origin?
- A 4.0-kg particle moves in a circle of radius 2.0 m. The angular momentum of the particle varies in time according to l = 5.0t2. (a) What is the torque on the particle about the center of the circle at t = 3.4 s? (b) What is the angular velocity of the particle at t = 3.4 s?
- A proton is accelerated in a cyclotron to 5.0 x 106 m/s in 0.01 s. The proton follows a circular path. If the radius of the cyclotron is 0.5 km, (a) What is the angular momentum of the proton about the center at its maximum speed? (b) What is the torque on the proton about the center as it accelerates to maximum speed?
- (a) What is the angular momentum of the Moon in its orbit around Earth? (b) How does this angular momentum compare with the angular momentum of the Moon on its axis? Remember that the Moon keeps one side toward Earth at all times.
- A DVD is rotating at 500 rpm. What is the angular momentum of the DVD if has a radius of 6.0 cm and mass 20.0 g?
- A potter’s disk spins from rest up to 10 rev/s in 15 s. The disk has a mass 3.0 kg and radius 30.0 cm. What is the angular momentum of the disk at t = 5 s, t = 10 s?
- Suppose you start an antique car by exerting a force of 300 N on its crank for 0.250 s. What is the angular momentum given to the engine if the handle of the crank is 0.300 m from the pivot and the force is exerted to create maximum torque the entire time?
- A solid cylinder of mass 2.0 kg and radius 20 cm is rotating counterclockwise around a vertical axis through its center at 600 rev/min. A second solid cylinder of the same mass is rotating clockwise around the same vertical axis at 900 rev/min. If the cylinders couple so that they rotate about the same vertical axis, what is the angular velocity of the combination?
- A boy stands at the center of a platform that is rotating without friction at 1.0 rev/s. The boy holds weights as far from his body as possible. At this position the total moment of inertia of the boy, platform, and weights is 5.0 kg • m2. The boy draws the weights in close to his body, thereby decreasing the total moment of inertia to 1.5 kg • m2. (a) What is the final angular velocity of the platform? (b) By how much does the rotational kinetic energy increase?
- Eight children, each of mass 40 kg, climb on a small merry-go-round. They position themselves evenly on the outer edge and join hands. The merry-go-round has a radius of 4.0 m and a moment of inertia 1000.0 kg • m2. After the merry-go-round is given an angular velocity of 6.0 rev/min, the children walk inward and stop when they are 0.75 m from the axis of rotation. What is the new angular velocity of the merry-go-round? Assume there is negligible frictional torque on the structure.
- A thin meter stick of mass 150 g rotates around an axis perpendicular to the stick’s long axis at an angular velocity of 240 rev/min. What is the angular momentum of the stick if the rotation axis (a) passes through the center of the stick? (b) Passes through one end of the stick?
- A satellite in the shape of a sphere of mass 20,000 kg and radius 5.0 m is spinning about an axis through its center of mass. It has a rotation rate of 8.0 rev/s. Two antennas deploy in the plane of rotation extending from the center of mass of the satellite. Each antenna can be approximated as a rod has mass 200.0 kg and length 7.0 m. What is the new rotation rate of the satellite?
- A top has moment of inertia 3.2 x 10−4 kg • m2 and radius 4.0 cm from the center of mass to the pivot point. If it spins at 20.0 rev/s and is precessing, how many revolutions does it precess in 10.0 s?
Challenge Problems
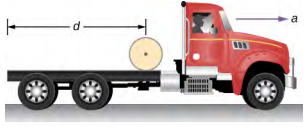
- The truck shown below is initially at rest with solid cylindrical roll of paper sitting on its bed. If the truck moves forward with a uniform acceleration a, what distance s does it move before the paper rolls off its back end? (Hint: If the roll accelerates forward with a′, then is accelerates backward relative to the truck with an acceleration a − a′. Also, R\(\alpha\) = a − a′.)
- A bowling ball of radius 8.5 cm is tossed onto a bowling lane with speed 9.0 m/s. The direction of the toss is to the left, as viewed by the observer, so the bowling ball starts to rotate counterclockwise when in contact with the floor. The coefficient of kinetic friction on the lane is 0.3. (a) What is the time required for the ball to come to the point where it is not slipping? What is the distance d to the point where the ball is rolling without slipping?
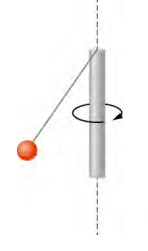
- A small ball of mass 0.50 kg is attached by a massless string to a vertical rod that is spinning as shown below. When the rod has an angular velocity of 6.0 rad/s, the string makes an angle of 30° with respect to the vertical. (a) If the angular velocity is increased to 10.0 rad/s, what is the new angle of the string? (b) Calculate the initial and final angular momenta of the ball. (c) Can the rod spin fast enough so that the ball is horizontal?
- A bug flying horizontally at 1.0 m/s collides and sticks to the end of a uniform stick hanging vertically. After the impact, the stick swings out to a maximum angle of 5.0° from the vertical before rotating back. If the mass of the stick is 10 times that of the bug, calculate the length of the stick.
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


