11.4: Thermal Expansion
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18034

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Describe volume changes that take place in response to a temperature change
Thermal expansion is the tendency of matter to change in volume in response to a change in temperature. (An example of this is the buckling of railroad track, as seen in. ) Atoms and molecules in a solid, for instance, constantly oscillate around its equilibrium point. This kind of excitation is called thermal motion. When a substance is heated, its constituent particles begin moving more, thus maintaining a greater average separation with their neighboring particles. The degree of expansion divided by the change in temperature is called the material’s coefficient of thermal expansion; it generally varies with temperature.

Fig 1: Thermal expansion of long continuous sections of rail tracks is the driving force for rail buckling. This phenomenon resulted in 190 train derailments during 1998–2002 in the US alone.
Thermal Expansion: A brief introduction to thermal expansion for students.
Expansion, Not Contraction
Why does matter usually expand when heated? The answer can be found in the shape of the typical particle-particle potential in matter. Particles in solids and liquids constantly feel the presence of other neighboring particles. This interaction can be represented mathematically as a potential curve. Fig 2 illustrates how this inter-particle potential usually takes an asymmetric form rather than a symmetric form, as a function of particle-particle distance. Note that the potential curve is steeper for shorter distance. In the diagram, (b) shows that as the substance is heated, the equilibrium (or average) particle-particle distance increases. Materials which contract or maintain their shape with increasing temperature are rare. This effect is limited in size, and only occurs within limited temperature ranges.
Fig 2: Typical inter-particle potential in condensed matter (such as solid or liquid).
Linear Expansion
To a first approximation, the change in length measurements of an object (lineardimension as opposed to, for example, volumetric dimension) due to thermal expansion is related to temperature change by a linear expansion coefficient. It is the fractional change in length per degree of temperature change. Assuming negligible effect of pressure, we may write:
αL=1LdLdT,
where L is a particular length measurement and dLdT is the rate of change of that linear dimension per unit change in temperature. From the definition of the expansion coefficient, the change in the linear dimension ΔL over a temperature range ΔT can be estimated to be:
ΔLL=αLΔT.
This equation works well as long as the linear-expansion coefficient does not change much over the change in temperature. If it does, the equation must be integrated.
Area Expansion
Objects expand in all dimensions. That is, their areas and volumes, as well as their lengths, increase with temperature.
learning objectives
- Express the area thermal expansion coefficient in the form of an equation
We learned about the linear expansion (in one dimension) in the previous Atom. Objects expand in all dimensions, and we can extend the thermal expansion for 1D to two (or three) dimensions. That is, their areas and volumes, as well as their lengths, increase with temperature.
Quiz
Before we look into details, here is an interesting question. Imagine that we have a rectangular sheet of metal with a circular hole in the middle. If the metal is heated, we can guess that the the piece, in general, will get larger due to thermal expansion. Now, what is going to happen with the circular hole in the middle? Is the hole going to be larger or smaller? Answer: Imagine that we have a similar metal sheet but without a hole. Draw an imaginary circular line representing the circular hole in our quiz. How does this imaginary circle change as the metal is heated? Yes. It will get bigger. Therefore, you can guess that the hole in our quiz will get larger.
Fig 1: In general, objects expand in all directions as temperature increases. In these drawings, the original boundaries of the objects are shown with solid lines, and the expanded boundaries with dashed lines. (a) Area increases because both length and width increase. The area of a circular plug also increases. (b) If the plug is removed, the hole it leaves becomes larger with increasing temperature, just as if the expanding plug were still in place.
Area thermal expansion coefficient
The area thermal expansion coefficient relates the change in a material’s area dimensions to a change in temperature. It is the fractional change in area per degree of temperature change. Ignoring pressure, we may write: αA=1AdAdT, where is some area of interest on the object, and dAdT is the rate of change of that area per unit change in temperature. The change in the linear dimension can be estimated as: ΔAA=αAΔT. This equation works well as long as the linear expansion coefficient does not change much over the change in temperature ΔT. If it does, the equation must be integrated.
Relationship to linear thermal expansion coefficient
For isotropic materials, and for small expansions, the linear thermal expansion coefficient is one half of the area coefficient. To derive the relationship, let’s take a square of steel that has sides of length L. The original area will be A=L2,and the new area, after a temperature increase, will be
A+ΔA=(L+ΔL)2=L2+2LΔL+(ΔL)2≈L2+2LΔL=A+2AΔLL
The approximation holds for a sufficiently small ΔL campared to L. Since ΔAA=2ΔLL from the equation above (and from the definitions of the thermal coefficients), we get αA=2αL.
Volume Expansion
Substances expand or contract when their temperature changes, with expansion or contraction occurring in all directions.
learning objectives
- Compare the effects of the pressure on the expansion of gaseous and solid materials
The volumetric thermal expansion coefficient is the most basic thermal expansion coefficient. illustrates that, in general, substances expand or contract when their temperature changes, with expansion or contraction occurring in all directions. Such substances that expand in all directions are called isotropic. For isotropic materials, the area and linear coefficients may be calculated from the volumetric coefficient (discussed below).
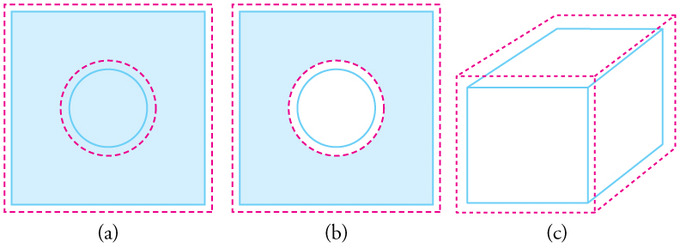
Volumetric Expansion: In general, objects expand in all directions as temperature increases. In these drawings, the original boundaries of the objects are shown with solid lines, and the expanded boundaries with dashed lines. (a) Area increases because both length and width increase. The area of a circular plug also increases. (b) If the plug is removed, the hole it leaves becomes larger with increasing temperature, just as if the expanding plug were still in place. (c) Volume also increases, because all three dimensions increase.
Thermal Expansion – Volume Expansion: A brief introduction to thermal expansion for students.
Mathematical definitions of these coefficients are defined below for solids, liquids, and gasses:
αV=1V(∂V∂T)p.
The subscript p indicates that the pressure is held constant during the expansion. In the case of a gas, the fact that the pressure is held constant is important, as the volume of a gas will vary appreciably with pressure as well as with temperature.
For a solid, we can ignore the effects of pressure on the material, thus the volumetric thermal expansion coefficient can be written:
αV=1VdVdT,
where V is the volume of the material, and is dV/dT the rate of change of that volume with temperature. This means that the volume of a material changes by some fixed fractional amount. For example, a steel block with a volume of 1 cubic meter might expand to 1.002 cubic meters when the temperature is raised by 50 °C. This is an expansion of 0.2%. The volumetric expansion coefficient would be 0.2% for 50 °C, or 0.004% per degree C.
Relationship to Linear Thermal Expansion Coefficient
For isotropic material, and for small expansions, the linear thermal expansion coefficient is one third the volumetric coefficient. To derive the relationship, let’s take a cube of steel that has sides of length L. The original volume will be V=L3,and the new volume, after a temperature increase, will be:
V+ΔV=(L+ΔL)3=L3+3L2ΔL+3L(ΔL)2+(ΔL)3≈L3+3L2ΔL=V+3VΔLL.
The approximation holds for a sufficiently small ΔL compared to L. Since:
ΔVV=3ΔLL
(and from the definitions of the thermal coefficients), we arrive at:
αV=3αL
Special Properties of Water
Objects will expand with increasing temperature, but water is the most important exception to the general rule.
learning objectives
- Describe thermal expansion properties of water
Special Properties of Water
In general, objects will expand with increasing temperature. However, a number of materials contract on heating within certain temperature ranges; this is usually called negative thermal expansion, rather than “thermal contraction. ” Water is the most important exception to the general rule. Water has this unique characteristic because of the particular nature of the hydrogen bond in H2O.
Density of Water as Temperature Changes
At temperatures greater than 4ºC (40ºF) water expands with increasing temperature (its density decreases). However, it expands with decreasing temperature when it is between +4ºC and 0ºC (40ºF to 32ºF). Water is densest at +4ºC.
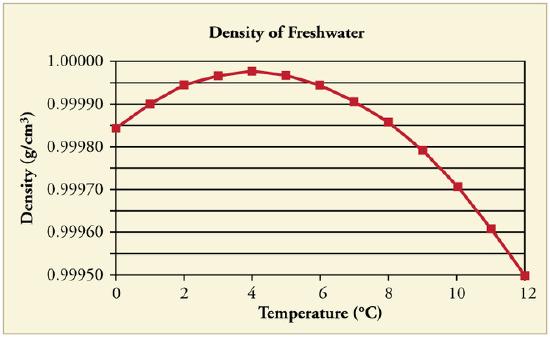
Water Density vs. Temperature: The density of water as a function of temperature. Note that the thermal expansion is actually very small. The maximum density at +4ºC is only 0.0075% greater than the density at 2ºC, and 0.012% greater than that at 0ºC.
Perhaps the most striking effect of this phenomenon is the freezing of water in a pond. When water near the surface cools down to 4ºC it is denser than the remaining water and thus will sink to the bottom. This “turnover” results in a layer of warmer water near the surface, which is then cooled. Eventually the pond has a uniform temperature of 4ºC. If the temperature in the surface layer drops below 4ºC, the water is less dense than the water below, and thus stays near the top.
As a result, the pond surface can completely freeze over, while the bottom may remain at 4ºC. The ice on top of liquid water provides an insulating layer from winter’s harsh exterior air temperatures. Fish and other aquatic life can survive in 4ºC water beneath ice, due to this unusual characteristic of water. It also produces circulation of water in the pond that is necessary for a healthy ecosystem of the body of water.
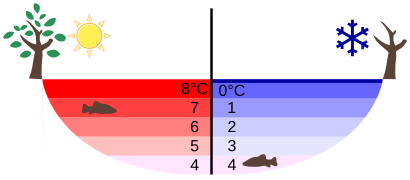
Temperature in a Lake: Temperature distribution in a lake on warm and cold days in winter
Ice Versus Water
The solid form of most substances is denser than the liquid phase; thus, a block of most solids will sink in the liquid. However, a block of ice floats in liquid water because ice is less dense. Upon freezing, the density of water decreases by about 9%.
Key Points
- Inter-particle potential usually takes an asymmetric form, rather than a symmetric form as a function of particle-particle distance. This is why matters expands and contracts as temperature changes.
- The change in length measurements of an object due to thermal expansion is related to temperature change by a “linear expansion coefficient”, which is given as αL=1LdLdT.
- The linear expansion coefficient is as an approximation over a narrow temperature interval only.
- The area thermal expansion coefficient relates the change in a material’s area dimensions to a change in temperature. It is defined as αA=1AdAdT.
- The relationship between the area and linear thermal expansion coefficient is given as the following: αA=2αL.
- Just like the linear expansion coefficient, the area thermal expansion coefficient works as an approximation over a narrow temperature interval only.
- Substances that expand at the same rate in every direction are called isotropic.
- In the case of a gas, expansion depends on how the pressure changed in the process because the volume of a gas will vary appreciably with pressure as well as temperature.
- For a solid, we can ignore the effects of pressure on the material, and the volumetric thermal expansion coefficient can be written as αV=1VdVdT. For isotropic materials, αV=3αL.
- Water expands with increasing temperature (its density decreases) when it is at temperatures greater than 4ºC (40ºF). However, it expands with decreasing temperature when it is between +4ºC and 0ºC (40ºF to 32ºF). Water is densest at +4ºC.
- Due to the peculiar thermal expansion property of water, a pond surface can completely freeze over, while the bottom may remain at 4ºC. Fish and other aquatic life can survive in 4ºC water beneath ice, due to this unusual characteristic of water.
- The solid form of most substances is denser than the liquid phase; thus, a block of most solids will sink in the liquid. However, a block of ice floats in liquid water because ice is less dense.
Key Terms
- potential: A curve describing the situation where the difference in the potential energies of an object in two different positions depends only on those positions.
- linear thermal expansion coefficient: The fractional change in length per degree of temperature change.
- isotropic: Having properties that are identical in all directions; exhibiting isotropy.
- hydrogen bond: A weak bond in which a hydrogen atom in one molecule is attracted to an electronegative atom (usually nitrogen or oxygen) in the same or different molecule.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Thermal expansion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thermal_expansion. License: CC BY-SA: Attribution-ShareAlike
- potential. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/potential. License: CC BY-SA: Attribution-ShareAlike
- Thermal expansion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thermal_expansion. License: CC BY: Attribution
- Thermal Expansion. Located at: http://www.youtube.com/watch?v=3P7gHzpXpmU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/510d56c6e4b0c14bf464b1af/1.jpg. License: CC BY: Attribution
- Thermal expansion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thermal_expansion%23Area_expansion. License: CC BY-SA: Attribution-ShareAlike
- linear thermal expansion coefficient. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/linear%20thermal%20expansion%20coefficient. License: CC BY-SA: Attribution-ShareAlike
- Thermal expansion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thermal_expansion. License: CC BY: Attribution
- Thermal Expansion. Located at: http://www.youtube.com/watch?v=3P7gHzpXpmU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/510d56c6e4b0c14bf464b1af/1.jpg. License: CC BY: Attribution
- OpenStax College, Thermal Expansion of Solids and Liquids. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42215/latest/. License: CC BY: Attribution
- Thermal expansion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thermal_expansion. License: CC BY-SA: Attribution-ShareAlike
- linear thermal expansion coefficient. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/linear%20thermal%20expansion%20coefficient. License: CC BY-SA: Attribution-ShareAlike
- isotropic. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/isotropic. License: CC BY-SA: Attribution-ShareAlike
- Thermal expansion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thermal_expansion. License: CC BY: Attribution
- Thermal Expansion. Located at: http://www.youtube.com/watch?v=3P7gHzpXpmU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/510d56c6e4b0c14bf464b1af/1.jpg. License: CC BY: Attribution
- OpenStax College, Thermal Expansion of Solids and Liquids. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42215/latest/. License: CC BY: Attribution
- Thermal Expansion - Volume Expansion. Located at: http://www.youtube.com/watch?v=3P7gHzpXpmU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Thermal Expansion of Solids and Liquids. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42215/latest/. License: CC BY: Attribution
- OpenStax College, Thermal Expansion of Solids and Liquids. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42215/latest/. License: CC BY: Attribution
- Properties of water. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Properties_of_water. License: CC BY-SA: Attribution-ShareAlike
- hydrogen bond. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/hydrogen_bond. License: CC BY-SA: Attribution-ShareAlike
- Thermal expansion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thermal_expansion. License: CC BY: Attribution
- Thermal Expansion. Located at: http://www.youtube.com/watch?v=3P7gHzpXpmU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/510d56c6e4b0c14bf464b1af/1.jpg. License: CC BY: Attribution
- OpenStax College, Thermal Expansion of Solids and Liquids. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42215/latest/. License: CC BY: Attribution
- Thermal Expansion - Volume Expansion. Located at: http://www.youtube.com/watch?v=3P7gHzpXpmU. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Thermal Expansion of Solids and Liquids. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42215/latest/. License: CC BY: Attribution
- Properties of water. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Properties_of_water. License: CC BY: Attribution
- OpenStax College, Thermal Expansion of Solids and Liquids. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42215/latest/. License: CC BY: Attribution


