12.1: Introduction
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18051

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Distinguish three modes of heat transfer
Introduction to Heat and Heat Transfer
Energy can exist in many forms and heat is one of the most intriguing. Heat is often hidden, as it only exists when in transit, and is transferred by a number of distinctly different methods. Heat transfer touches every aspect of our lives and helps us understand how the universe functions. It explains the chill we feel on a clear breezy night, or why Earth’s core has yet to cool. This module defines and explores heat transfer, its effects, and the methods by which heat is transferred. These topics are fundamental, as well as practical, and will often be referred to in the modules ahead.
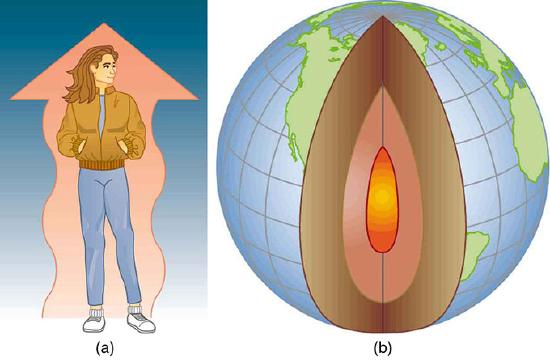
Examples of Heat Transfer: (a) The chilling effect of a clear breezy night is produced by the wind and by radiative heat transfer to cold outer space. (b) There was once great controversy about the Earth’s age, but it is now generally accepted to be about 4.5 billion years old. Much of the debate is centered on the Earth’s molten interior. According to our understanding of heat transfer, if the Earth is really that old, its center should have cooled off long ago. The discovery of radioactivity in rocks revealed the source of energy that keeps the Earth’s interior molten, despite heat transfer to the surface, and from there to cold outer space.
Definitions
Scottish physicist James Clerk Maxwell, in his 1871 classic Theory of Heat, was one of many who began to build on the already established idea that heat was something to do with matter in motion. This was the same idea put forwards by Sir Benjamin Thompson in 1798, who said he was only following on from the work of many others. One of Maxwell’s recommended books was Heat as a Mode of Motion by John Tyndall. Maxwell outlined four stipulations for the definition of heat:
- It is something which may be transferred from one body to another.
- It is a measurable quantity, and thus treated mathematically.
- It cannot be treated as a substance, because it may be transformed into something that is not a substance, such as mechanical work.
- Heat is one of the forms of energy.
In the following sections, we will define heat more rigorously, paying particular attention to how it can be measured and quantified.
Estimation of Quantity of Heat
The quantity of heat transferred by some process can either be directly measured, or determined indirectly through calculations based on other quantities. Direct measurement is by calorimetry and is the primary empirical basis of the idea of quantity of heat transferred in a process. The transferred heat is measured by changes in a body of known properties, for example, temperature rise, change in volume or length, or phase change, such as melting of ice. Indirect estimations of quantity of heat transferred rely on the law of conservation of energy, and, in particular cases, on the first law of thermodynamics (explored in the following sections). Indirect estimation is the primary approach of many theoretical studies of quantity of heat transferred.
Heat Transfer Methods
After defining and quantifying heat transfer and its effects on physical systems, we will discuss the methods by which heat is transferred. So many processes involve heat transfer, so that it is hard to imagine a situation where no heat transfer occurs. Yet every process involving heat transfer takes place by only three methods:
- Conduction is heat transfer through stationary matter by physical contact. ( The matter is stationary on a macroscopic scale—we know there is thermal motion of the atoms and molecules at any temperature above absolute zero. ) Heat transferred between the electric burner of a stove and the bottom of a pan is transferred by conduction.
- Convection is the heat transfer by the macroscopic movement of a fluid. This type of transfer takes place in a forced-air furnace and in weather systems, for example.
- Heat transfer by radiation occurs when microwaves, infrared radiation, visible light, or another form of electromagnetic radiation is emitted or absorbed. An obvious example is the warming of the Earth by the Sun. A less obvious example is thermal radiation from the human body.
Heat as Energy Transfer
Heat is the spontaneous transfer of energy due to a temperature difference.
learning objectives
- Identify SI and common units of heat
Heat as Energy Transfer
Consider two objects at different temperatures that are brought together. Energy is transferred from the hotter object to the cooler one, until both objects reach thermal equilibrium (i.e., both become the same temperature). How is this energy transferred? No work is done by either object, because no force acts through a distance. The transfer of energy is caused by the temperature difference, and ceases once the temperatures are equal. This observation leads to the following definition of heat: Heat is the spontaneous transfer of energy due to a temperature difference.
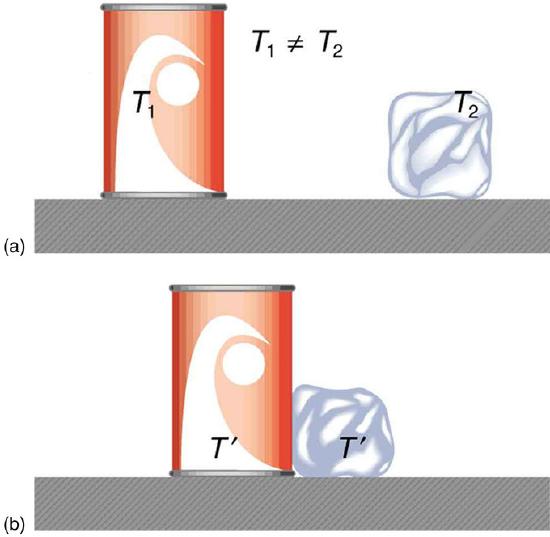
Heat Transfer and Equilibrium: (a) The soft drink and the ice have different temperatures, T1 and T2, and are not in thermal equilibrium. (b) When the soft drink and ice are allowed to interact, energy is transferred until they reach the same temperature T, achieving equilibrium. Heat transfer occurs due to the difference in temperatures. In fact, since the soft drink and ice are both in contact with the surrounding air and bench, the equilibrium temperature will be the same for both.
Where Is the Most Heat Lost?: Use movable thermometers to discover where a house has poor insulation.
Heat Transfer: A brief introduction to heat transfer for students.
Heat is often confused with temperature. For example, we may say the heat was unbearable, when we actually mean that the temperature was high. Heat is a form of energy, whereas temperature is not. The misconception arises because we are sensitive to the flow of heat, rather than the temperature.
Units
Owing to the fact that heat is a form of energy, it has the SI unit of joule (J). The calorie (cal) is a common unit of energy, defined as the energy needed to change the temperature of 1.00 g of water by 1.00ºC —specifically, between 14.5ºC and 15.5ºC, since there is a slight temperature dependence. Another common unit of heat is the kilocalorie (kcal), which is the energy needed to change the temperature of 1.00 kg of water by 1.00ºC. Since mass is often specified in kilograms, kilocalorie is commonly used. Food calories (given the notation Cal, and sometimes called “big calorie”) are actually kilocalories (1kilocalorie=1000 calories), a fact not easily determined from package labeling in the United States, but more common in Europe and elsewhere. In some engineering fields, the British Thermal Unit (BTU), equal to about 1.055 kilo-joules, is widely used.
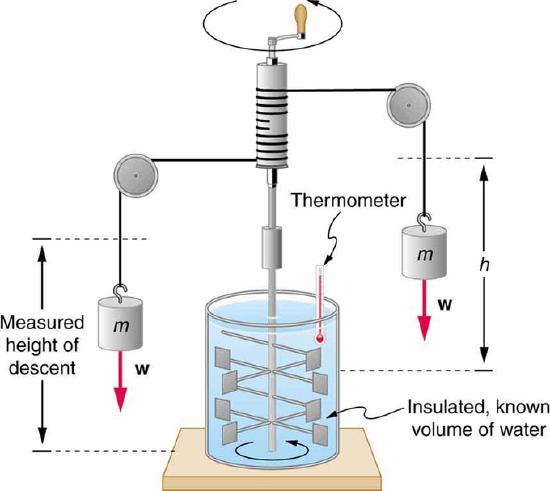
Figure 1 Equivalence of Heat and Work: Schematic depiction of Joule’s experiment that established the equivalence of heat and work
The total amount of energy transferred as heat is conventionally written as Q for algebraic purposes. Heat released by a system into its surroundings is by convention a negative quantity (Q < 0); when a system absorbs heat from its surroundings, it is positive (Q > 0).
Mechanical Equivalent of Heat
It is also possible to change the temperature of a substance by doing work. Work can transfer energy into or out of a system. This realization helped establish the fact that heat is a form of energy. James Prescott Joule (1818–1889) performed many experiments to establish the mechanical equivalent of heat—the work needed to produce the same effects as heat transfer. In terms of the units used for these two terms, the best modern value for this equivalence is 1.000 kcal = 4186 J. We consider this equation as the conversion between two different units of energy.
Figure 1 shows one of Joule’s most famous experimental setups for demonstrating the mechanical equivalent of heat. It demonstrated that work and heat can produce the same effects, and helped establish the principle of conservation of energy. Gravitational potential energy (PE) (work done by the gravitational force) is converted into kinetic energy (KE), and then randomized by viscosity and turbulence into increased average kinetic energy of atoms and molecules in the system, producing a temperature increase. His contributions to the field of thermodynamics were so significant that the SI unit of energy was named after him.
Heat added or removed from a system changes its internal energy (a concept we will discuss in the following section) and thus its temperature. Such a temperature increase is observed while cooking. However, adding heat does not necessarily increase the temperature. An example is melting of ice; that is, when a substance changes from one phase to another. Work done on the system or by the system can also change the internal energy of the system. Joule demonstrated that the temperature of a system can be increased by stirring. If an ice cube is rubbed against a rough surface, work is done by the frictional force. A system has a well-defined internal energy, but we cannot say that it has a certain “heat content” or “work content.” We use the phrase “heat transfer” to emphasize its nature.
Internal Energy
The internal energy of a system is the sum of all kinetic and potential energy in a system.
learning objectives
- Express the internal energy in terms of kinetic and potential energy
Internal Energy
James Joule showed that both heat and work can produce the same change in the internal energy of a substance, establishing the principle of the mechanical equivalence of heat. Heat is emphatically a quantity that solely describes energy being transferred. It makes no sense to speak of the total ‘heat’ an object or system contains. However, a system does contain a quantifiable amount of energy called the internal energy of a system. The internal energy of a system is the quantity that changes with the addition or subtraction of work or heat. It is closely related to temperature.
Definition
The internal energy is the energy required to create a system, excluding the energy necessary to displace its surroundings. Internal energy has two components: kinetic energy and potential energy. The kinetic energy consists of all the energy involving the motions of the particles constituting the system, including translation, vibration, and rotation. The potential energy is associated with the static constituents of matter, static electric energy of atoms within molecules or crystals, and the energy from chemical bonds. The equation describing the total internal energy of a system is then:
U=Ukinetic+Upotential.
We can also think of the internal energy as the sum of all the energy states of each component in the system:
U=∑iEi.
At any finite temperature, kinetic and potential energies are constantly converted into each other, but the total energy remains constant in an isolated system. The kinetic energy portion of internal energy gives rise to the temperature of the system. We can use statistical mechanics to relate the (somewhat) random motions of particles in a system to the mean kinetic energy of the ensemble of particles, and thus the empirically measurable quantity expressed as temperature.
We can see that internal energy is an extensive property: it depends on the size of the system or on the amount of substance it contains.
In most cases, we are not concerned with the total amount of internal energy in the system, as it is rarely convenient or necessary to consider all energies belonging to the system. Rather, we are far more interested in the change in internal energy, given some transfer of work or heat. This can be expressed as:
ΔU=Q+Wmech+Wother.
Q is heat added to a system and Wmech is the mechanical work performed by the surroundings due to pressure or volume changes in the system. All other perturbations and energies added by other processes, such as an electric current introduced into an electronic circuit, is summarized as the term Wextra.
We can calculate a small change in internal energy of the system by considering the infinitesimal amount of heat δQ added to the system minus the infinitesimal amount of work δW done by the system:
dU=δQ−δW.
This expression is the first law of thermodynamics.

The Sun and Internal Energy: Nuclear fusion in the sun converts nuclear potential energy into available internal energy and keeps the temperature of the Sun very high.
Key Points
- Heat is a crucial concept that touches every aspect of our lives. James Clerk Maxwell set down important principles that couple into the definition of heat.
- The quantity of heat transfer can be directly measured or estimated indirectly through the science of calorimetry.
- There are three modes of heat transfer: conduction, convection, and radiation.
- If two objects at different temperature are brought together, energy will transfer from the hotter object to the cooler one until both are at the same temperature. This transfer of energy is known as heat.
- Heat should not be confused with temperature. Temperature describes the internal state of an object, while heat refers to the energy transferred to or from the object.
- Since heat is a form of energy, its SI unit is the joule. Other common units of heat energy include the calorie and kilocalorie, equal to 4.186 and 4,186 joules, respectively.
- Because heat and work both involve the transfer of energy, they can each produce the same effects. The concept of the mechanical equivalent of heat was instrumental in establishing the principle of conservation of energy.
- While a system does not contain ‘ heat,’ it does contain a total amount of energy called internal energy.
- The internal energy is the energy necessary to create a system, minus the energy necessary to displace its surroundings.
- Most of the time, we are interested in the change in internal energy rather than the total internal energy.
- The first law of thermodynamics, dU=ΔQ−ΔW, describes small changes in internal energy.
Key Terms
- heat transfer: The transmission of thermal energy via conduction, convection, or radiation.
- calorimetry: The science of measuring the heat absorbed or evolved during the course of a chemical reaction or change of state.
- kilocalorie: A non-SI unit of energy equal to 1,000 calories or 4,186 joules; equal to the “calorie” or “Calorie” used in nutritional labeling. Symbol: kcal.
- thermal equilibrium: Two systems are in thermal equilibrium if they could transfer heat between each other, but don’t.
- mechanical equivalent of heat: The work needed to produce the same effects as heat transfer.
- internal energy: The sum of all energy present in the system, including kinetic and potential energy; equivalently, the energy needed to create a system, excluding the energy necessary to displace its surroundings.
- isolated system: A system that does not interact with its surroundings, that is, its total energy and mass stay constant.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42226/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42226/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42221/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42223/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Heat. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Heat. License: CC BY-SA: Attribution-ShareAlike
- calorimetry. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/calorimetry. License: CC BY-SA: Attribution-ShareAlike
- heat transfer. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/heat_transfer. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. October 15, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42221/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42223/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Heat. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Heat. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/thermal-equilibrium--2. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/mechanical-equivalent-of-heat. License: CC BY-SA: Attribution-ShareAlike
- kilocalorie. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/kilocalorie. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. October 15, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42221/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Heat Transfer. Located at: http://www.youtube.com/watch?v=pEBwctL490M. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, College Physics. October 13, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42223/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. October 13, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42223/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Internal energy. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/Internal_energy. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/internal-energy. License: CC BY-SA: Attribution-ShareAlike
- isolated system. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/isolated_system. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. October 15, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42221/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Heat Transfer. Located at: http://www.youtube.com/watch?v=pEBwctL490M. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, College Physics. October 13, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42223/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. October 13, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42223/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Heat. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Heat. License: Public Domain: No Known Copyright


