6.12: Non-Uniform Circular Motion
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 17919

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Overview of Non-Uniform Circular Motion
Non-uniform circular motion denotes a change in the speed of a particle moving along a circular path.
learning objectives
- Explain when a particle undergoes non-uniform circular motion
What do we mean by non-uniform circular motion? The answer lies in the definition of uniform circular motion, which is a circular motion with constant speed. It follows then that non-uniform circular motion denotes a change in the speed of the particle moving along the circular path. Note especially the change in the velocity vector sizes, denoting change in the magnitude of velocity.
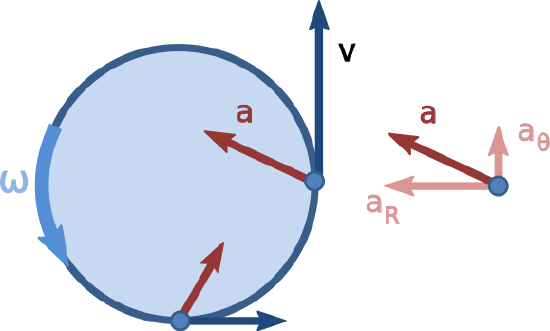
Diagram of non-uniform circular motion: In non-uniform circular motion, the magnitude of the angular velocity changes over time.
The change in direction is accounted by radial acceleration ( centripetal acceleration ), which is given by following relation: ar=v2r. The change in speed has implications for radial (centripetal) acceleration. There are two possibilities:
1: The radius of circle is constant (like in the motion along a circular rail or motor track). A change in v will change the magnitude of radial acceleration. This means that the centripetal acceleration is not constant, as is the case with uniform circular motion. The greater the speed, the greater the radial acceleration. A particle moving at higher speed will need a greater radial force to change direction and vice-versa when the radius of the circular path is constant.
2: The radial (centripetal) force is constant (like a satellite rotating about the earth under the influence of a constant force of gravity). The circular motion adjusts its radius in response to changes in speed. This means that the radius of the circular path is variable, unlike the case of uniform circular motion. In any eventuality, the equation of centripetal acceleration in terms of “speed” and “radius” must be satisfied. The important thing to note here is that, although change in speed of the particle affects radial acceleration, the change in speed is not affected by radial or centripetal force. We need a tangential force to affect the change in the magnitude of a tangential velocity. The corresponding acceleration is called tangential acceleration.
In either case, the angular velocity in non-uniform circular motion is not constant as ω=vr and v is varying.
Key Points
- In non- uniform circular motion, the size of the velocity vector (speed) changes, denoting change in the magnitude of velocity.
- The change in speed has implications for radial ( centripetal ) acceleration. There are two possibilities: 1) the radius of the circle is constant; or 2) the radial (centripetal) force is constant.
- In either case, the angular velocity in non-uniform circular motion is not constant, as ω=vr, and v varies.
Key Terms
- radial: Moving along a radius.
- centripetal: Directed or moving towards a center.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Non-uniform circular motion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Non-uniform_circular_motion. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Non-Uniform Circular Motion. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14020/latest/. License: CC BY: Attribution
- Non-uniform circular motion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Non-uniform_circular_motion. License: CC BY-SA: Attribution-ShareAlike
- centripetal. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/centripetal. License: CC BY-SA: Attribution-ShareAlike
- radial. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/radial. License: CC BY-SA: Attribution-ShareAlike
- File:Nonuniform circular motion.svg - Wikipedia, the free encyclopedia. Provided by: Wikipedia. Located at: en.Wikipedia.org/w/index.php?title=File:Nonuniform_circular_motion.svg&page=1. License: CC BY-SA: Attribution-ShareAlike

