6.16: Kepler’s Laws
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 17923

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Kepler’s First Law
Kepler’s first law is: The orbit of every planet is an ellipse with the Sun at one of the two foci.
learning objectives
- Apply Kepler’s first law to describe planetary motion
Kepler’s First Law
Kepler’s first law states that
Definition
The orbit of every planet is an ellipse with the Sun at one of the two foci.
An ellipse is a closed plane curve that resembles a stretched out circle. Note that the Sun is not at the center of the ellipse, but at one of its foci. The other focal point, f2, has no physical significance for the orbit. The center of an ellipse is the midpoint of the line segment joining its focal points. A circle is a special case of an ellipse where both focal points coincide.
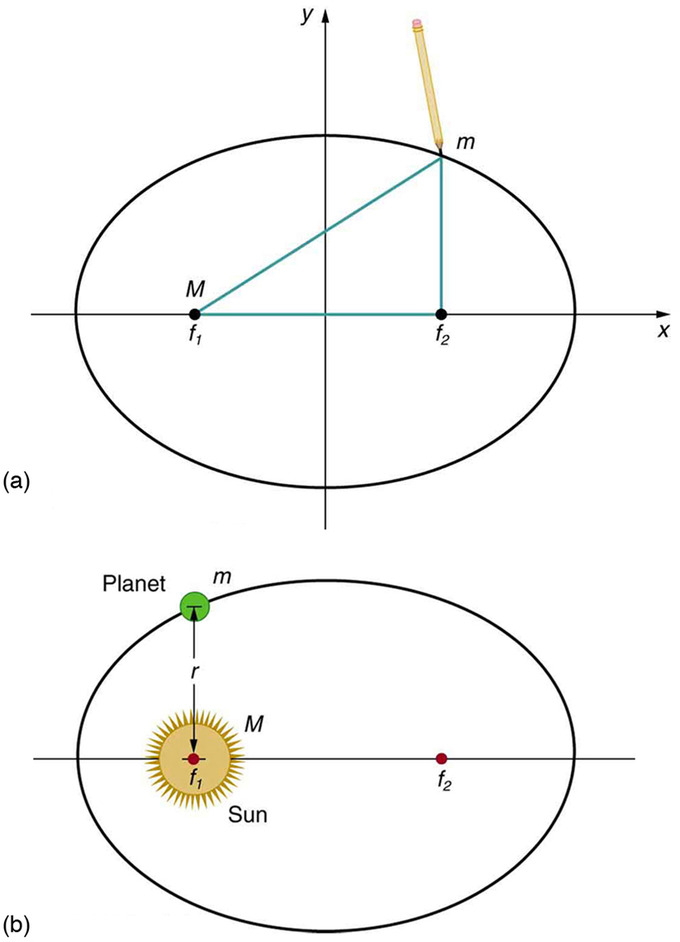
Ellipses and Kepler’s First Law: (a) An ellipse is a closed curve such that the sum of the distances from a point on the curve to the two foci (f1 and f2) is a constant. You can draw an ellipse as shown by putting a pin at each focus, and then placing a string around a pencil and the pins and tracing a line on paper. A circle is a special case of an ellipse in which the two foci coincide (thus any point on the circle is the same distance from the center). (b) For any closed gravitational orbit, m follows an elliptical path with M at one focus. Kepler’s first law states this fact for planets orbiting the Sun.
How stretched out an ellipse is from a perfect circle is known as its eccentricity: a parameter that can take any value greater than or equal to 0 (a circle) and less than 1 (as the eccentricity tends to 1, the ellipse tends to a parabola). The eccentricities of the planets known to Kepler varied from 0.007 (Venus) to 0.2 (Mercury). Minor bodies such as comets an asteroids (discovered after Kepler’s time) can have very large eccentricities. The dwarf planet Pluto, discovered in 1929, has an eccentricity of 0.25.
Symbolically, an ellipse can be represented in polar coordinates as:
\mathrm{r=\dfrac{p}{1+ϵ \cos θ}}
where \mathrm{(r,θ)} are the polar coordinates (from the focus) for the ellipse, \mathrm{p} is the semi-latus rectum, and \mathrm{ϵ} is the eccentricity of the ellipse. For a planet orbiting the Sun, \mathrm{r} is the distance from the Sun to the planet and \mathrm{θ} is the angle between the planet’s current position and its closest approach, with the Sun as the vertex.
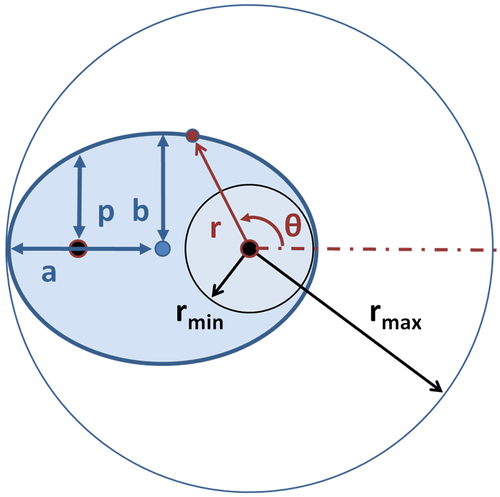
Orbit As Ellipse: Heliocentric coordinate system \mathrm{(r,θ)} for ellipse. Also shown are: semi-major axis \mathrm{a}, semi-minor axis \mathrm{b} and semi-latus rectum \mathrm{p}; center of ellipse and its two foci marked by large dots. For \mathrm{θ=0°}, \mathrm{r=r_{min}} and for \mathrm{θ=180°}, \mathrm{r=r_{max}}.
At \mathrm{θ=0°}, perihelion, the distance is minimum
\mathrm{r_{min}=\dfrac{p}{1+ϵ}.}
At \mathrm{θ=90°} and at \mathrm{θ=270°}, the distance is \mathrm{p}.
At \mathrm{θ=180°}, aphelion, the distance is maximum
\mathrm{r_{max}=\dfrac{p}{1−ϵ}.}
The semi-major axis \mathrm{a} is the arithmetic mean between \mathrm{r_{min}} and \mathrm{r_{max}}:
\mathrm{r_{max}−a=a−r_{min}}
\mathrm{a=\dfrac{p}{1−ϵ^2}.}
The semi-minor axis \mathrm{b} is the geometric mean between \mathrm{r_{min}} and \mathrm{r_{max}}:
\mathrm{\dfrac{r_{max}}{b}=\dfrac{b}{r_{min}}}
\mathrm{b=\dfrac{p}{\sqrt{1−ϵ^2}}}
The semi-latus rectum \mathrm{p} is the harmonic mean between \mathrm{r_{min}} and \mathrm{r_{max}}:
\mathrm{\dfrac{1}{r_{min}}−\dfrac{1}{p}=\dfrac{1}{p}−\dfrac{1}{r_{max}}}
\mathrm{pa=r_{max}⋅r_{min}=b^2.}
The eccentricity \mathrm{ϵ} is the coefficient of variation between \mathrm{r_{min}} and \mathrm{r_{max}} :
\mathrm{ϵ=\dfrac{r_{max}−r_{min}}{r_{max}+r_{min}}}
The area of the ellipse is
\mathrm{A=πab}
The special case of a circle is \mathrm{ϵ=0}, resulting in \mathrm{r=p=r_{min}=r_{max}=a=b} and \mathrm{A=πr^2}. The orbits of planets with very small eccentricities can be approximated as circles.
Understanding Kepler’s 3 Laws and Orbits: In this video you will be introduced to Kepler’s 3 laws and see how they are relevant to orbiting objects.
Kepler’s Second Law
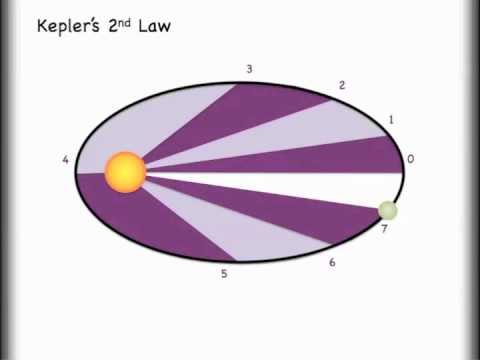
Kepler’s second law states: A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
learning objectives
- Apply Kepler’s second law to describe planetary motion
Kepler’s second law states:
Definition
A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
Understanding Kepler’s 3 Laws and Orbits: In this video you will be introduced to Kepler’s 3 laws and see how they are relevant to orbiting objects.
In a small time the planet sweeps out a small triangle having base line and height. The area of this triangle is given by:
\mathrm{dA=\frac{1}{2}⋅r⋅rdθ}
and so the constant areal velocity is:
\mathrm{\dfrac{dA}{dt}=\dfrac{1}{2}r^2\dfrac{dθ}{dt}}
Now as the first law states that the planet follows an ellipse, the planet is at different distances from the Sun at different parts in its orbit. So the planet has to move faster when it is closer to the Sun so that it sweeps equal areas in equal times.
The total area enclosed by the elliptical orbit is:
\mathrm{A=πab}
Therefore the period \mathrm{P} satisfies:
\mathrm{πab=P⋅\dfrac{1}{2}r^2 \dot{θ} \text{ or } r^2 \dot{θ}=nab}
Where \mathrm{\dot{θ}=\frac{dθ}{dt}} is the angular velocity, (using Newton notation for differentiation), and \mathrm{n=\frac{2π}{P}} is the mean motion of the planet around the Sun.
See below for an illustration of this effect. The planet traverses the distance between A and B, C and D, and E and F in equal times. When the planet is close to the Sun it has a larger velocity, making the base of the triangle larger, but the height of the triangle smaller, than when the planet is far from the Sun. One can see that the planet will travel fastest at perihelion and slowest at aphelion.
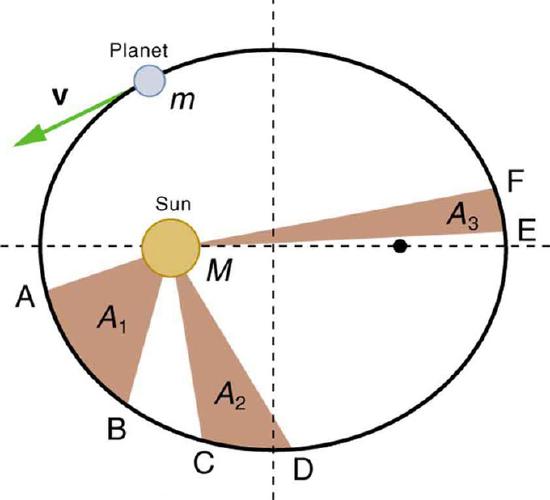
Kepler’s Second Law: The shaded regions have equal areas. It takes equal times for m to go from A to B, from C to D, and from E to F. The mass m moves fastest when it is closest to M. Kepler’s second law was originally devised for planets orbiting the Sun, but it has broader validity.
Kepler’s Third Law
Kepler’s third law states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
learning objectives
- Apply Kepler’s third law to describe planetary motion
Kepler’s Third Law
Kepler’s third law states:
Definition
The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
The third law, published by Kepler in 1619, captures the relationship between the distance of planets from the Sun, and their orbital periods. Symbolically, the law can be expressed as
\mathrm{P^2∝a^3,}
where P is the orbital period of the planet and a is the semi-major axis of the orbit (see ).
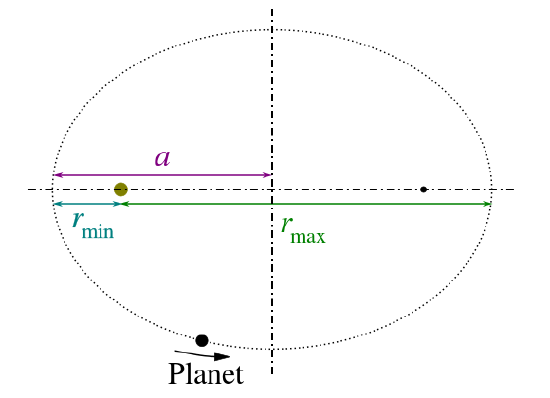
Kepler’s Third Law: Kepler’s third law states that the square of the period of the orbit of a planet about the Sun is proportional to the cube of the semi-major axis of the orbit.
The constant of proportionality is
\mathrm{\dfrac{P_{planet}^2}{a_{planet}^3}=\dfrac{P_{earth}^2}{a_{earth}^3}=1\dfrac{yr^2}{AU^3}}
for a sidereal year (yr), and astronomical unit (AU).
Kepler enunciated this third law in a laborious attempt to determine what he viewed as the “music of the spheres” according to precise laws, and express it in terms of musical notation. Therefore, it used to be known as the harmonic law.
Derivation of Kepler’s Third Law
We can derive Kepler’s third law by starting with Newton’s laws of motion and the universal law of gravitation. We can therefore demonstrate that the force of gravity is the cause of Kepler’s laws.
Consider a circular orbit of a small mass m around a large mass M. Gravity supplies the centripetal force to mass m. Starting with Newton’s second law applied to circular motion,
\mathrm{F_{net}=ma_c=m\dfrac{v^2}{r}.}
The net external force on mass m is gravity, and so we substitute the force of gravity for Fnet:
\mathrm{G\dfrac{mM}{r^2}=m\dfrac{v^2}{r}}
The mass m cancels, as well as an r, yielding
\mathrm{G\dfrac{M}{r}=v^2}
The fact that m cancels out is another aspect of the oft-noted fact that at a given location all masses fall with the same acceleration. Here we see that at a given orbital radius r, all masses orbit at the same speed. This was implied by the result of the preceding worked example. Now, to get at Kepler’s third law, we must get the period P into the equation. By definition, period P is the time for one complete orbit. Now the average speed v is the circumference divided by the period—that is,
\mathrm{v=\dfrac{2πr}{P}.}
Substituting this into the previous equation gives
\mathrm{G\dfrac{M}{r}=\dfrac{4π^2r^2}{P^2}}
Solving for P2 yields
\mathrm{P^2=\dfrac{4π^2r^3}{GM}.}
Using subscripts 1 and 2 to denote two different satellites, and taking the ratio of the last equation for satellite 1 to satellite 2 yields
\mathrm{\dfrac{P^2_1}{P^2_2}=\dfrac{r^3_1}{r^3_2}}
This is Kepler’s third law. Note that Kepler’s third law is valid only for comparing satellites of the same parent body, because only then does the mass of the parent body M cancel.
Now consider what one would get when solving \mathrm{P^2=\frac{4π^2GM}{r^3}} for the ratio \mathrm{\frac{r^3}{P^2}}. We obtain a relationship that can be used to determine the mass M of a parent body from the orbits of its satellites:
\mathrm{M=\dfrac{4π^2r^3}{GP^2}}
If r and P are known for a satellite, then the mass M of the parent can be calculated. This principle has been used extensively to find the masses of heavenly bodies that have satellites. Furthermore, the ratio \mathrm{\frac{r^3}{T^2}} should be a constant for all satellites of the same parent body (because \mathrm{\frac{r^3}{T^2}=\frac{GM}{4π^2}}).
Understanding Kepler’s 3 Laws and Orbits: In this video you will be introduced to Kepler’s 3 laws and see how they are relevant to orbiting objects.
Orbital Maneuvers
An orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft (the rest of the flight is called “coasting”).
learning objectives
- Explain purpose of an orbital maneuver
Orbital Maneuvers
In spaceflight, an orbital maneuver is the use of propulsion systems to change the orbit of a spacecraft. The rest of the flight, especially in a transfer orbit, is called coasting.
Rocket Equation
The Tsiolkovsky rocket equation or ideal rocket equation is an equation useful for considering vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself (a thrust) by expelling part of its mass with high speed and moving due to the conservation of momentum. Specifically, it is a mathematical equation relating the delta-v with the effective exhaust velocity and both the initial and final mass of a rocket (or other reaction engine).
For any such maneuver (or journey involving a number of such maneuvers):
\mathrm{Δv=v_e \ln (\dfrac{m_0}{m_1}),}
where:
- m0 is the initial total mass, including propellant;
- m1 is the final total mass;
- ve is the effective exhaust velocity (ve=Isp • g0 where Isp is the specific impulse expressed as a time period and g0 is the gravitational constant); and
- Δv is delta-v the maximum change of speed of the vehicle (with no external forces acting).
See for an illustration plotting the relationship between final velocity and rocket mass ratios (according to the rocket equation).
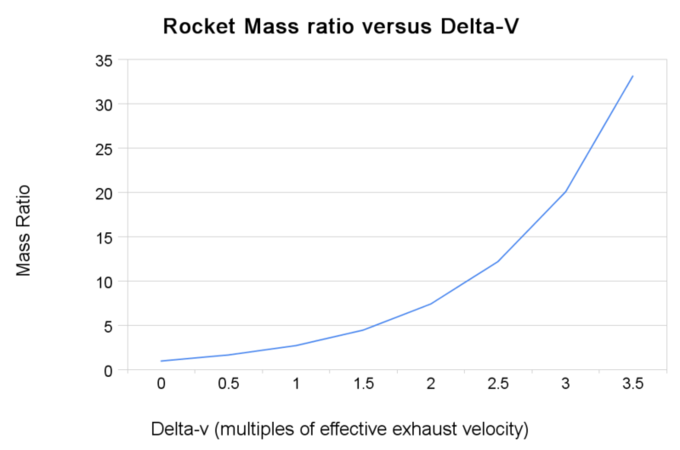
Rocket Equation: Rocket mass ratios versus final velocity calculated from the rocket equation
Delta-v Budget:
The total delta-v for each maneuver estimated for a mission is called a delta-v budget. With a good approximation of the delta-v budget, designers can estimate the fuel to payload requirements of the spacecraft using the rocket equation.
Oberth Effect and Gravitational Assist
In astronautics, the Oberth effect occurs when the use of a rocket engine travelling at high speed generates much more useful energy than one at low speed. This effect is the result of propellant having more usable energy (due to its kinetic energy on top of its chemical potential energy). The vehicle is able to employ this kinetic energy to generate more mechanical power.
Oberth effect is used in a powered flyby or Oberth maneuver in which the application of an impulse (typically from the use of a rocket engine) close to a gravitational body (where the gravity potential is low and the speed is high) allows for more change in kinetic energy and final speed (i.e. higher specific energy) than the same impulse applied further from the body for the same initial orbit.
In orbital mechanics, a gravitational slingshot (or gravity assist maneuver) is the use of the relative movement and gravity of a planet or other celestial body to alter the path and speed of a spacecraft, typically in an effort to save propellant, time, and expense. Gravity assistance can be used to accelerate, decelerate and/or re-direct the path of a spacecraft. This technique was used by the Voyager probes in their fly-bys of Jupiter and Saturn (see ).
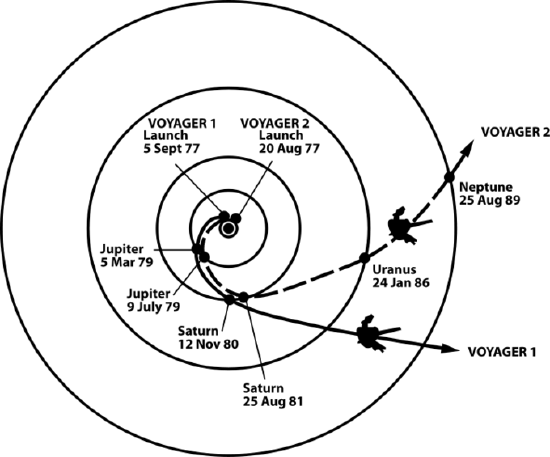
Voyager Path Using Gravity Assists: The trajectories that enabled NASA’s twin Voyager spacecraft to tour the four gas giant planets and achieve velocity to escape our solar system
Transfer Orbits
Orbit insertion is a general term used for a maneuver when it is more than a small correction. It may be used in a maneuver to change a transfer orbit or an ascent orbit into a stable one, but also to change a stable orbit into a descent (i.e., descent orbit insertion). Also, the term orbit injection is used, especially for changing a stable orbit into a transfer orbit—e.g., trans-lunar injection (TLI), trans-Mars injection (TMI) and trans-Earth injection (TEI).
The Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different altitudes in the same plane. The orbital maneuver to perform the Hohmann transfer uses two engine impulses that move aspacecraft onto and off the transfer orbit, as diagramed in. Hohmann transfer orbits are the most efficient with fuel. Other non-Hohmann types of transfer orbits that are less efficient with fuel exist, but these may be more efficient with other resources (such as time).
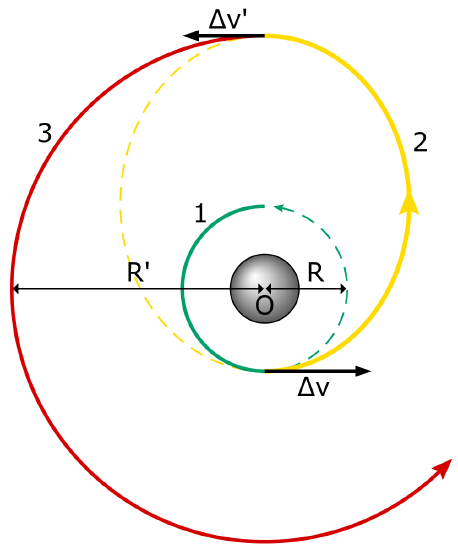
Hohmann Transfer Orbit: A diagram of the Hohmann Transfer Orbit.
Orbital inclination change is an orbital maneuver aimed at changing an orbiting body’s orbit inclination (this maneuver is also known as an orbital plane change as the plane of the orbit is tipped). The maneuver requires a change in the orbital velocity vector (delta-v) at the orbital nodes (i.e., the point at which the initial and desired orbits intersect: the line of orbital nodes is defined by the intersection of the two orbital planes).
Satellites
Natural satellites are celestial objects that orbit a larger body; artificial satellites are manmade objects put in the orbit of the Earth.
learning objectives
- Define the concept of a satellite, in the broadest possible terms
Satellites
The word “satellite” has a somewhat ambiguous definition. The broadest possible definition of a satellite is an object that orbits a larger one due to the force of gravity. Natural satellites, often called moons (see ), are celestial bodies that orbit a larger body call a primary (often planet, though there are binary asteroids, too). It is technically correct to refer to a planet as a “satellite” of its parent star, though this is not common.

Moons of the Solar System: Nineteen natural satellites are large enough to be round, and one, Saturn’s Titan, has a substantial atmosphere.
Artificial satellites (see ) are man made objects put in orbit about the Earth or another planet in the Solar System. All satellites follow the laws of orbital mechanics, which can almost always be approximated with Newtonian physics.

Orbital Altitudes: Orbital Altitudes of several significant satellites of earth.
Natural satellites are often classified in terms of their size and composition, while artificial satellites are categorized in terms of their orbital parameters.
Natural Satellites
Formally classified natural satellites, or moons, include 176 planetary satellites orbiting six of the eight planets, and eight orbiting three of the five IAU-listed dwarf planets. As of January 2012, over 200 minor-planet moons have been discovered. There are 76 objects in the asteroid belt with satellites (five with two satellites each), four Jupiter trojans, 39 near-Earth objects, and 14 Mars-crossers. There are also 84 known natural satellites of trans-Neptunian objects. Planets around other stars are likely to have natural satellites as well, although none have yet been observed.
Of the inner planets, Mercury and Venus have no natural satellites; Earth has one large natural satellite, known as the Moon; and Mars has two tiny natural satellites, Phobos and Deimos. The large gas giants have extensive systems of natural satellites, including half a dozen comparable in size to Earth’s Moon: the four Galilean moons, Saturn’s Titan, and Neptune’s Triton. Saturn has an additional six mid-sized natural satellites massive enough to have achieved hydrostatic equilibrium, and Uranus has five. It has been suggested that some satellites may potentially harbor life, though there is currently no direct evidence.
The Earth–Moon system is unique in that the ratio of the mass of the Moon to the mass of the Earth is much greater than that of any other natural satellite to planet ratio in the Solar System. Additionally the Moon’s orbit with respect to the Sun is always concave.
The seven largest natural satellites in the Solar System (those bigger than 2,500 km across) are Jupiter’s Galilean moons (Ganymede, Callisto, Io, and Europa), Saturn’s moon Titan, Earth’s moon, and Neptune’s captured natural satellite Triton.
Artificial Satellites
The first satellite, Sputnik 1, was put into orbit around Earth and was therefore in geocentric orbit. By far this is the most common type of orbit with about 2,500 artificial satellites orbiting the Earth. Geocentric orbits may be further classified by their altitude, inclination and eccentricity.
The commonly used altitude classifications are Low Earth orbit (LEO), Medium Earth orbit (MEO) and High Earth orbit (HEO). Low Earth orbit is any orbit below 2000 km, and Medium Earth orbit is any orbit higher than that but still below the altitude for geosynchronous orbit at 35,786 km. High Earth orbit is any orbit higher than the altitude for geosynchronous orbit.
Altitude classifications
- Low Earth orbit (LEO): Geocentric orbits ranging in altitude from 0–2000 km (0–1240 miles)
- Medium Earth orbit (MEO): Geocentric orbits ranging in altitude from 2,000 km (1,200 mi) to just below geosynchronous orbit at 35,786 km (22,236 mi). Also known as an intermediate circular orbit.
- High Earth orbit (HEO): Geocentric orbits above the altitude of geosynchronous orbit 35,786 km (22,236 mi).
Inclination Classifications
- Inclined orbit: An orbit whose inclination in reference to the equatorial plane is not zero degrees.
- Polar orbit: An orbit that passes above or nearly above both poles of the planet on each revolution. Therefore it has an inclination of (or very close to) 90 degrees.
- Polar sun synchronous orbit: A nearly polar orbit that passes the equator at the same local time on every pass. Useful for image taking satellites because shadows will be nearly the same on every pass.
Eccentricity Classifications
- Circular orbit: An orbit that has an eccentricity of 0 and whose path traces a circle.
- Hohmann transfer orbit: An orbital maneuver that moves a spacecraft from one circular orbit to another using two engine impulses.
- Elliptic orbit: An orbit with an eccentricity greater than 0 and less than 1 whose orbit traces the path of an ellipse.
- Geosynchronous transfer orbit: An elliptic orbit where the perigee is at the altitude of a Low Earth orbit (LEO) and the apogee at the altitude of a geosynchronous orbit.
- Geostationary transfer orbit: An elliptic orbit where the perigee is at the altitude of a Low Earth orbit (LEO) and the apogee at the altitude of a geostationary orbit.
Key Points
- An ellipse is a closed plane curve that resembles a stretched out circle (The Sun is at one focus while the other focus has no physical significance. A circle is a special case of an ellipse where both focal points coincide.
- How stretched out an ellipse is from a perfect circle is known as its eccentricity: a parameter that can take any value greater than or equal to 0 (a circle) and less than 1 (as the eccentricity tends to 1, the ellipse tends to a parabola).
- Symbolically, an ellipse can be represented in polar coordinates as: \mathrm{r=\frac{p}{1+ϵ \cos θ}}, where \mathrm{(r,θ)} are the polar coordinates (from the focus) for the ellipse, \mathrm{p} is the semi-latus rectum, and \mathrm{ϵ} is the eccentricity of the ellipse.
- Perihelion is minimum distance from the Sun a planet achieves in its orbit and is given by\mathrm{r_{max}=\frac{p}{1−ϵ}.} Aphelion is the largest distance from the Sun a planet reaches in his orbit and is given by \mathrm{r_{max}=\dfrac{p}{1−ϵ}.}
- In a small time the planet sweeps out a small triangle having base line and height. The area of this triangle is given by \mathrm{dA=\frac{1}{2}⋅r⋅rdθ} and so the constant areal velocity is: \mathrm{\frac{dA}{dt}=\dfrac{1}{2}r^2\dfrac{dθ}{dt}}
- The period \mathrm{P} satisfies: \mathrm{πab=P⋅\frac{1}{2}r^2 \dot{θ}}. One can see that the product of \mathrm{r^2} and must be constant, so that when the planet is further from the Sun it travels at a slower rate and vise versa.
- A planet travels fastest at perihelion and slowest at aphelion.
- Kepler’s third law can be represented symbolically as \mathrm{P^2∝a^3,} where P is the orbital period of the planet and a is the semi-major axis of the orbit (see.
- The constant of proportionality is \mathrm{\dfrac{P_{planet}^2}{a_{planet}^3}=\frac{P_{earth}^2}{a_{earth}^3}=1\frac{yr^2}{AU^3}} for a sidereal year (yr), and astronomical unit (AU).
- Kepler’s third law can be derived from Newton’s laws of motion and the universal law of gravitation. Set the force of gravity equal to the centripetal force. After substituting an expression for the velocity of the planet, one can obtain: \mathrm{G\frac{M}{r}=\frac{4πr^2}{P^2}} which can also be written \mathrm{P^2=\frac{4π^2a^3}{GM}.}
- Using the expression above we can obtain the mass of the parent body from the orbits of its satellites: \mathrm{M=\frac{4π^2r^3}{GP^2}}
- The ideal rocket equation related the maximum change in velocity attainable by a rocket ( delta-v or Δv) as a function of the exhaust velocity (ve) and the ratio between the mass of the rocket with and without the propellant (m0/m1). The equation is given by \mathrm{Δv=v_e \ln (\dfrac{m_0}{m_1})}.
- The Oberth effect: where the use of a rocket engine travelling at high speed generates more useful energy than one at low speed. Thus it is more efficient to apply thrust when the spacecraft is nearest to the planet (periastron).
- A gravity assist maneuver is the use of the relative movement and gravity of a planet (or other celestial body) to alter the velocity of a spacecraft—typically in order to save propellant, time, and expense. This technique was employed by the Voyager probes (see.
- The Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different altitudes, in the same plane. The orbital maneuver to perform the Hohmann transfer uses two engine impulses which move aspacecraft onto and off the transfer orbit. See.
- The broadest possible definition of a satellite is an object that orbits a larger one due to the force of gravity.
- All satellites follow the laws of orbital mechanics, which can almost always be approximated with Newtonian physics.
- Natural satellites are often classified in terms of their size and composition, while artificial satellites are categorized in terms of their orbital parameters.
- Artificial Earth-orbiting satellites have orbits categorized by their altitudes, inclinations, and eccentricities.
Key Terms
- eccentricity: The coefficient of variation between \mathrm{r_{min}} and \mathrm{r_{max}}: \mathrm{ϵ=\dfrac{r_{max}−r_{min}}{r_{max}+r_{min}}} The further appart the foci are, the stronger the eccentricity.
- perihelion: The point in the elliptical orbit of a planet or comet etc. where it is nearest to the Sun. The point farthest from the Sun is called aphelion.
- semi-latus rectum: The latus rectum is a chord perpendicular to the major axis and passing through the focus. The semi-latus rectum is half the latus rectrum. See distance p in.
- angular velocity: A vector quantity describing an object in circular motion; its magnitude is equal to the speed of the particle and the direction is perpendicular to the plane of its circular motion.
- mean motion: An angle of \mathrm{2π} (radians) divided by the orbital period (of a celestial body in an elliptic orbit).
- astronomical unit: The mean distance from the Earth to the Sun (the semi-major axis of Earth’s orbit), approximately 149,600,000 kilometres (symbol AU), used to measure distances in the solar system.
- sidereal year: The orbital period of the Earth; a measure of the time it takes for the Sun to return to the same position with respect to the stars of the celestial sphere. A sidereal year is about 20.4 minutes longer than the tropical year due to precession of the equinoxes.
- Hohmann transfer orbit: The Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different altitudes, in the same plane. The orbital maneuver to perform the Hohmann transfer uses two engine impulses, one to move a spacecraft onto the transfer orbit and a second to move off it.
- delta-v: The maximum change in the scalar speed of a rocket if the rocket were operated in a vacuum away from external forces (i.e., if no other external forces act).
- natural satellite: A natural satellite, moon, or secondary planet is a celestial body that orbits a planet or smaller body, which is called its primary.
- artificial satellite: In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike