5.12: Multiple Velocities
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18146

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Addition of Velocities
Relative velocities can be found by adding the velocity of the observed object to the velocity of the frame of reference it was measured in.
As learned in a previous atom, relative velocity is the velocity of an object as observed from a certain frame of reference.
demonstrates the concept of relative velocity. The girl is riding in a sled at 1.0 m/s, relative to an observer. When she throws the snowball forward at a speed of 1.5 m/s, relative to the sled, the velocity of the snowball to the observer is the sum of the velocity of the sled and the velocity of the snowball relative to the sled:
\mathrm{1.0 m/s+1.5 m/s=2.5 m/s}
If the girl were to throw the snowball behind her at the same speed, the velocity of the ball relative to the observer would be:
\mathrm{1.0 m/s−1.5 m/s=−0.5 m/s}
The concept of relative velocity can also be demonstrated using the example of a boat in a river with a current. The boat is only trying to move forward, but since the river is in motion, it carries the boat sideways while it moves forward. The person on the boat is only observing the forward motion, while an observer on the shore will notice that the boat is moving sideways. In order to calculate the velocity that the object is moving relative to earth, it is helpful to remember that velocity is a vector. In order to analytically add these vectors, you need to remember the relationship between the magnitude and direction of the vector and its components on the x and y axis of the coordinate system:
- Magnitude: \mathrm{v=\sqrt{v_x^2+v_y^2}}
- Direction: \mathrm{θ=tan^{−1}(\frac{v_y}{v_x})}
- x-component: \mathrm{v_x=v \cos θ}
- y-component: \mathrm{v_y=v \sin θ}
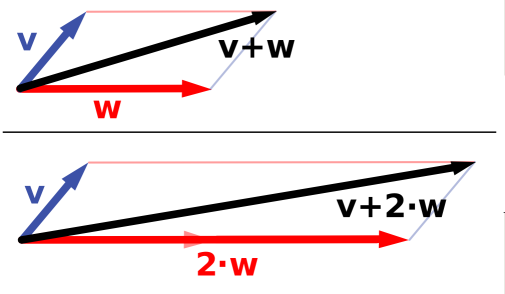
Vector Addition: Addition of velocities is simply the addition of vectors.
These components are shown above. The first two equations are for when the magnitude and direction are known, but you are looking for the components. The last two equations are for when the components are known, and you are looking for the magnitude and direction. The magnitude of the observed velocity from the shore is the square root sum of the squared velocity of the boat and the squared velocity of the river.
Relative Velocity
Relative velocity is the velocity of an object B measured with respect to the velocity of another object A, denoted as \mathrm{v_{BA}}.
Relative velocity is the velocity of an object B, in the rest frame of another object A. This is denoted as \mathrm{v_{AB}} , where A is the velocity in the rest frame of B.
Galileo observed the concept of relative velocity by using an example of a fly and a boat. He observed that while you are aboard the boat, if you see a fly, you can measure its velocity, \mathrm{u}. You can then go back on land and measure the velocity of the boat, \mathrm{v}. Is the velocity of the fly, \mathrm{u}, the actual velocity of the fly? No, because what you measured was the velocity of the fly relative to the velocity of the boat. To obtain the velocity of the fly relative to the shore, \mathrm{s}, you can use the vector sum as shown: \mathrm{s=u+v}
Examples of Relative Velocity
This concept is best explained using examples. Pretend you are sitting in a passenger train that is moving east. If you were to look out the window and see a man walking in the same direction, it would appear the the man is moving much slower than he actually is. Now imagine you are standing outside and observe the same man walking next to the train. It will appear the the man is walking much faster than it seemed when you were inside the train.
Now, imagine you are on a boat, and you see a man walking from one end of the deck to the other. The velocity that you observe the man walking in will be the same velocity that he would be walking in if you both were on land. Now imagine that you are on land and see the man on the moving boat, walking from one end of the deck to another. It will now appear that the man is walking much faster than it appeared when you were on the boat with him.
Why is this? The concept of relative velocity has to do with your frame of reference. When you were on the train, your frame of reference was moving in the same direction that the man was walking, so it appeared that he was walking slower. But once you were off the train, you were in a stationary frame of reference, so you were able to observe him moving at his actual speed. When you were on the boat, you were in a moving frame of reference, but so was the object you were observing, so you were able to observe the man walking at his actual velocity. Once you were back on land, you were in a stationary frame of reference, but the man was not, so the velocity you saw was his relative velocity.
Key Points
- In order to find the velocity of an object B that is moving on object A that is observed by an observer that is not moving, add the velocity of B and A together.
- Velocity is a vector quantity, so the relationships between the magnitude, direction, x- axis component and y-axis component are important.
- These vector components can be added analytically or graphically.
- In order to calculate the magnitude and direction, you must know the values of the axis components (either \mathrm{x} and \mathrm{y}, or \mathrm{x, y,} and \mathrm{z}) and to calculate the component values, you must know the magnitude and direction.
- Relative velocity is the velocity of an object in motion being observed from a frame of reference that is either also in motion or stationary.
- If the frame of reference is moving in the same direction as the object being observed, it will appear as though the object is moving slower than it actually is.
- If the object being observed is on a moving surface, the velocity observed from that surface will be less than the velocity observed from a stationary surface looking onto the moving surface.
- In Galileo’s example, the observed velocity of the fly, uu, measured in reference to the velocity of the boat, \mathrm{v}. In order to find the velocity of the fly with respect to the shore, S, he had to add the velocity of the boat to the observed velocity of the fly: \mathrm{s=u+v}.
Key Terms
- relative: Expressed in relation to another item, rather than in complete form.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Velocity-addition formula. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Velocity-addition_formula. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Addition of Velocities. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42045/latest/. License: CC BY: Attribution
- relative. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/relative. License: CC BY-SA: Attribution-ShareAlike
- Vector Addition and Scaling. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Vector_space. License: CC BY-SA: Attribution-ShareAlike
- Velocity-addition formula. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/Velocity-addition_formula. License: CC BY-SA: Attribution-ShareAlike
- Relative velocity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Relative_velocity. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Relative Velocity in Two Dimensions. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14030/latest/. License: CC BY: Attribution
- relative. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/relative. License: CC BY-SA: Attribution-ShareAlike
- Vector Addition and Scaling. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/Vector_space. License: CC BY-SA: Attribution-ShareAlike

