5.11: Projectile Motion Revisited
- Last updated
- Save as PDF
- Page ID
- 18145

- Boundless
- Boundless
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Basic Equations and Parabolic Path
Projectile motion is a form of motion where an object moves in parabolic path; the path that the object follows is called its trajectory.
learning objectives
- Assess the effect of angle and velocity on the trajectory of the projectile; derive maximum height using displacement
Projectile Motion
Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning on the trajectory, after which the only interference is from gravity. In a previous atom we discussed what the various components of an object in projectile motion are. In this atom we will discuss the basic equations that go along with them in the special case in which the projectile initial positions are null (i.e. \(\mathrm{x_0=0}\) and \(\mathrm{y_0=0}\) ).
Initial Velocity
The initial velocity can be expressed as x components and y components:
\[\begin{align} \mathrm{u_x} & \mathrm{=u⋅ \cos θ} \\ \mathrm{u_y} & \mathrm{=u⋅ \sin θ} \end{align}\]
In this equation, \(\mathrm{u}\) stands for initial velocity magnitude and \(θ\) refers to projectile angle.
Time of Flight
The time of flight of a projectile motion is the time from when the object is projected to the time it reaches the surface. As we discussed previously, \(\mathrm{T}\) depends on the initial velocity magnitude and the angle of the projectile:
\[\begin{align} \mathrm{T} & \mathrm{=\dfrac{2⋅u_y}{g} } \\ \mathrm{T} & \mathrm{=\dfrac{2⋅u⋅\sin θ}{g}} \end{align}\]
Acceleration
In projectile motion, there is no acceleration in the horizontal direction. The acceleration, \(\mathrm{a}\), in the vertical direction is just due to gravity, also known as free fall:
\[\begin{align} \mathrm{a_x} & \mathrm{=0} \\ \mathrm{a_y} &\mathrm{=−g} \end{align}\]
Velocity
The horizontal velocity remains constant, but the vertical velocity varies linearly, because the acceleration is constant. At any time, \(\mathrm{t}\), the velocity is:
\[\begin{align} \mathrm{u_x} & \mathrm{=u⋅ \cos θ} \\ \mathrm{u_y} & \mathrm{=u⋅ \sin θ−g⋅t} \end{align}\]
You can also use the Pythagorean Theorem to find velocity:
\[\mathrm{u=\sqrt{u_x^2+u_y^2}}\]
Displacement
At time, t, the displacement components are:
\[\begin{align} \mathrm{x} & \mathrm{=u⋅t⋅ \cos θ} \\ \mathrm{y} & \mathrm{=u⋅t⋅ \sin θ−\dfrac{1}{2}gt^2} \end{align}\]
The equation for the magnitude of the displacement is \(\mathrm{Δr=\sqrt{x^2+y^2}}\).
Parabolic Trajectory
We can use the displacement equations in the x and y direction to obtain an equation for the parabolic form of a projectile motion:
\[\mathrm{y=\tan θ⋅x−\dfrac{g}{2⋅u^2⋅ \cos ^2 θ}⋅x^2}\]
Maximum Height
The maximum height is reached when \(\mathrm{v_y=0}\). Using this we can rearrange the velocity equation to find the time it will take for the object to reach maximum height
\[\mathrm{t_h=\dfrac{u⋅\sin θ}{g}}\]
where \(\mathrm{t_h}\) stands for the time it takes to reach maximum height. From the displacement equation we can find the maximum height
\[\mathrm{h=\dfrac{u^2⋅ \sin ^2 θ}{2⋅g}}\]
Range
The range of the motion is fixed by the condition \(\mathrm{y=0}\). Using this we can rearrange the parabolic motion equation to find the range of the motion:
\[\mathrm{R=\dfrac{u^2⋅ \sin 2 θ}{g}.}\]
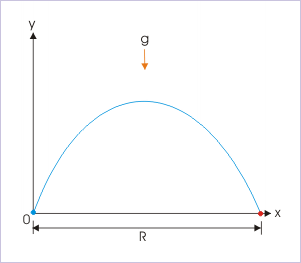
Range of Trajectory: The range of a trajectory is shown in this figure.
Projectiles at an Angle: This video gives a clear and simple explanation of how to solve a problem on Projectiles Launched at an Angle. I try to go step by step through this difficult problem to layout how to solve it in a super clear way. 2D kinematic problems take time to solve, take notes on the order of how I solved it. Best wishes. Tune into my other videos for more help. Peace.
Solving Problems
In projectile motion, an object moves in parabolic path; the path the object follows is called its trajectory.
learning objectives
- Identify which components are essential in determining projectile motion of an object
We have previously discussed projectile motion and its key components and basic equations. Using that information, we can solve many problems involving projectile motion. Before we do this, let’s review some of the key factors that will go into this problem-solving.
What is Projectile Motion?
Projectile motion is when an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning, after which the only influence on the trajectory is that of gravity.
What are the Key Components of Projectile Motion?
The key components that we need to remember in order to solve projectile motion problems are:
- Initial launch angle, \(\mathrm{θ}\)
- Initial velocity, \(\mathrm{u}\)
- Time of flight, \(\mathrm{T}\)
- Acceleration, \(\mathrm{a}\)
- Horizontal velocity, \(\mathrm{v_x}\)
- Vertical velocity, \(\mathrm{v_y}\)
- Displacement, \(\mathrm{d}\)
- Maximum height, \(\mathrm{H}\)
- Range, \(\mathrm{R}\)
How To Solve Any Projectile Motion Problem (The Toolbox Method): Introducing the “Toolbox” method of solving projectile motion problems! Here we use kinematic equations and modify with initial conditions to generate a “toolbox” of equations with which to solve a classic three-part projectile motion problem.
Now, let’s look at two examples of problems involving projectile motion.
Example \(\PageIndex{1}\):
Example 1
Let’s say you are given an object that needs to clear two posts of equal height separated by a specific distance. Refer to for this example. The projectile is thrown at \(\mathrm{25 \sqrt{2}}\) m/s at an angle of 45°. If the object is to clear both posts, each with a height of 30m, find the minimum: (a) position of the launch on the ground in relation to the posts and (b) the separation between the posts. For simplicity’s sake, use a gravity constant of 10. Problems of any type in physics are much easier to solve if you list the things that you know (the “givens”).
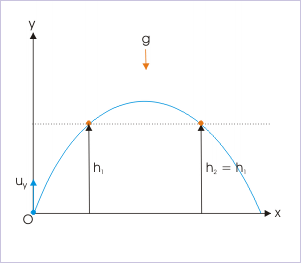
Diagram for Example 1: Use this figure as a reference to solve example 1. The problem is to make sure the object is able to clear both posts.
Solution: The first thing we need to do is figure out at what time tt the object reaches the specified height. Since the motion is in a parabolic shape, this will occur twice: once when traveling upward, and again when the object is traveling downward. For this we can use the equation of displacement in the vertical direction, \(\mathrm{y−y_0}\):
\[\mathrm{y−y_0=(v_y⋅t)−(\dfrac{1}{2}⋅g⋅t^2)}\]
We substitute in the appropriate variables:
\[\mathrm{v_y=u⋅ \sin θ=25 \sqrt{2} \dfrac{m}{s}⋅ \sin 45^{\circ}=25 \dfrac{m}{s}}\]
Therefore:
\[\mathrm{30m=25⋅t−\dfrac{1}{2}⋅10⋅t^2}\]
We can use the quadratic equation to find that the roots of this equation are 2s and 3s. This means that the projectile will reach 30m after 2s, on its way up, and after 3s, on its way down.
Example 2
An object is launched from the base of an incline, which is at an angle of 30°. If the launch angle is 60° from the horizontal and the launch speed is 10 m/s, what is the total flight time? The following information is given: \(\mathrm{u=10 \frac{m}{s}; θ=60°; g=10 \frac{m}{s^2}}\).
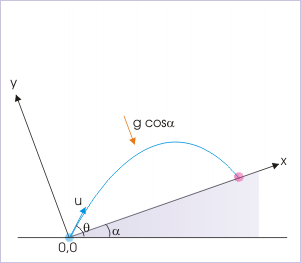
Diagram for Example 2: When dealing with an object in projectile motion on an incline, we first need to use the given information to reorient the coordinate system in order to have the object launch and fall on the same surface.
Solution: In order to account for the incline angle, we have to reorient the coordinate system so that the points of projection and return are on the same level. The angle of projection with respect to the \(\mathrm{x}\) direction is \(\mathrm{θ−α}\), and the acceleration in the \(\mathrm{y}\) direction is \(\mathrm{g⋅ \cos α}\). We replace \(\mathrm{θ}\) with \(\mathrm{θ−α}\) and \(\mathrm{g}\) with \(\mathrm{g⋅ \cos α}\):
\[\begin{align} \mathrm{T \; } & \mathrm{=\dfrac{2⋅u⋅ \sin (θ)}{g} = \dfrac{2⋅u⋅\sin (θ−α)}{g⋅ \cos (α)}=\dfrac{2⋅10⋅ \sin (60−30)}{10⋅\cos (30)} =\dfrac{20⋅ \sin (30)}{10⋅ \cos (30)} } \\ \mathrm{T \;} &\mathrm{=\dfrac{2}{\sqrt{3}}s} \end{align}\]
Zero Launch Angle
An object launched horizontally at a height \(\mathrm{H}\) travels a range \(\mathrm{v_0\sqrt{\frac{2H}{g}}}\) during a time of flight \(\mathrm{T=\sqrt{\frac{2H}{g}}}\).
learning objectives
- Explain the relationship between the range and the time of flight
Projectile motion is a form of motion where an object moves in a parabolic path. The path followed by the object is called its trajectory. Projectile motion occurs when a force is applied at the beginning of the trajectory for the launch (after this the projectile is subject only to the gravity).
One of the key components of the projectile motion, and the trajectory it follows, is the initial launch angle. The angle at which the object is launched dictates the range, height, and time of flight the object will experience while in projectile motion. shows different paths for the same object being launched at the same initial velocity and different launch angles. As illustrated by the figure, the larger the initial launch angle and maximum height, the longer the flight time of the object.

Projectile Trajectories: The launch angle determines the range and maximum height that an object will experience after being launched.This image shows that path of the same object being launched at the same speed but different angles.
We have previously discussed the effects of different launch angles on range, height, and time of flight. However, what happens if there is no angle, and the object is just launched horizontally? It makes sense that the object should be launched at a certain height (\(\mathrm{H}\)), otherwise it wouldn’t travel very far before hitting the ground. Let’s examine how an object launched horizontally at a height \(\mathrm{H}\) travels. In our case is when \(\mathrm{α}\) is 0.

Projectile motion: Projectile moving following a parabola.Initial launch angle is αα, and the velocity is \(\mathrm{v_0}\).
Duration of Flight
There is no vertical component in the initial velocity (\(\mathrm{v_0}\)) because the object is launched horizontally. Since the object travels distance \(\mathrm{H}\) in the vertical direction before it hits the ground, we can use the kinematic equation for the vertical motion:
\[\mathrm{(y−y_0)=−H=0⋅T−\dfrac{1}{2}gT^2}\]
Here, \(\mathrm{T}\) is the duration of the flight before the object its the ground. Therefore:
\[\mathrm{T=\sqrt{\dfrac{2H}{g}}}\]
Range
In the horizontal direction, the object travels at a constant speed \(\mathrm{v_0}\) during the flight. Therefore, the range \(\mathrm{R}\) (in the horizontal direction) is given as:
\[\mathrm{R=v_0⋅T=v_0\sqrt{\dfrac{2H}{g}}}\]
General Launch Angle
The initial launch angle (0-90 degrees) of an object in projectile motion dictates the range, height, and time of flight of that object.
learning objectives
- Choose the appropriate equation to find range, maximum height, and time of flight
Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning of the trajectory, after which the only interference is from gravity.
One of the key components of projectile motion and the trajectory that it follows is the initial launch angle. This angle can be anywhere from 0 to 90 degrees. The angle at which the object is launched dictates the range, height, and time of flight it will experience while in projectile motion. shows different paths for the same object launched at the same initial velocity at different launch angles. As you can see from the figure, the larger the initial launch angle, the closer the object comes to maximum height and the longer the flight time. The largest range will be experienced at a launch angle up to 45 degrees.
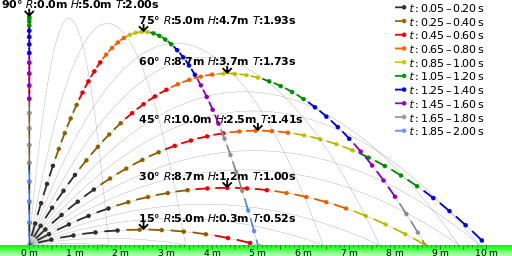
Launch Angle: The launch angle determines the range and maximum height that an object will experience after being launched. This image shows that path of the same object being launched at the same velocity but different angles.
The range, maximum height, and time of flight can be found if you know the initial launch angle and velocity, using the following equations:
\[\begin{align} \mathrm{R \;} & \mathrm{=\dfrac{v_i^2 \sin ^2 θ_i}{g}} \\ \mathrm{h \;} & \mathrm{=\dfrac{v_i^2 \sin ^2 θ_i}{2g}} \\ \mathrm{T \;} & \mathrm{=\dfrac{2v_i \sin θ}{g}} \end{align}\]
Where R – Range, h – maximum height, T – time of flight, vi – initial velocity, θi – initial launch angle, g – gravity.
Now that we understand how the launch angle plays a major role in many other components of the trajectory of an object in projectile motion, we can apply that knowledge to making an object land where we want it. If there is a certain distance, d, that you want your object to go and you know the initial velocity at which it will be launched, the initial launch angle required to get it that distance is called the angle of reach. It can be found using the following equation:
\[\mathrm{θ=\dfrac{1}{2} \sin ^{−1}(\dfrac{gd}{v^2})}\]
Key Points: Range, Symmetry, Maximum Height
Projectile motion is a form of motion where an object moves in parabolic path. The path that the object follows is called its trajectory.
learning objectives
- Construct a model of projectile motion by including time of flight, maximum height, and range
What is Projectile Motion ?
Projectile motion is a form of motion where an object moves in a bilaterally symmetrical, parabolic path. The path that the object follows is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning on the trajectory, after which the only interference is from gravity. In this atom we are going to discuss what the various components of an object in projectile motion are, we will discuss the basic equations that go along with them in another atom, “Basic Equations and Parabolic Path”
Key Components of Projectile Motion:
Time of Flight, T:
The time of flight of a projectile motion is exactly what it sounds like. It is the time from when the object is projected to the time it reaches the surface. The time of flight depends on the initial velocity of the object and the angle of the projection, θθ. When the point of projection and point of return are on the same horizontal plane, the net vertical displacement of the object is zero.
Symmetry:
All projectile motion happens in a bilaterally symmetrical path, as long as the point of projection and return occur along the same horizontal surface. Bilateral symmetry means that the motion is symmetrical in the vertical plane. If you were to draw a straight vertical line from the maximum height of the trajectory, it would mirror itself along this line.
Maximum Height, H:
The maximum height of a object in a projectile trajectory occurs when the vertical component of velocity, vyvy, equals zero. As the projectile moves upwards it goes against gravity, and therefore the velocity begins to decelerate. Eventually the vertical velocity will reach zero, and the projectile is accelerated downward under gravity immediately. Once the projectile reaches its maximum height, it begins to accelerate downward. This is also the point where you would draw a vertical line of symmetry.
Range of the Projectile, R:
The range of the projectile is the displacement in the horizontal direction. There is no acceleration in this direction since gravity only acts vertically. shows the line of range. Like time of flight and maximum height, the range of the projectile is a function of initial speed.
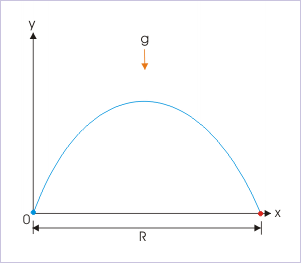
Range: The range of a projectile motion, as seen in this image, is independent of the forces of gravity.
Key Points
- Objects that are projected from, and land on the same horizontal surface will have a vertically symmetrical path.
- The time it takes from an object to be projected and land is called the time of flight. This depends on the initial velocity of the projectile and the angle of projection.
- When the projectile reaches a vertical velocity of zero, this is the maximum height of the projectile and then gravity will take over and accelerate the object downward.
- The horizontal displacement of the projectile is called the range of the projectile, and depends on the initial velocity of the object.
- When solving problems involving projectile motion, we must remember all the key components of the motion and the basic equations that go along with them.
- Using that information, we can solve many different types of problems as long as we can analyze the information we are given and use the basic equations to figure it out.
- To clear two posts of equal height, and to figure out what the distance between these posts is, we need to remember that the trajectory is a parabolic shape and that there are two different times at which the object will reach the height of the posts.
- When dealing with an object in projectile motion on an incline, we first need to use the given information to reorientate the coordinate system in order to have the object launch and fall on the same surface.
- For the zero launch angle, there is no vertical component in the initial velocity.
- The duration of the flight before the object hits the ground is given as \(\mathrm{T=\sqrt{\frac{2H}{g}}}\).
- In the horizontal direction, the object travels at a constant speed v0 during the flight. The range R (in the horizontal direction) is given as: \(\mathrm{R=v_0⋅T=v_0\sqrt{\dfrac{2H}{g}}}\).
- If the same object is launched at the same initial velocity, the height and time of flight will increase proportionally to the initial launch angle.
- An object launched into projectile motion will have an initial launch angle anywhere from 0 to 90 degrees.
- The range of an object, given the initial launch angle and initial velocity is found with: \(\mathrm{R=\dfrac{v_i^2 \sin ^2 θ_i}{g}}\).
- The maximum height of an object, given the initial launch angle and initial velocity is found with: \(\mathrm{h=\dfrac{v_i^2 \sin ^2 θ_i}{2g}}\).
- The time of flight of an object, given the initial launch angle and initial velocity is found with: \(\mathrm{T=\dfrac{2v_i \sin θ}{g}}\) .
- The angle of reach is the angle the object must be launched at in order to achieve a specific distance: \(\mathrm{θ=\dfrac{1}{2} \sin ^{−1}(\dfrac{gd}{v^2})}\).
- Objects that are projected from and land on the same horizontal surface will have a path symmetric about a vertical line through a point at the maximum height of the projectile.
- The time it takes from an object to be projected and land is called the time of flight. It depends on the initial velocity of the projectile and the angle of projection.
- The maximum height of the projectile is when the projectile reaches zero vertical velocity. From this point the vertical component of the velocity vector will point downwards.
- The horizontal displacement of the projectile is called the range of the projectile and depends on the initial velocity of the object.
- If an object is projected at the same initial speed, but two complementary angles of projection, the range of the projectile will be the same.
Key Terms
- trajectory: The path of a body as it travels through space.
- symmetrical: Exhibiting symmetry; having harmonious or proportionate arrangement of parts; having corresponding parts or relations.
- reorientate: to orientate anew; to cause to face a different direction
- gravity: Resultant force on Earth’s surface, of the attraction by the Earth’s masses, and the centrifugal pseudo-force caused by the Earth’s rotation.
- bilateral symmetry: the property of being symmetrical about a vertical plane
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Sunil Kumar Singh, Features of Projectile Motion. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Projectile motion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Projectile_motion. License: CC BY-SA: Attribution-ShareAlike
- trajectory. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/trajectory. License: CC BY-SA: Attribution-ShareAlike
- symmetrical. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/symmetrical. License: CC BY-SA: Attribution-ShareAlike
- Projectiles at an Angle. Located at: http://www.youtube.com/watch?v=4jNE3eTVEgo. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Sunil Kumar Singh, Features of Projectile Motion. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Sunil Kumar Singh, Projectile Motion on an Incline. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14614/latest/. License: CC BY: Attribution
- reorientate. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/reorientate. License: CC BY-SA: Attribution-ShareAlike
- Projectiles at an Angle. Located at: http://www.youtube.com/watch?v=4jNE3eTVEgo. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Sunil Kumar Singh, Projectile Motion on an Incline. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14614/latest/. License: CC BY: Attribution
- How To Solve Any Projectile Motion Problem (The Toolbox Method). Located at: http://www.youtube.com/watch?v=M8xCj2VPHas. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Sunil Kumar Singh, Features of Projectile Motion. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Trajectory of a projectile. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Trajectory_of_a_projectile. License: CC BY-SA: Attribution-ShareAlike
- Trajectory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Trajectory. License: CC BY-SA: Attribution-ShareAlike
- trajectory. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/trajectory. License: CC BY-SA: Attribution-ShareAlike
- Projectiles at an Angle. Located at: http://www.youtube.com/watch?v=4jNE3eTVEgo. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Sunil Kumar Singh, Projectile Motion on an Incline. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14614/latest/. License: CC BY: Attribution
- How To Solve Any Projectile Motion Problem (The Toolbox Method). Located at: http://www.youtube.com/watch?v=M8xCj2VPHas. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Ideal projectile motion for different angles. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Ideal_projectile_motion_for_different_angles.svg. License: CC BY-SA: Attribution-ShareAlike
- Ferde hajitas1. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Ferde_hajitas1.svg. License: CC BY-SA: Attribution-ShareAlike
- Trajectory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Trajectory. License: CC BY-SA: Attribution-ShareAlike
- Trajectory of a projectile. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Trajectory_of_a_projectile. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Features of Projectile Motion. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- trajectory. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/trajectory. License: CC BY-SA: Attribution-ShareAlike
- Projectiles at an Angle. Located at: http://www.youtube.com/watch?v=4jNE3eTVEgo. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Sunil Kumar Singh, Projectile Motion on an Incline. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14614/latest/. License: CC BY: Attribution
- How To Solve Any Projectile Motion Problem (The Toolbox Method). Located at: http://www.youtube.com/watch?v=M8xCj2VPHas. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Ideal projectile motion for different angles. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Ideal_projectile_motion_for_different_angles.svg. License: CC BY-SA: Attribution-ShareAlike
- Ferde hajitas1. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Ferde_hajitas1.svg. License: CC BY-SA: Attribution-ShareAlike
- Ideal projectile motion for different angles. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Ideal_projectile_motion_for_different_angles.svg. License: CC BY-SA: Attribution-ShareAlike
- bilateral symmetry. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/bilateral_symmetry. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Features of Projectile Motion. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Projectile motion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Projectile_motion. License: CC BY-SA: Attribution-ShareAlike
- gravity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/gravity. License: CC BY-SA: Attribution-ShareAlike
- trajectory. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/trajectory. License: CC BY-SA: Attribution-ShareAlike
- Projectiles at an Angle. Located at: http://www.youtube.com/watch?v=4jNE3eTVEgo. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Sunil Kumar Singh, Projectile Motion on an Incline. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14614/latest/. License: CC BY: Attribution
- How To Solve Any Projectile Motion Problem (The Toolbox Method). Located at: http://www.youtube.com/watch?v=M8xCj2VPHas. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Features of Projectile Motion. February 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution
- Ideal projectile motion for different angles. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Ideal_projectile_motion_for_different_angles.svg. License: CC BY-SA: Attribution-ShareAlike
- Ferde hajitas1. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Ferde_hajitas1.svg. License: CC BY-SA: Attribution-ShareAlike
- Ideal projectile motion for different angles. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/File:Ideal_projectile_motion_for_different_angles.svg. License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Features of Projectile Motion. January 25, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m13847/latest/. License: CC BY: Attribution

