12.2: Introduction
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18288

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Describe gas using the kinetic theory of gases
Introduction to Temperature and Kinetic Theory
The kinetic theory of gases describes a gas as a large number of small particles (atoms or molecules), all of which are in constant, random motion. The rapidly moving particles constantly collide with each other, and with the walls of the container. Kinetic theory explains macroscopic properties of gases (such as pressure, temperature, and volume) by considering their molecular composition and motion. Essentially, the theory posits that pressure is due not to static repulsion between molecules (as was Isaac Newton’s conjecture) but rather due to collisions between molecules moving at different velocities through Brownian motion. Also, the temperature of an ideal monatomic gas is a measure of the average kinetic energy of its atoms, as illustrated in.
Translational Motion of Helium: Real gases do not always behave according to the ideal model under certain conditions, such as high pressure. Here, the size of helium atoms relative to their spacing is shown to scale under 1950 atmospheres of pressure.
The kinetic theory of gases uses the model of the ideal gas to relate temperature to the average translational kinetic energy of the molecules in a container of gas in thermodynamic equilibrium. Classical mechanics defines the translational kinetic energy of a gas molecule as follows:
Ek=12mv2,
where m is the particle mass and v its speed (the magnitude of its velocity). The distribution of the speeds (which determine the translational kinetic energies) of the particles in a classical ideal gas is called the Maxwell-Boltzmann distribution. In kinetic theory, the temperature of a classical ideal gas is related to its average kinetic energy per degree of freedom Ek via the equation:
ˉEk=12kT,
(k: Boltzmann’s constant). We will derive this relationship in the following atoms. We will also derive the ideal gas law:
pV=nRT,
(R: ideal gas constant, n: number of moles of gas) from a microscopic theory.
Atomic Theory of Matter
Atomic theory is a scientific theory of the nature of matter which states that matter is composed of discrete units called atoms.
learning objectives
- Formulate five postulates of John Dalton’s atomic theory
Atomic theory is a scientific theory of the nature of matter which states that matter is composed of discrete units called atoms, as opposed to the obsolete notion that matter could be divided into any arbitrarily small quantity. Although physicists discovered that the so-called “indivisible atom” was actually a conglomerate of various subatomic particles, the concept of atoms is still important because they are building blocks of matter and form the basis of chemistry.

Illustration of the Helium Atom: This is an illustration of the helium atom, depicting the nucleus (pink) and the electron cloud distribution (black). The nucleus (upper right) in helium-4 is in reality spherically symmetric and closely resembles the electron cloud, although for more complicated nuclei this is not always the case. The black bar is one angstrom (10-10 m, or 100 pm).
Dalton’s Atomic Hypothesis
Philosophical proposals regarding atoms have been suggested since the years of the ancient Greeks, but John Dalton was the first to propose a scientific theory of atoms. He based his study on two laws about chemical reactions that emerged (without referring to the notion of an atomic theory) in the late 18thcentury. The first was the law of conservation of mass, formulated by Antoine Lavoisier in 1789, which states that the total mass in a chemical reaction remains constant (that is, the reactants have the same mass as the products). The second was the law of definite proportions, first proven by the French chemist Joseph Louis Proust.
Dalton proposed that each chemical element is composed of atoms of a single, unique type, and though they cannot be altered or destroyed by chemical means, they can combine to form more complex structures (chemical compounds). This marked the first truly scientific theory of the atom, since Dalton reached his conclusions by experimentation and examination of the results in an empirical fashion. For this reason, Dalton is considered the originator of modern atomic theory.
5 Main Points
Dalton’s atomic theory had 5 main points:
- Elements are made of extremely small particles called atoms.
- Atoms of a given element are identical in size, mass, and other properties; atoms of different elements differ in size, mass, and other properties.
- Atoms cannot be subdivided, created, or destroyed.
- Atoms of different elements combine in simple whole-number ratios to form chemical compounds.
- In chemical reactions, atoms are combined, separated, or rearranged.
Of these five, only three are still considered valid today. 1, 4, and 5 are valid, while 2 and 3 have turned out not to be the case. Atoms can be broken down into smaller pieces, and atoms of a given element can vary in mass and other properties (see isotopes and ions).
Knowing that a gas is composed of small atomic and molecular particles, it is natural to try to explain properties of the gas from a microscopic point of view. This effort led to the development of the kinetic theory of gases, where macroscopic properties of gases, such as pressure, temperature, and volume, are explained by considering their molecular composition and motion.
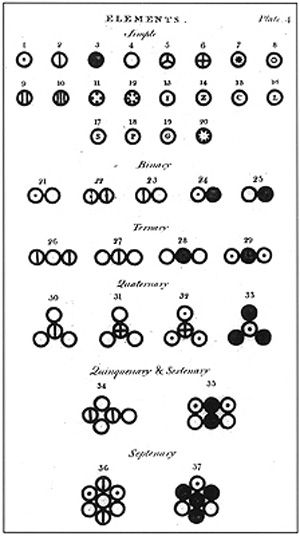
John Dalton’s A New System of Chemical Philosophy: Various atoms and molecules as depicted in John Dalton’s A New System of Chemical Philosophy (1808).
Key Points
- The kinetic theory posits that pressure is due to collisions between molecules moving at different velocities through Brownian motion.
- The temperature of an ideal monatomic gas is a measure of the average kinetic energy of its atoms. In kinetic theory, it is related to its average kinetic energy per degree of freedom Ek via the equation: ˉEk=12kT.
- The kinetic theory of gases uses the model of the ideal gas to relate temperature to the average translational kinetic energy of the molecules in a container of gas in thermodynamic equilibrium.
- John Dalton was the first to propose a scientific theory of atoms. He based his study on two laws: the law of conservation of mass and the law of definite proportions.
- Dalton proposed that each chemical element is composed of atoms of a single, unique type, and though they cannot be altered or destroyed by chemical means, they can combine to form more complex structures.
- Kinetic theory of gases explain macroscopic properties of gases, such as pressure, temperature, and volume, by considering their molecular composition and motion.
- While Dalton’s idea of matter being composed of various atoms was correct, he was wrong about some of their properties. Atoms can be broken down into smaller parts. Atoms of the same element can have slightly different masses and behave differently. See isotopes and ions for examples.
Key Terms
- ideal gas: A hypothetical gas whose molecules exhibit no interaction and undergo elastic collision with each other and with the walls of the container.
- degree of freedom: Any of the coordinates, a minimum number of which are needed to specify the motion of a mechanical system.
- Brownian motion: Random motion of particles suspended in a fluid, arising from those particles being struck by individual molecules of the fluid.
- atom: The smallest possible amount of matter which still retains its identity as a chemical element, now known to consist of a nucleus surrounded by electrons.
- kinetic theory of gases: The kinetic theory of gases describes a gas as a large number of small particles (atoms or molecules), all of which are in constant, random motion.
- chemical reaction: A process, involving the breaking or making of interatomic bonds, in which one or more substances are changed into others.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- ideal gas. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/ideal_gas. License: CC BY-SA: Attribution-ShareAlike
- degree of freedom. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/degree_of_freedom. License: CC BY-SA: Attribution-ShareAlike
- Temperature. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Temperature%23Kinetic_theory_of_gases. License: CC BY-SA: Attribution-ShareAlike
- Kinetic theory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Kinetic_theory%23Temperature_and_kinetic_energy. License: CC BY-SA: Attribution-ShareAlike
- Brownian motion. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/Brownian_motion. License: CC BY-SA: Attribution-ShareAlike
- Kinetic theory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Kinetic_theory. License: Public Domain: No Known Copyright
- chemical reaction. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/chemical_reaction. License: CC BY-SA: Attribution-ShareAlike
- Atomic theory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Atomic_theory. License: CC BY-SA: Attribution-ShareAlike
- Kinetic theory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Kinetic_theory. License: CC BY-SA: Attribution-ShareAlike
- kinetic theory of gases. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/kinetic%20theory%20of%20gases. License: CC BY-SA: Attribution-ShareAlike
- atom. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/atom. License: CC BY-SA: Attribution-ShareAlike
- Kinetic theory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Kinetic_theory. License: Public Domain: No Known Copyright
- Atom. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Atom. License: CC BY: Attribution
- John Dalton. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/John_Dalton. License: Public Domain: No Known Copyright

