12.5: Ideal Gas Law
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18291

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Describe how ideal gas law was derived.
The ideal gas law is the equation of state of a hypothetical ideal gas (an illustration is offered in ). In an ideal gas, there is no molecule-molecule interaction, and only elastic collisions are allowed. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle’s law and Charles’ law.
Atoms and Modules in a Gas: Atoms and molecules in a gas are typically widely separated, as shown. Because the forces between them are quite weak at these distances, they are often described by the ideal gas law.
Empirical Derivation
Boyle’s law states that pressure P and volume V of a given mass of confined gas are inversely proportional:
P∝1V,
while Charles’ law states that volume of a gas is proportional to the absolute temperature T of the gas at constant pressure
V∝T.
By combining the two laws, we get
PVT=C,
where C is a constant which is directly proportional to the amount of gas, n (representing the number of moles).
The proportionality factor is the universal gas constant, R, i.e. C=nR.
Hence the ideal gas law
PV=nRT
Equivalently, it can be written as PV=NkT,
where k is Boltzmann’s constant and N is the number of molecules.
(Since N = nNA, you can see that R=NAk, where NA is Avogadro’s number. )
Note that the empirical derivation does not consider microscopic details. However, the equation can be derived from first principles in the classical thermodynamics (which goes beyond the scope of this Atom ).
Microscopic version
We have seen in the Atom on “Origin of Pressure” that
P=Nm¯v23V,
where P is the pressure, N is the number of molecules, m is the mass of the molecule, v is the speed of molecules, and V is the volume of the gas. Therefore, we derive a microscopic version of the ideal gas law
PV=13Nm¯v2
Isotherms
An isothermal process is a change of a system in which the temperature remains constant: ΔT=0.
learning objectives
- Identify conditions at which isothermal processes can occur.
An isothermal process is a change of a system in which the temperature remains constant: ΔT = 0. Typically this occurs when a system is in contact with an outside thermal reservoir (heat bath), and the change occurs slowly enough to allow the system to adjust continually to the temperature of the reservoir through heat exchange. In contrast, an adiabatic process occurs when a system exchanges no heat with its surroundings (Q = 0). In other words, in an isothermal process, the value ΔT = 0 but Q ≠ 0, while in an adiabatic process, ΔT ≠ 0 but Q = 0.
For an ideal gas, the product PV (P: pressure, V: volume) is a constant if the gas is kept at isothermal conditions (Boyle’s law). According to the ideal gas law, the value of the constant is NkT, where N is the number of molecules of gas and k is Boltzmann’s constant.
This means that p=NkTV=ConstantV holds.
The family of curves generated by this equation is shown in the graph presented in. Each curve is called an isotherm. Such graphs are termed indicator diagrams—first used by James Watt and others to monitor the efficiency of engines. The temperature corresponding to each curve in the figure increases from the lower left to the upper right.
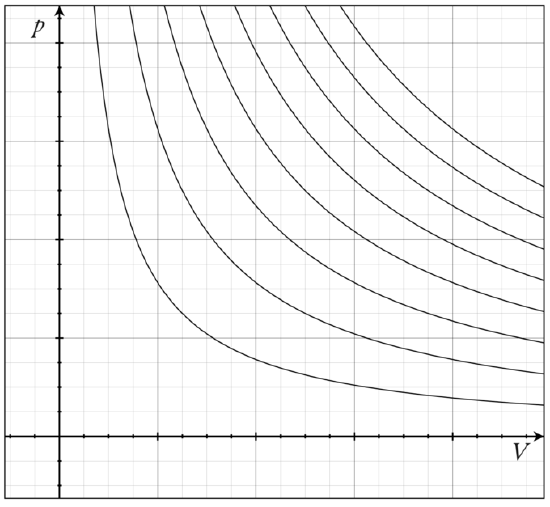
Isotherms of an Ideal Gas: Several isotherms of an ideal gas on a PV diagram.
Calculation of Work
In thermodynamics, the work involved when a gas changes from state A to state B is simply:
WA→B=∫VBVAPdV.
(This equation is derived in our Atom on “Constant Pressure” under kinetic theory. Note that P=FA. This definition is consistent with our definition of work being force times distance. )
For an isothermal, reversible process, this integral equals the area under the relevant pressure-volume isotherm, and is indicated in blue in for an ideal gas. Again, P=nRTV applies and with T being constant (as this is an isothermal process), we have:
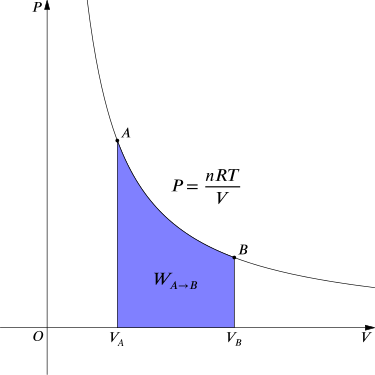
Work Done by Gas During Expansion: The blue area represents “work” done by the gas during expansion for this isothermal change.
WA→B=∫VBVApdV=∫VBVANkTVdV=NkTlnVBVA.
By convention, work is defined as the work the system does on its environment. If, for example, the system expands by a piston moving in the direction of force applied by the internal pressure of a gas, then the work is counted as positive. As this work is done by using internal energy of the system, the result is that the internal energy decreases. Conversely, if the environment does work on the system so that its internal energy increases, the work is counted as negative (for details on internal energy, check our Atom on “Internal Energy of an Ideal Gas”).
Constant Pressure
Isobaric processis a thermodynamic process in which the pressure stays constant (at constant pressure, work done by a gas is PΔV).
learning objectives
- Describe behavior of monatomic gas during isobaric processes.
Under a certain constraint (e.g., pressure), gases can expand or contract; depending on the type of constraint, the final state of the gas may change. For example, an ideal gas that expands while its temperature is kept constant (called isothermal process) will exist in a different state than a gas that expands while pressure stays constant (called isobaric process). This Atom addresses isobaric process and correlated terms. We will discuss isothermal process in a subsequent Atom.
Isobaric Process
An isobaric process is a thermodynamic process in which pressure stays constant: ΔP=0. For an ideal gas, this means the volume of a gas is proportional to its temperature (historically, this is called Charles’ law ). Let’s consider a case in which a gas does work on a piston at constant pressure P, referring to Fig 1 as illustration. Since the pressure is constant, the force exerted is constant and the work done is given as W=Fd, where F (=PA) is the force on the piston applied by the pressure and d is the displacement of the piston. Therefore, the work done by the gas (W) is:
W=PAd
Because the change in volume of a cylinder is its cross-sectional area A times the displacement d, we see that Ad=ΔV, the change in volume. Thus,
W=PΔV
(as seen in Fig 2—isobaric process ). Note: if ΔV is positive, then W is positive, meaning that work is done by the gas on the outside world. Using the ideal gas law PV=NkT(P=const),
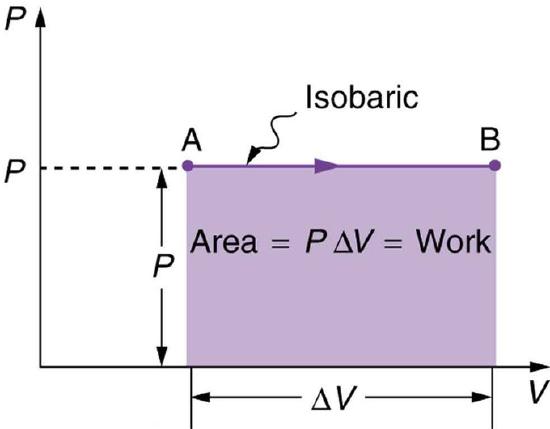
Fig 2: A graph of pressure versus volume for a constant-pressure, or isobaric process. The area under the curve equals the work done by the gas, since W=PΔV.
W=NkΔT
(Eq. 1) for an ideal gas undergoing an isobaric process.
Monatomic Gas
According to the first law of thermodynamics,
Q=ΔU+W
(Eq. 2), where W is work done by the system, U is internal energy, and Q is heat. The law says that the heat transferred to the system does work but also changes the internal energy of the system. Since,
U=32NkT for a monatomic gas, we get ΔU=32NkΔT
(Eq. 3; for the details on internal energy, see our Atom on “Internal Energy of an Ideal Gas”). By using the Equations 1 and 3, Eq. 2 can be written as:
Q=52NkΔT for monatomic gas in an isobaric process.
Specific Heat
Specific heat at constant pressure is defined by the following equation:
Q=ncPΔT
Here n is the amount of particles in a gas represented in moles. By noting that N=NAn and R=kNA (NA: Avogadro’s number, R: universal gas constant), we derive:
cP=52kNA=52R for a monatomic gas.
Problem Solving
With the ideal gas law we can figure pressure, volume or temperature, and the number of moles of gases under ideal thermodynamic conditions.
learning objectives
- Identify steps used to solve the ideal gas equation.
The Ideal Gas Law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It is most accurate for monatomic gases at high temperatures and low pressures.
The ideal gas law has the form:
PV=nRT,
where R is the universal gas constant, and with it we can find values of the pressure P, volume V, temperature T, or number of moles n under a certain ideal thermodynamic condition. Typically, you are given enough parameters to calculate the unknown. Variations of the ideal gas equation may help solving the problem easily. Here are some general tips.
The ideal gas law can also come in the form:
PV=NkT,
where N is the number of particles in the gas and k is the Boltzmann constant.
To solve the ideal gas equation:
- Write down all the information that you know about the gas.
- If necessary, convert the known values to SI units.
- Choose a relevant gas law equation that will allow you to calculate the unknown variable.
- Substitute the known values into the equation. Calculate the unknown variable.
Remember that the general gas equation only applies if the molar quantity of the gas is fixed. For example, if a gas is mixed with another gas, you may have to apply the equation separately for individual gases.
Example
Let’s imagine that at the beginning of a journey a truck tire has a volume of 30,000 cm3 and an internal pressure of 170 kPa. The temperature of the tire is 16∘C. By the end of the trip, the volume of the tire has increased to 32,000 cm3 and the temperature of the air inside the tire is 40∘C. What is the tire pressure at the end of the journey?

Tire Pressure: Tire pressure may change significantly during the operation of the vehicle. This is mostly due to the temperature change of the air in tires.
Solution:
Step 1. Write down all the information that you know about the gas: P1= 170 kPa and P2 is unknown. V1 = 30,000 cm3 and V2 = 32,000 cm3. T1 = 16∘C and T2 = 40∘C.
Step 2. Convert the known values to SI units if necessary: Here, temperature must be converted into Kelvin. Therefore, T1 = 16 + 273 = 289 K, T2 = 40 + 273 = 313 K
Step 3. Choose a relevant gas law equation that will allow you to calculate the unknown variable: We can use the general gas equation to solve this problem: P1V1T1=P2V2T2.
Therefore, P2=P1×V1×T2T1×V2.
Step 4. Substitute the known values into the equation. Calculate the unknown variable:
P2=170×30,000×313289×32,000=173kPa
The pressure of the tire at the end of the journey is 173 kPa.
Note that in Step 2 we did not bother to convert the volume values to m3. In Step 4, pressure appears both in the numerator and denominator. In this case the conversion was not necessary.
Avogador’s Number
The number of molecules in a mole is called Avogadro’s number (NA)—defined as 6.02x 1023 mol-1.
learning objectives
- Explain relationship between Avogadro’s number and mole.
When measuring the amount of substance, it is sometimes easier to work with a unit other than the number of molecules. A mole (abbreviated mol) is a base unit in the International System of Units (SI). It is defined as any substance containing as many atoms or molecules as there are in exactly 12 grams (0.012 kg) of carbon-12. The actual number of atoms or molecules in one mole is called Avogadro’s constant (NA), in recognition of Italian scientist Amedeo Avogadro.

Amadeo Avogadro: Amedeo Avogadro (1776–1856). He established the relationship between the masses of the same volume of different gases (at the same temperature and pressure) corresponds to the relationship between their respective molecular weights.
Avogadro’s number (N) refers to the number of molecules in one gram-molecule of oxygen. This indicates an amount of substance as opposed to an independent dimension of measurement. In 1811 Amedeo Avogadro first proposed that the volume of a gas (at a given pressure and temperature) is proportional to the number of atoms or molecules, regardless of the nature of the gas (i.e., this number is universal and independent of the type of gas). In 1926, Jean Perrin won the Nobel Prize in Physics, largely for his work in determining the Avogadro constant (by several different methods). The value of Avogadro’s constant, NA , has been found to equal 6.02×1023mol−1.
Role in Science
Avogadro’s constant is a scaling factor between macroscopic and microscopic (atomic scale) observations of nature. As such, it provides the relation between other physical constants and properties. For example, it establishes a relationship between the gas constant R and the Boltzmann constant k,
R=kNA=8.314472(15)Jmol−1K−1;
and the Faraday constant F and the elementary charge e,
F=NAe=96485.3383(83)Cmol−1.
Measuring NA
The determination of NA is crucial to the calculation of an atom’s mass, since the latter is obtained by dividing the mass of a mole of the gas by Avogadro’s constant. In his study on Brownian motion in 1905, Albert Einstein proposed that this constant could be determined based on the quantities observable in Brownian motion. Subsequently, Einstein’s idea was verified, leading to the first determination of NA in 1908 through the experimental work of Jean Baptiste Perrin.
Absolute Temperature
Absolute temperature is the most commoly used thermodyanmic temperature unit and is the standard unit of temperature.
learning objectives
- Describe relationship between absolute temperature and kinetic energy.
Thermodynamic temperature is the absolute measure of temperature. It is one of the principal parameters of thermodynamics and kinetic theory of gases. Thermodynamic temperature is an “absolute” scale because it is the measure of the fundamental property underlying temperature: its null or zero point (“absolute zero”) is the temperature at which the particle constituents of matter have minimal motion and cannot become any colder. That is, they have minimal motion, retaining only quantum mechanical motion, as diagramed in.
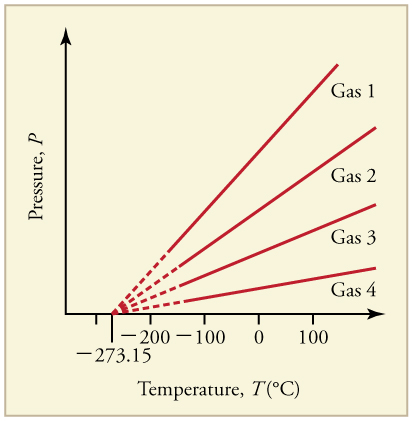
Graph of Pressure Versus Temperature: Graph of pressure versus temperature for various gases kept at a constant volume. Note that all of the graphs extrapolate to zero pressure at the same temperature
At its simplest, “temperature” arises from the kinetic energy of the random motions of matter’s particle constituents such as molecules or atoms, as seen in. Therefore, it is reasonable to choose absolute zero, where all classical motion ceases, as the reference point (T=0) of our temperature system. By using the absolute temperature scale (Kelvin system), which is the most commonly used thermodynamic temperature, we have shown that the average translational kinetic energy (KE) of a particle in a gas has a simple relationship to the temperature:
Translational Motion of Helium: Real gases do not always behave according to the ideal model under certain conditions, such as high pressure. Here, the size of helium atoms relative to their spacing is shown to scale under 1950 atmospheres of pressure.
¯KE=32kT.
Note that this equation would not look this elegant if the Fahrenheit scale were used instead.
The Kelvin scale
The kelvin (or “absolute temperature”) is the standard thermodyanmic temperature unit. It is one of the seven base units in the International System of Units (SI) and is assigned the unit symbol K. By international agreement, the unit kelvin and its scale are defined by two points: absolute zero and the triple point of Vienna Standard Mean Ocean Water (water with a specified blend of hydrogen and oxygen isotopes). Absolute zero, the lowest possible temperature, is defined precisely as 0 K and −273.15 °C. The triple point of water is defined precisely as 273.16 K and 0.01 °C.
Key Points
- Ideal gas law was derived empirically by combining Boyle’s law and Charles’ law.
- Although the empirical derivation of the equation does not consider microscopic details, the ideal gas law can be derived from first principles in the classical thermodynamics.
- Pressure and volume of a gas can be related to the average velocity of molecues: PV=13Nm¯v2.
- Isothermal processes typically occur when a system is in contact with an outside thermal reservoir ( heat bath), and the change occurs slowly enough to allow the system to adjust continually to the temperature of the reservoir through heat exchange.
- For an ideal gas, from the ideal gas law PV=NkT,PV remains constant through an isothermal process. A curve in a P-V diagram generated by the equation PV=const is called an isotherm.
- For an isothermal, reversible process, the work done by the gas is equal to the area under the relevant pressure -volume isotherm. It is given as WA→B=NkTlnVBVA.
- Gases can expand or contract under a certain constraint. Depending on the constraint, the final state of the gas may change.
- The heat transferred to the system does work but also changes the internal energy of the system. In an isobaric process for a monatomic gas, heat and the temperature change satisfy the following equation: Q=52NkΔT.
- For a monatomic ideal gas, specific heat at constant pressure is 52R.
- Write down all the information that you know about the gas and convert the known values to SI units if necessary.
- Choose a relevant gas law equation that will allow you to calculate the unknown variable, and substitute the known values into the equation. Then calculate the unknown variable.
- The general gas equation only applies if the molar quantity of the gas is fixed.
- Avogadro hypothesized that equal volumes of gas, at the same pressure and temperature, contain equal numbers of molecules, regardless of the type of gas.
- Avogadro’s constant is a scaling factor between macroscopic and microscopic (atomic scale) observations of nature. It provides the relation between other physical constants and properties.
- Albert Einstein proposed that Avogadro’s number could be determined based on the quantities observable in Brownian motion. NA was measured for the first time by Jean Baptiste Perrin in 1908.
- Temperature arises from the kinetic energy of the random motions of matter ‘s particle constituents such as molecules or atoms. Therefore, it is reasonable to choose absolute zero, where all classical motion ceases, as the reference point.
- By international agreement, the unit kelvin and its scale are defined by two points: absolute zero and the triple point of the standardized water.
- At absolute zero, the particle constituents of matter have minimal motion and cannot become any colder. They retain minimal, quantum mechanical motion.
Key Terms
- mole: In the International System of Units, the base unit of amount of substance; the amount of substance of a system which contains as many elementary entities as there are atoms in 12 g of carbon-12. Symbol: mol.
- ideal gas: A hypothetical gas whose molecules exhibit no interaction and undergo elastic collision with each other and with the walls of the container.
- Avogadro’s number: the number of constituent particles (usually atoms or molecules) in one mole of a given substance. It has dimensions of reciprocal mol and its value is equal to 6.02214129·1023 mol-1
- adiabatic: Occurring without gain or loss of heat.
- internal energy: The sum of all energy present in the system, including kinetic and potential energy; equivalently, the energy needed to create a system, excluding the energy necessary to displace its surroundings.
- the first law of thermodynamics: A version of the law of energy conservation: the change in the internal energy of a closed system is equal to the amount of heat supplied to the system, minus the amount of work done by the system on its surroundings.
- specific heat: The ratio of the amount of heat needed to raise the temperature of a unit mass of substance by a unit degree to the amount of heat needed to raise that of the same mass of water by the same amount.
- SI units: International System of Units (abbreviated SI from French: Le Système international d’unités). It is the modern form of the metric system.
- gas constant: A universal constant, R, that appears in the ideal gas law, (PV = nRT), derived from two fundamental constants, the Boltzman constant and Avogadro’s number, (R = NAk).
- Faraday constant: The magnitude of electric charge per mole of electrons.
- Brownian motion: Random motion of particles suspended in a fluid, arising from those particles being struck by individual molecules of the fluid.
- absolute zero: The coldest possible temperature: zero on the Kelvin scale and approximately -273.15°C and -459.67°F. The total absence of heat; the temperature at which motion of all molecules would cease.
- International System of Units: (SI): The standard set of basic units of measurement used in scientific literature worldwide.
- Vienna Standard Mean Ocean Water: A standard defining a standardized isotopic composition of water.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- ideal gas. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/ideal_gas. License: CC BY-SA: Attribution-ShareAlike
- Ideal gas law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Ideal_gas_law%23Empirical. License: CC BY-SA: Attribution-ShareAlike
- Avogadro's number. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Avogadro's%20number. License: CC BY-SA: Attribution-ShareAlike
- mole. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/mole. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Ideal Gas Law. February 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42216/latest/. License: CC BY: Attribution
- ideal gas. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/ideal_gas. License: CC BY-SA: Attribution-ShareAlike
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/internal-energy. License: CC BY-SA: Attribution-ShareAlike
- adiabatic. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/adiabatic. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Ideal Gas Law. February 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42216/latest/. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- OpenStax College, The First Law of Thermodynamics and Some Simple Processes. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42233/latest/. License: CC BY: Attribution
- Isobaric process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isobaric_process. License: CC BY-SA: Attribution-ShareAlike
- the first law of thermodynamics. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/the%20first%20law%20of%20thermodynamics. License: CC BY-SA: Attribution-ShareAlike
- specific heat. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/specific_heat. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Ideal Gas Law. February 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42216/latest/. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- OpenStax College, The First Law of Thermodynamics and Some Simple Processes. February 5, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42233/latest/. License: CC BY: Attribution
- ideal gas. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/ideal_gas. License: CC BY-SA: Attribution-ShareAlike
- Ideal gas law. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Ideal_gas_law. License: CC BY-SA: Attribution-ShareAlike
- Free High School Science Texts Project, Thermal Properties and Ideal Gases: Ideal Gas Law and General Gas Equation. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m39086/latest/. License: CC BY: Attribution
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/si-units. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Ideal Gas Law. February 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42216/latest/. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- OpenStax College, The First Law of Thermodynamics and Some Simple Processes. February 5, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42233/latest/. License: CC BY: Attribution
- Tire. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Tire. License: CC BY: Attribution
- Brownian motion. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/Brownian_motion. License: CC BY-SA: Attribution-ShareAlike
- Avogadro constant. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Avogadro_constant%23Measurement. License: CC BY-SA: Attribution-ShareAlike
- Brownian motion. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Brownian_motion. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Ideal Gas Law. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42216/latest/. License: CC BY: Attribution
- Faraday constant. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Faraday%20constant. License: CC BY-SA: Attribution-ShareAlike
- gas constant. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/gas_constant. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Ideal Gas Law. February 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42216/latest/. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- OpenStax College, The First Law of Thermodynamics and Some Simple Processes. February 5, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42233/latest/. License: CC BY: Attribution
- Tire. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Tire. License: CC BY: Attribution
- Avogadro Amedeo. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Avogadro_Amedeo.jpg. License: CC BY-SA: Attribution-ShareAlike
- absolute zero. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/absolute_zero. License: CC BY-SA: Attribution-ShareAlike
- Thermodynamic temperature. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Thermodynamic_temperature. License: CC BY-SA: Attribution-ShareAlike
- International System of Units. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/International%20System%20of%20Units. License: CC BY-SA: Attribution-ShareAlike
- Vienna Standard Mean Ocean Water. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/Vienna_Standard_Mean_Ocean_Water. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, The Ideal Gas Law. February 4, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42216/latest/. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- Isothermal process. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Isothermal_process. License: CC BY: Attribution
- OpenStax College, The First Law of Thermodynamics and Some Simple Processes. February 5, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42233/latest/. License: CC BY: Attribution
- Tire. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/Tire. License: CC BY: Attribution
- Avogadro Amedeo. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Avogadro_Amedeo.jpg. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, Temperature. April 28, 2014. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42214/latest/. License: CC BY: Attribution
- Kinetic theory. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Kinetic_theory. License: Public Domain: No Known Copyright

