6.9: Direct-Current Circuits (Answers)
- Page ID
- 100369
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
1. Some of the energy being used to recharge the battery will be dissipated as heat by the internal resistance.
3. \(\displaystyle P=I^2R=(\frac{ε}{r+R})^2R=ε^2R(r+R)^{−2},\frac{dP}{dR}=ε^2[(r+R)^{−2}−2R(r+R)^{−3}]=0\) \(\displaystyle [\frac{(r+R)−2R}{(r+R)^3}]=0,r=R\)
5. It would probably be better to be in series because the current will be less than if it were in parallel.
7. two filaments, a low resistance and a high resistance, connected in parallel
9. It can be redrawn.
\(\displaystyle R_{eq}=[\frac{1}{R_6}+\frac{1}{R_1}+\frac{1}{R_2+(\frac{1}{R_4}+\frac{1}{R_3+R+5})^{−1}}]^{−1}\).
11. In series the voltages add, but so do the internal resistances, because the internal resistances are in series. In parallel, the terminal voltage is the same, but the equivalent internal resistance is smaller than the smallest individual internal resistance and a higher current can be provided.
13. The voltmeter would put a large resistance in series with the circuit, significantly changing the circuit. It would probably give a reading, but it would be meaningless.
15. The ammeter has a small resistance; therefore, a large current will be produced and could damage the meter and/or overheat the battery.
19. Not only might water drip into the switch and cause a shock, but also the resistance of your body is lower when you are wet.
Problems
21. a.
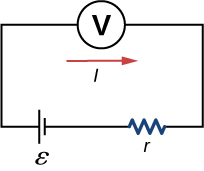
b. 0.476W;
c. 0.691 W;
d. As \(\displaystyle R_L\) is lowered, the power difference decreases; therefore, at higher volumes, there is no significant difference.
23. a. \(\displaystyle 0.400Ω\);
b. No, there is only one independent equation, so only r can be found.
25. a. \(\displaystyle 0.400Ω\);
b. 40.0 W;
c. \(\displaystyle 0.0956°C/min\)
27. largest, \(\displaystyle 786Ω\), smallest, \(\displaystyle 20.32Ω\)
29. 29.6 W
31. a. 0.74 A;
b. 0.742 A
33. a. 60.8 W;
b. 3.18 kW
35. a. \(\displaystyle R_s=9.00Ω\);
b.\(\displaystyle I_1=I_2=I_3=2.00A\);
c. \(\displaystyle V_1=8.00V,V_2=2.00V,V_3=8.00V\);
d. \(\displaystyle P_1=16.00W, P_2=4.00W, P_3=16.00W\);
e. \(\displaystyle P=36.00W\)
37. a. \(\displaystyle I_1=0.6mA, I_2=0.4mA, I_3=0.2m\);
b. \(\displaystyle I_1=0.04mA, I_2=1.52mA, I_3=−1.48mA\);
c. \(\displaystyle P_{out}=0.92mW, P_{out}=4.50mW\);
d. \(\displaystyle P_{in}=0.92mW,P_{in}=4.50mW\)
39. \(\displaystyle V_1=42V,V_2=6V,R_4=18Ω\)
41. a. \(\displaystyle I_1=1.5A,I_2=2A,I_3=0.5A,I_4=2.5A,I_5=2A\);
b. \(\displaystyle P_{in}=I_2V_1+I_5V_5=34W\);
c. \(\displaystyle P_{out}=I^2_1R_1+I^2_2R_2+I^2_3R_3+I^2_4R_4=34W\)
43. \(\displaystyle I_1=\frac{2}{3}\frac{V}{R},I_2=\frac{1}{3}\frac{V}{R},I_3=\frac{1}{3}\frac{V}{R}\)
45. a.
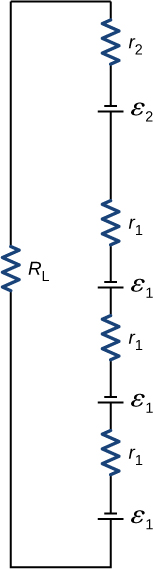
b. 0.617 A;
c. 3.81 W;
d. \(\displaystyle 18.0Ω\)
47. \(\displaystyle I_1r_1−ε_1+I_1R_4+ε_4+I_2r_4+I_4r_3−ε_3+I_2R_3+I_1R_1=0\)
59. 12.0 V
61. 400 V
63. a. 6.00 mV; .
b. It would not be necessary to take extra precautions regarding the power coming from the wall. However, it is possible to generate voltages of approximately this value from static charge built up on gloves, for instance, so some precautions are necessary.
65. a. \(\displaystyle 5.00×10^{−2}C\);
b. 10.0 kV;
c. \(\displaystyle 1.00kΩ\);
d. \(\displaystyle 1.79×10^{−2}°C\)
Challenge Problems
89. a. 0.273 A; b. \(\displaystyle V_T=1.36V\)
91. a. \(\displaystyle V_s=V−I_MR_M=9.99875V\);
b. \(\displaystyle R_S=\frac{V_P}{I_M}=199.975kΩ\)
93. a. \(\displaystyle τ=3800s\);
b. 1.26 A;
c. \(\displaystyle t=2633.96s\)
95. \(\displaystyle R_{eq}=(\sqrt{3}-1)R\)
97. a. \(\displaystyle P_{imheater}=\frac{1cup(\frac{0.000237m^3}{cup})(\frac{1000kg}{m^3})(4186\frac{J}{kg °C})(100°C−20°C)}{180.00s}≈441W\),
b. \(\displaystyle I=\frac{441W}{120V}+4(\frac{100W}{120V})+\frac{1500W}{120V}=19.51A\); Yes, the breaker will trip.
c. \(\displaystyle I=\frac{441W}{120V}+4(\frac{18W}{120V})+\frac{1500W}{120V}=13.47\); No, the breaker will not trip.
99. \(\displaystyle 2.40×10^{−3}Ω\)
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).