7.1: The Angular Momentum of a Point and The Cross Product
- Page ID
- 63163
In the previous section we studied the rotation of extended, rigid objects, arguing that such objects rotate by transfering angular momentum, in a similar way that point-like objects transfer linear momentum. In this section, we start by acknowledging that it's not only extended rigid objects that have angular momentum! Since such objects are made up of individual points, it must be that we can assign angular momentum to the individual points of extended objects. Put another way, it must be possible to determine the angular momentum of a point moving along any path, as shown in the following figure.
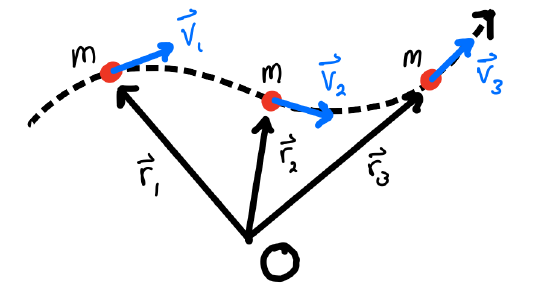
So there must be some way to encode the angular momentum \(\vec{L}\) of this particle as it moves - and in fact, however we define it, if this system is isolated it also had better not change as it moves along this path! It turns out the correct way to do this the following:
\[\vec{L}=\vec{r} \times \vec{p}.\label{eq:PointL}\]
In this expression \(\vec{r}\) is the position of the point, and \(\vec{p}\) is it's momentum. The product here is called the cross product, which we first describe in pure mathematical terms before attempting to understand it physically.
The cross, or vector, product of two vectors \(\vec A\) and \(\vec B\) is denoted by \(\vec{A} \times \vec{B}\). It is defined as a vector perpendicular to both \(\vec A\) and \(\vec B\) (that is to say, to the plane that contains them both), with a magnitude given by
\[ |\vec{A} \times \vec{B}|=A B \sin \theta \label{eq:9.9} \]
where \(A\) and \(B\) are the magnitudes of \(\vec A\) and \(\vec B\), respectively, and \(\theta\) is the angle between \(\vec A\) and \(\vec B\), when they are drawn either with the same origin or tip-to-tail.
Since the result of \(\vec{A} \times \vec{B}\) is a vector, we can also write this product in components. You might recognize this formula from your calculus courses, where you can define it as a determinant (for more information on where this formula comes from, check out Wikipedia). We will just copy the result down here:
\[\vec{A}\times\vec{B}=(A_yB_z-A_zB_y)\hat{x}-(A_xB_z-A_zB_y)\hat{y}+(A_xB_y-A_yB_x)\hat{z}.\label{eq:CrossProduct}\]
Note that the magnitude of the formula we just wrote had better be equivalent to the version above, \(|A||B|\sin(\theta) \). It's not too hard to show that, you just need to relate the components to the angle \(\theta\) by computing (\ref{eq:CrossProduct}) in a particular coordinate system.
The specific direction of \(\vec A \times \vec B\) depends on the relative orientation of the two vectors. Basically, if \(\vec B\) is counterclockwise from \(\vec A\), when looking down on the plane in which they lie, assuming they are drawn with a common origin, then \(\vec{A} \times \vec{B}\) points upwards from that plane; otherwise, it points downward (into the plane). One can also use the so-called right-hand rule, illustrated in Figure \(\PageIndex{1}\) to figure out the direction of \(\vec{A} \times \vec{B}\). Note that, by this definition, the direction of \(\vec{A} \times \vec{B}\) is the opposite of the direction of \(\vec{B} \times \vec{A}\) (as also illustrated in Figure \(\PageIndex{1}\)). Hence, the cross-product is non-commutative: the order of the factors makes a difference.
\[ \vec{A} \times \vec{B}=-\vec{B} \times \vec{A} \label{eq:9.10} \]
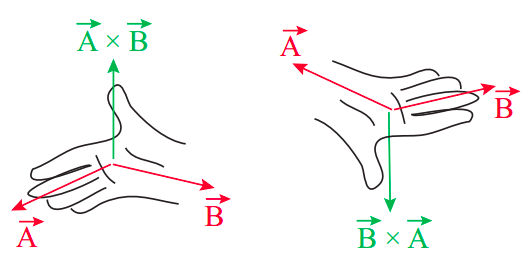
It follows from Equation (\ref{eq:9.10}) that the cross-product of any vector with itself must be zero. In fact, according to Equation (\ref{eq:9.9}), the cross product of any two vectors that are parallel to each other is zero, since in that case \(\theta\) = 0, and \(\sin 0\) = 0.
Besides not being commutative, the cross product also does not have the associative property of ordinary multiplication: \(\vec{A} \times(\vec{B} \times \vec{C}) \) is different from \((\vec{A} \times \vec{B}) \times \vec{C} \). You can see this easily from the fact that, if \(\vec A = \vec B\), the second expression will be zero, but the first one generally will be nonzero (since \(\vec{A} \times \vec{C}\) is not parallel, but rather perpendicular to \(\vec A\)).
Of course, now that we have another definition of the angular momentum, we had better check that it matches the previous one, \(\vec{L}=I\vec{\omega}\). Since that one only applies to rigid objects, let's calculate it for a single particle, and demonstrate that we get the same answer using the equation presented at the beginning of this section, (\ref{eq:PointL}). Consider a particle moving in the \(x-y\) plane, shown in the figure below. Finding the angular momentum of this particle as a rigid object is easy,
\[L=I\omega = (mr^2)\omega.\]
(Recall that the moment of inertia of a single point is the same as for a hoop). Now, let's use our new formula. In the magnitude form (\ref{eq:9.9}), this is
\[L=|r||p|sin\theta=r(mv)sin(90^{\circ}).\]
Here the \(90^{\circ}\) comes from the fact that the vector \(\vec{r}\) and the vector \(\vec{p}\) are perpendicular to each other. To make these expressions match, first notice that \(sin(90^{\circ})=1\). Then, recall the formula \(v=\omega r\) (Equation 6.1.11). If we put both of these into our last expression we find:
\[L=r(mv)sin(90^{\circ})=rm(\omega r)=mr^2\omega,\]
exactly as we expected. For our purposes, this provides enough evidence that we can use (\ref{eq:PointL}) as the correct expression for the angular momentum of single particles.
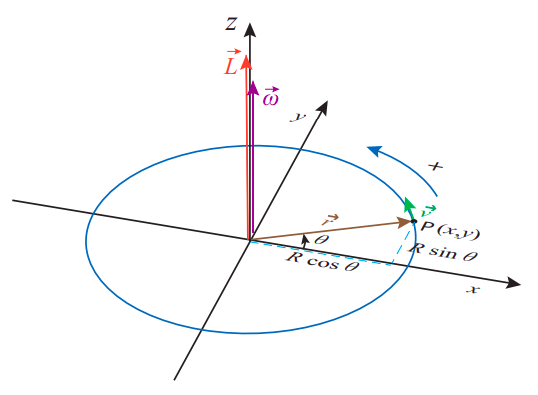
There are some other neat things we can do with \(\vec \omega\) as defined above. Consider the cross product \(\vec{\omega} \times \vec{r}\). Inspection of Figure \(\PageIndex{2}\) and of Equation (8.4.12) shows that this is nothing other than the ordinary velocity vector, \(\vec v\):
\[ \vec{v}=\vec{\omega} \times \vec{r} \label{eq:9.14} .\]
We can also take the derivative of \(\vec \omega\) to obtain the angular acceleration vector \(\vec \alpha\):
\[ \vec{\alpha}=\lim _{\Delta t \rightarrow 0} \frac{\vec{\omega}(t+\Delta t)-\vec{\omega}(t)}{d t}=\frac{d \vec{\omega}}{d t} \label{eq:9.15} .\]
Notice this "new" equation is just another example of the correspondence between angular and linear quantities - the angular acceleration is the derivative of the angular position with respect to time. For the motion depicted in Figure \(\PageIndex{2}\), the vector \(\vec \alpha\) will point along the positive \(z\) axis if the vector \(\vec \omega\) is growing (which means the particle is speeding up), and along the negative \(z\) axis if \(\vec \omega\) is decreasing.
One important property the cross product does have is the distributive property with respect to the sum:
\[ (\vec{A}+\vec{B}) \times \vec{C}=\vec{A} \times \vec{C}+\vec{B} \times \vec{C} \label{eq:9.16} .\]
This, it turns out, is all that’s necessary in order to be able to apply the product rule of differentiation to calculate the derivative of a cross product; you just have to be careful not to change the order of the factors in doing so. We can then take the derivative of both sides of Equation (\ref{eq:9.14}) to get an expression for the acceleration vector:
\begin{align}
\vec{a}=\frac{d \vec{v}}{d t} &=\frac{d \vec{\omega}}{d t} \times \vec{r}+\vec{\omega} \times \frac{d \vec{r}}{d t} \nonumber \\
&=\vec{\alpha} \times \vec{r}+\vec{\omega} \times \vec{v} \label{eq:9.17} .
\end{align}
The first term on the right-hand side, \(\vec{\alpha} \times \vec{r}\), lies in the \(x\)-\(y\) plane, and is perpendicular to \(\vec r\); it is, therefore, tangential to the circle. In fact, looking at its magnitude, it is clear that this is just the tangential acceleration vector.
As for the second term in (\ref{eq:9.17}), \(\vec \omega \times \vec v\), noting that \(\vec \omega\) and \(\vec v\) are always perpendicular, it is clear its magnitude is \(|\omega||\vec{v}|=R \omega^{2}=v^{2} / R\) (making use of Equation (6.1.11) again). This called the centripetal acceleration, which we will explore in more detail when we study rotational motion. Also, using the right-hand rule in Figure \(\PageIndex{2}\), you can see that \(\vec{\omega} \times \vec{v}\) always points inwards, towards the center of the circle; that is, along the direction of \(−\vec r\). Putting all of this together, we can write this vector as just \(−\omega^2 \vec r\), and the whole acceleration vector as the sum of a tangential and a centripetal (radial) component, as follows:
To conclude this section, let me return to the angular momentum vector, and ask the question of whether, in general, the angular momentum of a rotating system, defined as the sum of the angular momentum over all the particles that make up the system, will or not satisfy the vector equation \(\vec L = I\vec{\omega}\). We have seen that this indeed works for a particle moving in a circle. It will, therefore, also work for any object that is essentially flat, and rotating about an axis perpendicular to it, since in that case all its parts are just moving in circles around a common center.
However, if the system is a three-dimensional object rotating about an arbitrary axis, the result \(\vec L = I\vec \omega\) does not generally hold. The reason is, mathematically, that the moment of inertia \(I\) is defined (Equation (6.1.2)) in terms of the distances of the particles to an axis, whereas the angular momentum involves the particle’s distance to a point. For particles at different “heights” along the axis of rotation, these quantities are different. It can be shown that, in the general case, all we can say is that \(L_z = I\omega_z\), if we call \(z\) the axis of rotation and calculate \(\vec L\) relative to a point on that axis.
On the other hand, if the axis of rotation is an axis of symmetry of the object, then \(\vec L\) has only a \(z\) component, and the result \(\vec L = I\vec \omega\) holds as a vector equation. Most of the systems we will consider this semester will be covered under this clause, or under the “essentially flat” clause mentioned above.
In what follows we will generally assume that \(I\) has only a \(z\) component, and we will drop the subscript \(z\) in the equation \(L_z = I\omega_z\), so that \(L\) and \(\omega\) will not necessarily be the magnitudes of their respective vectors, but numbers that could be positive or negative, depending on the direction of rotation (clockwise or counterclockwise). This is essentially the same convention we used for vectors in one dimension, such as \(\vec a\) or \(\vec p\), in the early chapters; it is fine for all the cases in which the (direction of the) axis of rotation does not change with time, which are the only situations we will consider this semester.