3.E: Electric Potential (Exercises)
- Last updated
- Jan 13, 2021
- Save as PDF
- Page ID
- 32170
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
7.2: Electric Potential Energy
1. Would electric potential energy be meaningful if the electric field were not conservative?
2. Why do we need to be careful about work done on the system versus work done by the system in calculations?
3. Does the order in which we assemble a system of point charges affect the total work done?
7.3: Electric Potential and Potential Difference
4. Discuss how potential difference and electric field strength are related. Give an example.
5. What is the strength of the electric field in a region where the electric potential is constant?
6. If a proton is released from rest in an electric field, will it move in the direction of increasing or decreasing potential? Also answer this question for an electron and a neutron. Explain why.
7. Voltage is the common word for potential difference. Which term is more descriptive, voltage or potential difference?
8. If the voltage between two points is zero, can a test charge be moved between them with zero net work being done? Can this necessarily be done without exerting a force? Explain.
9. What is the relationship between voltage and energy? More precisely, what is the relationship between potential difference and electric potential energy?
10. Voltages are always measured between two points. Why?
11. How are units of volts and electron-volts related? How do they differ?
12. Can a particle move in a direction of increasing electric potential, yet have its electric potential energy decrease? Explain
7.4: Calculations of Electric Potential
13. Compare the electric dipole moments of charges ±Q separated by a distance d and charges ±Q/2 separated by a distance d/2.
14. Would Gauss’s law be helpful for determining the electric field of a dipole? Why?
15. In what region of space is the potential due to a uniformly charged sphere the same as that of a point charge? In what region does it differ from that of a point charge?
16. Can the potential of a nonuniformly charged sphere be the same as that of a point charge? Explain.
7.5: Determining Field from Potential
17. If the electric field is zero throughout a region, must the electric potential also be zero in that region?
18. Explain why knowledge of →E(x,y,z) is not sufficient to determine V(x,y,z). What about the other way around?
7.6: Equipotential Surfaces and Conductors
19. If two points are at the same potential, are there any electric field lines connecting them?
20. Suppose you have a map of equipotential surfaces spaced 1.0 V apart. What do the distances between the surfaces in a particular region tell you about the strength of the →E in that region?
21. Is the electric potential necessarily constant over the surface of a conductor?
22. Under electrostatic conditions, the excess charge on a conductor resides on its surface. Does this mean that all of the conduction electrons in a conductor are on the surface?
23. Can a positively charged conductor be at a negative potential? Explain.
24. Can equipotential surfaces intersect?
7.7: Applications of Electrostatics
25. Why are the metal support rods for satellite network dishes generally grounded?
26. (a) Why are fish reasonably safe in an electrical storm?
(b) Why are swimmers nonetheless ordered to get out of the water in the same circumstance?
27. What are the similarities and differences between the processes in a photocopier and an electrostatic precipitator?
28. About what magnitude of potential is used to charge the drum of a photocopy machine? A web search for “xerography” may be of use.
Problems
7.2 Electric Potential Energy
29. Consider a charge Q1(+5.0μC) fixed at a site with another charge Q2 (charge +3.0μC, mass 6.0μg) moving in the neighboring space. (a) Evaluate the potential energy of Q2 when it is 4.0 cm from Q1. (b) If Q2 starts from rest from a point 4.0 cm from Q1, what will be its speed when it is 8.0 cm from Q1? (Note: Q1 is held fixed in its place.)
30. Two charges Q1(+2.00μC) and Q2(+2.00μC) are placed symmetrically along the x-axis at x=±3.00cm. Consider a charge Q3 of charge +4.00μC and mass 10.0 mg moving along the y-axis. If Q3 starts from rest at y=2.00cm, what is its speed when it reaches y=4.00cm?
31. To form a hydrogen atom, a proton is fixed at a point and an electron is brought from far away to a distance of 0.529×10−10m, the average distance between proton and electron in a hydrogen atom. How much work is done?
32. (a) What is the average power output of a heart defibrillator that dissipates 400 J of energy in 10.0 ms? (b) Considering the high-power output, why doesn’t the defibrillator produce serious burns?
7.3 Electric Potential and Potential Difference
33. Find the ratio of speeds of an electron and a negative hydrogen ion (one having an extra electron) accelerated through the same voltage, assuming non-relativistic final speeds. Take the mass of the hydrogen ion to be 1.67×10−27kg.
34. An evacuated tube uses an accelerating voltage of 40 kV to accelerate electrons to hit a copper plate and produce X-rays. Non-relativistically, what would be the maximum speed of these electrons?
35. Show that units of V/m and N/C for electric field strength are indeed equivalent.
36. What is the strength of the electric field between two parallel conducting plates separated by 1.00 cm and having a potential difference (voltage) between them of 1.50×104V?
37. The electric field strength between two parallel conducting plates separated by 4.00 cm is 7.50×104V.
(a) What is the potential difference between the plates?
(b) The plate with the lowest potential is taken to be zero volts. What is the potential 1.00 cm from that plate and 3.00 cm from the other?
38. The voltage across a membrane forming a cell wall is 80.0 mV and the membrane is 9.00 nm thick. What is the electric field strength? (The value is surprisingly large, but correct.) You may assume a uniform electric field.
39. Two parallel conducting plates are separated by 10.0 cm, and one of them is taken to be at zero volts.
(a) What is the electric field strength between them, if the potential 8.00 cm from the zero volt plate (and 2.00 cm from the other) is 450 V?
(b) What is the voltage between the plates?
40. Find the maximum potential difference between two parallel conducting plates separated by 0.500 cm of air, given the maximum sustainable electric field strength in air to be 3.0×106V/m.
41. An electron is to be accelerated in a uniform electric field having a strength of 2.00×106V/m.
(a) What energy in keV is given to the electron if it is accelerated through 0.400 m?
(b) Over what distance would it have to be accelerated to increase its energy by 50.0 GeV?
42. Use the definition of potential difference in terms of electric field to deduce the formula for potential difference between r=ra and r=rb for a point charge located at the origin. Here r is the spherical radial coordinate.
43. The electric field in a region is pointed away from the z-axis and the magnitude depends upon the distance s from the axis. The magnitude of the electric field is given as E=αs where α is a constant. Find the potential difference between points P1 and P2, explicitly stating the path over which you conduct the integration for the line integral.
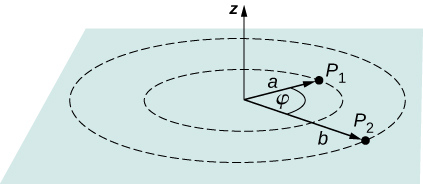
44. Singly charged gas ions are accelerated from rest through a voltage of 13.0 V. At what temperature will the average kinetic energy of gas molecules be the same as that given these ions?
7.4 Calculations of Electric Potential
45. A 0.500-cm-diameter plastic sphere, used in a static electricity demonstration, has a uniformly distributed 40.0-pC charge on its surface. What is the potential near its surface?
46. How far from a 1.00−μC point charge is the potential 100 V? At what distance is it 2.00×102V?
47. If the potential due to a point charge is 5.00×102V at a distance of 15.0 m, what are the sign and magnitude of the charge?
48. In nuclear fission, a nucleus splits roughly in half. (a) What is the potential 2.00×10−14m from a fragment that has 46 protons in it? (b) What is the potential energy in MeV of a similarly charged fragment at this distance?
49. A research Van de Graaff generator has a 2.00-m-diameter metal sphere with a charge of 5.00 mC on it. Assume the potential energy is zero at a reference point infinitely far away from the Van de Graaff.
(a) What is the potential near its surface?
(b) At what distance from its center is the potential 1.00 MV?
(c) An oxygen atom with three missing electrons is released near the Van de Graaff generator. What is its kinetic energy in MeV when the atom is at the distance found in part b?
50. An electrostatic paint sprayer has a 0.200-m-diameter metal sphere at a potential of 25.0 kV that repels paint droplets onto a grounded object.
(a) What charge is on the sphere?
(b) What charge must a 0.100-mg drop of paint have to arrive at the object with a speed of 10.0 m/s?
51. (a) What is the potential between two points situated 10 cm and 20 cm from a 3.0−μC point charge?
(b) To what location should the point at 20 cm be moved to increase this potential difference by a factor of two?
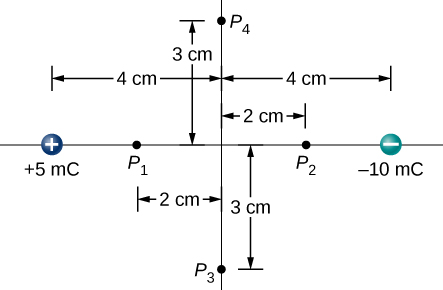
52. Find the potential at points P1,P2,P3, and P4 in the diagram due to the two given charges.
53. Two charges –2.0µC and +2.0µC are separated by 4.0 cm on the z-axis symmetrically about origin, with the positive one uppermost. Two space points of interest P1 and P2 are located 3.0 cm and 30 cm from origin at an angle 30° with respect to the z-axis. Evaluate electric potentials at P1 and P2 in two ways:
(a) Using the exact formula for point charges, and
(b) using the approximate dipole potential formula.
54. (a) Plot the potential of a uniformly charged 1-m rod with 1 C/m charge as a function of the perpendicular distance from the center. Draw your graph from s=0.1m to s=1.0m.
(b) On the same graph, plot the potential of a point charge with a 1-C charge at the origin.
(c) Which potential is stronger near the rod? (d) What happens to the difference as the distance increases? Interpret your result.
7.5 Determining Field from Potential
55. Throughout a region, equipotential surfaces are given by z=constant. The surfaces are equally spaced with V=100V for z=0.00m,V=200V for z=0.50m,V=300V for z=1.00m. What is the electric field in this region?
56. In a particular region, the electric potential is given by V=−xy2z+4xy. What is the electric field in this region?
57. Calculate the electric field of an infinite line charge, throughout space.
7.6 Equipotential Surfaces and Conductors
58. Two very large metal plates are placed 2.0 cm apart, with a potential difference of 12 V between them. Consider one plate to be at 12 V, and the other at 0 V. (a) Sketch the equipotential surfaces for 0, 4, 8, and 12 V.
(b) Next sketch in some electric field lines, and confirm that they are perpendicular to the equipotential lines.
59. A very large sheet of insulating material has had an excess of electrons placed on it to a surface charge density of –3.00nC/m2.
(a) As the distance from the sheet increases, does the potential increase or decrease? Can you explain why without any calculations? Does the location of your reference point matter?
(b) What is the shape of the equipotential surfaces?
(c) What is the spacing between surfaces that differ by 1.00 V?
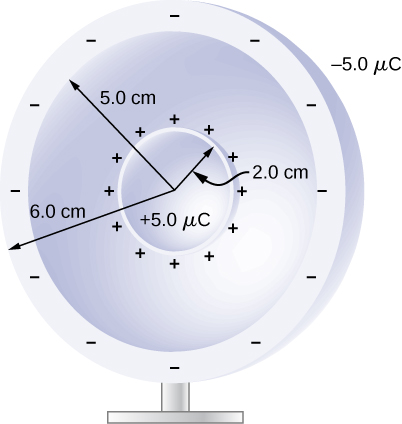
60. A metallic sphere of radius 2.0 cm is charged with +5.0−μC charge, which spreads on the surface of the sphere uniformly. The metallic sphere stands on an insulated stand and is surrounded by a larger metallic spherical shell, of inner radius 5.0 cm and outer radius 6.0 cm. Now, a charge of −5.0−μC is placed on the inside of the spherical shell, which spreads out uniformly on the inside surface of the shell. If potential is zero at infinity, what is the potential of
(a) the spherical shell,
(b) the sphere,
(c) the space between the two,
(d) inside the sphere, and
(e) outside the shell?
61. Two large charged plates of charge density ±30μC/m2 face each other at a separation of 5.0 mm.
(a) Find the electric potential everywhere.
(b) An electron is released from rest at the negative plate; with what speed will it strike the positive plate?
62. A long cylinder of aluminum of radius R meters is charged so that it has a uniform charge per unit length on its surface of λ.
(a) Find the electric field inside and outside the cylinder.
(b) Find the electric potential inside and outside the cylinder. (c) Plot electric field and electric potential as a function of distance from the center of the rod.
63. Two parallel plates 10 cm on a side are given equal and opposite charges of magnitude 5.0×10−9C.The plates are 1.5 mm apart. What is the potential difference between the plates?
64. The surface charge density on a long straight metallic pipe is σ. What is the electric potential outside and inside the pipe? Assume the pipe has a diameter of 2a.

65. Concentric conducting spherical shells carry charges Q and –Q, respectively. The inner shell has negligible thickness. What is the potential difference between the shells?
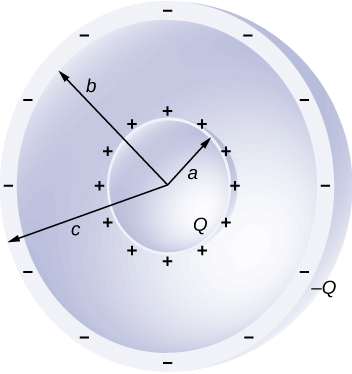
66. Shown below are two concentric spherical shells of negligible thicknesses and radii R1 and R2. The inner and outer shell carry net charges q1 and q2, respectively, where both q1 and q2 are positive. What is the electric potential in the regions (a) r<R1, (b) R1<r<R2, and (c) r>R2?
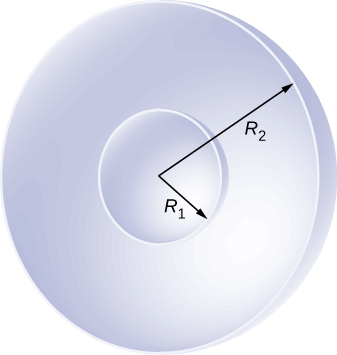
67. A solid cylindrical conductor of radius a is surrounded by a concentric cylindrical shell of inner radius b. The solid cylinder and the shell carry charges Q and –Q, respectively. Assuming that the length L of both conductors is much greater than a or b, what is the potential difference between the two conductors?
7.7 Applications of Electrostatics
68. (a) What is the electric field 5.00 m from the center of the terminal of a Van de Graaff with a 3.00-mC charge, noting that the field is equivalent to that of a point charge at the center of the terminal?
(b) At this distance, what force does the field exert on a 2.00−μC charge on the Van de Graaff’s belt?
69. (a) What is the direction and magnitude of an electric field that supports the weight of a free electron near the surface of Earth?
(b) Discuss what the small value for this field implies regarding the relative strength of the gravitational and electrostatic forces.
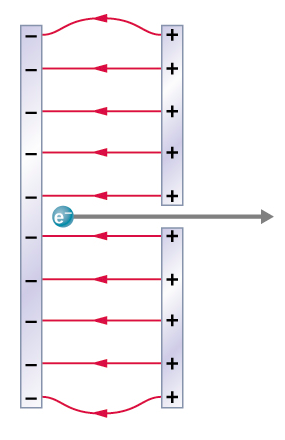
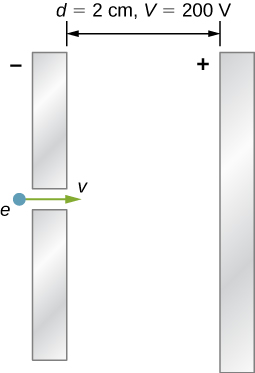
70. A simple and common technique for accelerating electrons is shown in Figure 3.E.1, where there is a uniform electric field between two plates. Electrons are released, usually from a hot filament, near the negative plate, and there is a small hole in the positive plate that allows the electrons to continue moving.
(a) Calculate the acceleration of the electron if the field strength is 2.50×104N/C.
(b) Explain why the electron will not be pulled back to the positive plate once it moves through the hole.
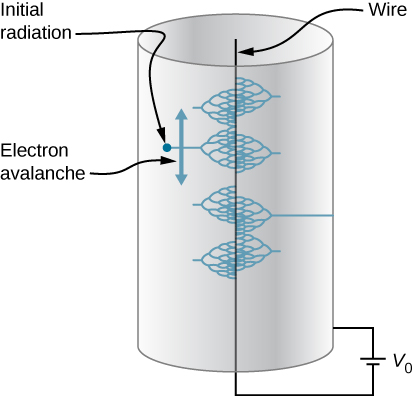
71. In a Geiger counter, a thin metallic wire at the center of a metallic tube is kept at a high voltage with respect to the metal tube. Ionizing radiation entering the tube knocks electrons off gas molecules or sides of the tube that then accelerate towards the center wire, knocking off even more electrons. This process eventually leads to an avalanche that is detectable as a current. A particular Geiger counter has a tube of radius R and the inner wire of radius a is at a potential of V0 volts with respect to the outer metal tube. Consider a point P at a distance s from the center wire and far away from the ends.
(a) Find a formula for the electric field at a point P inside using the infinite wire approximation.
(b) Find a formula for the electric potential at a point P inside.
(c) Use V0=900V,a=3.00mm,R=2.00cm, and find the value of the electric field at a point 1.00 cm from the center.
72. The practical limit to an electric field in air is about 3.00×106N/C. Above this strength, sparking takes place because air begins to ionize.
(a) At this electric field strength, how far would a proton travel before hitting the speed of light (ignore relativistic effects)?
(b) Is it practical to leave air in particle accelerators?
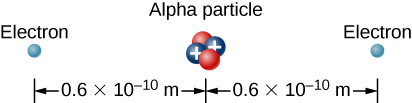
73. To form a helium atom, an alpha particle that contains two protons and two neutrons is fixed at one location, and two electrons are brought in from far away, one at a time. The first electron is placed at 0.600×10−10m from the alpha particle and held there while the second electron is brought to 0.600×10−10m from the alpha particle on the other side from the first electron. See the final configuration below.
(a) How much work is done in each step?
(b) What is the electrostatic energy of the alpha particle and two electrons in the final configuration?
74. Find the electrostatic energy of eight equal charges (+3µC) each fixed at the corners of a cube of side 2 cm.
75. The probability of fusion occurring is greatly enhanced when appropriate nuclei are brought close together, but mutual Coulomb repulsion must be overcome. This can be done using the kinetic energy of high-temperature gas ions or by accelerating the nuclei toward one another.
(a) Calculate the potential energy of two singly charged nuclei separated by 1.00×10−12m.
(b) At what temperature will atoms of a gas have an average kinetic energy equal to this needed electrical potential energy?
76. A bare helium nucleus has two positive charges and a mass of 6.64×10–27kg.
(a) Calculate its kinetic energy in joules at 2.00 of the speed of light.
(b) What is this in electron-volts?
(c) What voltage would be needed to obtain this energy?
77. An electron enters a region between two large parallel plates made of aluminum separated by a distance of 2.0 cm and kept at a potential difference of 200 V. The electron enters through a small hole in the negative plate and moves toward the positive plate. At the time the electron is near the negative plate, its speed is 4.0×105m/s. Assume the electric field between the plates to be uniform, and find the speed of electron at
(a) 0.10 cm,
(b) 0.50 cm,
(c) 1.0 cm, and
(d) 1.5 cm from the negative plate, and
(e) immediately before it hits the positive plate.
78. How far apart are two conducting plates that have an electric field strength of 4.50×103V/m between them, if their potential difference is 15.0 kV?
79. (a) Will the electric field strength between two parallel conducting plates exceed the breakdown strength of dry air, which is 3.00×106V/m, if the plates are separated by 2.00 mm and a potential difference of 5.0×103V is applied?
(b) How close together can the plates be with this applied voltage?
80. Membrane walls of living cells have surprisingly large electric fields across them due to separation of ions. What is the voltage across an 8.00-nm-thick membrane if the electric field strength across it is 5.50 MV/m? You may assume a uniform electric field.
81. A double charged ion is accelerated to an energy of 32.0 keV by the electric field between two parallel conducting plates separated by 2.00 cm. What is the electric field strength between the plates?
82. The temperature near the center of the Sun is thought to be 15 million degrees Celsius (1.5×107°C) (or kelvin). Through what voltage must a singly charged ion be accelerated to have the same energy as the average kinetic energy of ions at this temperature?
83. A lightning bolt strikes a tree, moving 20.0 C of charge through a potential difference of 1.00×102MV.
(a) What energy was dissipated?
(b) What mass of water could be raised from 15°C to the boiling point and then boiled by this energy?
(c) Discuss the damage that could be caused to the tree by the expansion of the boiling steam.
84. What is the potential 0.530×10−10m from a proton (the average distance between the proton and electron in a hydrogen atom)?
85. (a) A sphere has a surface uniformly charged with 1.00 C. At what distance from its center is the potential 5.00 MV? (b) What does your answer imply about the practical aspect of isolating such a large charge?
86. What are the sign and magnitude of a point charge that produces a potential of –2.00 V at a distance of 1.00 mm?
87. In one of the classic nuclear physics experiments at the beginning of the twentieth century, an alpha particle was accelerated toward a gold nucleus, and its path was substantially deflected by the Coulomb interaction. If the energy of the doubly charged alpha nucleus was 5.00 MeV, how close to the gold nucleus (79 protons) could it come before being deflected?
Additional Problems
88. A 12.0-V battery-operated bottle warmer heats 50.0 g of glass, 2.50×102g of baby formula, and 2.00×102g of aluminum from 20.0°C to 90.0°C.
(a) How much charge is moved by the battery?
(b) How many electrons per second flow if it takes 5.00 min to warm the formula? (Hint: Assume that the specific heat of baby formula is about the same as the specific heat of water.)
89. A battery-operated car uses a 12.0-V system. Find the charge the batteries must be able to move in order to accelerate the 750 kg car from rest to 25.0 m/s, make it climb a 2.00×102−m high hill, and finally cause it to travel at a constant 25.0 m/s while climbing with 5.00×102−N force for an hour.
90. (a) Find the voltage near a 10.0 cm diameter metal sphere that has 8.00 C of excess positive charge on it.
(b) What is unreasonable about this result?
(c) Which assumptions are responsible?
91. A uniformly charged half-ring of radius 10 cm is placed on a nonconducting table. It is found that 3.0 cm above the center of the half-ring the potential is –3.0 V with respect to zero potential at infinity. How much charge is in the half-ring?
92. A glass ring of radius 5.0 cm is painted with a charged paint such that the charge density around the ring varies continuously given by the following function of the polar angle θ,λ=(3.0×10−6C/m)cos2θ.. Find the potential at a point 15 cm above the center.
93. A CD disk of radius (R=3.0cm) is sprayed with a charged paint so that the charge varies continually with radial distance rfrom the center in the following manner: σ=−(6.0C/m)r/R. Find the potential at a point 4 cm above the center.
94. (a) What is the final speed of an electron accelerated from rest through a voltage of 25.0 MV by a negatively charged Van de Graff terminal? (b) What is unreasonable about this result? (c) Which assumptions are responsible?
95. A large metal plate is charged uniformly to a density of σ=2.0×10−9C/m2. How far apart are the equipotential surfaces that represent a potential difference of 25 V?
96. Your friend gets really excited by the idea of making a lightning rod or maybe just a sparking toy by connecting two spheres as shown in Figure 7.39, and making R2 so small that the electric field is greater than the dielectric strength of air, just from the usual 150 V/m electric field near the surface of the Earth. If R1 is 10 cm, how small does R2 need to be, and does this seem practical? (Hint: recall the calculation for electric field at the surface of a conductor from Gauss’s Law.)
97. (a) Find x>>L limit of the potential of a finite uniformly charged rod and show that it coincides with that of a point charge formula. (b) Why would you expect this result?
98. A small spherical pith ball of radius 0.50 cm is painted with a silver paint and then −10μC of charge is placed on it. The charged pith ball is put at the center of a gold spherical shell of inner radius 2.0 cm and outer radius 2.2 cm.
(a) Find the electric potential of the gold shell with respect to zero potential at infinity.
(b) How much charge should you put on the gold shell if you want to make its potential 100 V?
99. Two parallel conducting plates, each of cross-sectional area 400cm2, are 2.0 cm apart and uncharged. If 1.0×1012 electrons are transferred from one plate to the other,
(a) what is the potential difference between the plates?
(b) What is the potential difference between the positive plate and a point 1.25 cm from it that is between the plates?
100. A point charge of q=5.0×10−8C is placed at the center of an uncharged spherical conducting shell of inner radius 6.0 cm and outer radius 9.0 cm. Find the electric potential at
(a) r=4.0cm,
(b) r=8.0cm,
(c) r=12.0cm.
101. Earth has a net charge that produces an electric field of approximately 150 N/C downward at its surface.
(a) What is the magnitude and sign of the excess charge, noting the electric field of a conducting sphere is equivalent to a point charge at its center?
(b) What acceleration will the field produce on a free electron near Earth’s surface?
(c) What mass object with a single extra electron will have its weight supported by this field?
102. Point charges of 25.0μC and 45.0μC are placed 0.500 m apart.
(a) At what point along the line between them is the electric field zero?
(b) What is the electric field halfway between them?
103. What can you say about two charges q1 and q2, if the electric field one-fourth of the way from q1 to q2 is zero?
104. Calculate the angular velocity ω of an electron orbiting a proton in the hydrogen atom, given the radius of the orbit is 0.530×10−10m. You may assume that the proton is stationary and the centripetal force is supplied by Coulomb attraction.
105. An electron has an initial velocity of 5.00×106m/s in a uniform 2.00×105−N/C electric field. The field accelerates the electron in the direction opposite to its initial velocity.
(a) What is the direction of the electric field?
(b) How far does the electron travel before coming to rest?
(c) How long does it take the electron to come to rest?
(d) What is the electron’s velocity when it returns to its starting point?
Challenge Problems
106. Three Na+ and three Cl− ions are placed alternately and equally spaced around a circle of radius 50 nm. Find the electrostatic energy stored.
107. Look up (presumably online, or by dismantling an old device and making measurements) the magnitude of the potential deflection plates (and the space between them) in an ink jet printer. Then look up the speed with which the ink comes out the nozzle. Can you calculate the typical mass of an ink drop?
108. Use the electric field of a finite sphere with constant volume charge density to calculate the electric potential, throughout space. Then check your results by calculating the electric field from the potential.
109. Calculate the electric field of a dipole throughout space from the potential.


