3.9: The Electric Potential (Exercises)
- Page ID
- 100341
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
Electric Potential Energy
1. Would electric potential energy be meaningful if the electric field were not conservative?
2. Why do we need to be careful about work done on the system versus work done by the system in calculations?
3. Does the order in which we assemble a system of point charges affect the total work done?
Electric Potential Energy
Electric Potential Energy of Point Charges
Electric Potential
Electric Potential of a Point Charge
4. Discuss how potential difference and electric field strength are related. Give an example.
5. What is the strength of the electric field in a region where the electric potential is constant?
6. If a proton is released from rest in an electric field, will it move in the direction of increasing or decreasing potential? Also answer this question for an electron and a neutron. Explain why.
7. Voltage is the common word for potential difference. Which term is more descriptive, voltage or potential difference?
8. If the voltage between two points is zero, can a test charge be moved between them with zero net work being done? Can this necessarily be done without exerting a force? Explain.
9. What is the relationship between voltage and energy? More precisely, what is the relationship between potential difference and electric potential energy?
10. Voltages are always measured between two points. Why?
11. How are units of volts and electron-volts related? How do they differ?
12. Can a particle move in a direction of increasing electric potential, yet have its electric potential energy decrease? Explain
Problems
Electric Potential Energy
Electric Potential Energy of Point Charges
29. Consider a charge \(\displaystyle Q_1(+5.0μC)\) fixed at a site with another charge \(\displaystyle Q_2\) (charge \(\displaystyle +3.0μC\), mass \(\displaystyle 6.0μg\)) moving in the neighboring space. (a) Evaluate the potential energy of \(\displaystyle Q_2\) when it is 4.0 cm from \(\displaystyle Q_1\). (b) If \(\displaystyle Q_2\) starts from rest from a point 4.0 cm from \(\displaystyle Q_1\), what will be its speed when it is 8.0 cm from \(\displaystyle Q_1\)? (Note: \(\displaystyle Q_1\) is held fixed in its place.)
30. Two charges \(\displaystyle Q_1(+2.00μC)\) and \(\displaystyle Q_2(+2.00μC)\) are placed symmetrically along the x-axis at \(\displaystyle x=±3.00cm\). Consider a charge \(\displaystyle Q_3\) of charge \(\displaystyle +4.00μC\) and mass 10.0 mg moving along the y-axis. If \(\displaystyle Q_3\) starts from rest at \(\displaystyle y=2.00cm\), what is its speed when it reaches \(\displaystyle y=4.00cm\)?
31. To form a hydrogen atom, a proton is fixed at a point and an electron is brought from far away to a distance of \(\displaystyle 0.529×10^{−10}m\), the average distance between proton and electron in a hydrogen atom. How much work is done?
32. (a) What is the average power output of a heart defibrillator that dissipates 400 J of energy in 10.0 ms? (b) Considering the high-power output, why doesn’t the defibrillator produce serious burns?
Electric Potential
Electric Potential of a Point Charge
33. Find the ratio of speeds of an electron and a negative hydrogen ion (one having an extra electron) accelerated through the same voltage, assuming non-relativistic final speeds. Take the mass of the hydrogen ion to be \(\displaystyle 1.67×10^{−27}kg\).
34. An evacuated tube uses an accelerating voltage of 40 kV to accelerate electrons to hit a copper plate and produce X-rays. Non-relativistically, what would be the maximum speed of these electrons?
35. Show that units of V/m and N/C for electric field strength are indeed equivalent.
36. What is the strength of the electric field between two parallel conducting plates separated by 1.00 cm and having a potential difference (voltage) between them of \(\displaystyle 1.50×10^4V\)?
37. The electric field strength between two parallel conducting plates separated by 4.00 cm is \(\displaystyle 7.50×10^4V\).
(a) What is the potential difference between the plates?
(b) The plate with the lowest potential is taken to be zero volts. What is the potential 1.00 cm from that plate and 3.00 cm from the other?
38. The voltage across a membrane forming a cell wall is 80.0 mV and the membrane is 9.00 nm thick. What is the electric field strength? (The value is surprisingly large, but correct.) You may assume a uniform electric field.
39. Two parallel conducting plates are separated by 10.0 cm, and one of them is taken to be at zero volts.
(a) What is the electric field strength between them, if the potential 8.00 cm from the zero volt plate (and 2.00 cm from the other) is 450 V?
(b) What is the voltage between the plates?
40. Find the maximum potential difference between two parallel conducting plates separated by 0.500 cm of air, given the maximum sustainable electric field strength in air to be \(\displaystyle 3.0×10^6V/m\).
41. An electron is to be accelerated in a uniform electric field having a strength of \(\displaystyle 2.00×10^6V/m\).
(a) What energy in keV is given to the electron if it is accelerated through 0.400 m?
(b) Over what distance would it have to be accelerated to increase its energy by 50.0 GeV?
42. Use the definition of potential difference in terms of electric field to deduce the formula for potential difference between \(\displaystyle r=r_a\) and \(\displaystyle r=r_b\) for a point charge located at the origin. Here r is the spherical radial coordinate.
43. The electric field in a region is pointed away from the z-axis and the magnitude depends upon the distance \(\displaystyle s\) from the axis. The magnitude of the electric field is given as \(\displaystyle E=\frac{α}{s}\) where \(\displaystyle α\) is a constant. Find the potential difference between points \(\displaystyle P_1\) and \(\displaystyle P_2\), explicitly stating the path over which you conduct the integration for the line integral.
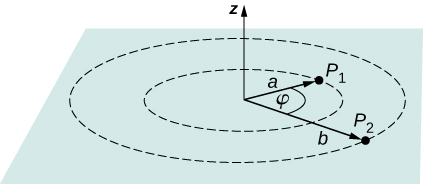
44. Singly charged gas ions are accelerated from rest through a voltage of 13.0 V. At what temperature will the average kinetic energy of gas molecules be the same as that given these ions?
Common Models of Electric Potential
45. A 0.500-cm-diameter plastic sphere, used in a static electricity demonstration, has a uniformly distributed 40.0-pC charge on its surface. What is the potential near its surface?
46. How far from a \(\displaystyle 1.00-μC\) point charge is the potential 100 V? At what distance is it \(\displaystyle 2.00×10^2V\)?
47. If the potential due to a point charge is \(\displaystyle 5.00×10^2V\) at a distance of 15.0 m, what are the sign and magnitude of the charge?
48. In nuclear fission, a nucleus splits roughly in half. (a) What is the potential \(\displaystyle 2.00×10^{−14}m\) from a fragment that has 46 protons in it? (b) What is the potential energy in MeV of a similarly charged fragment at this distance?
49. A research Van de Graaff generator has a 2.00-m-diameter metal sphere with a charge of 5.00 mC on it. Assume the potential energy is zero at a reference point infinitely far away from the Van de Graaff.
(a) What is the potential near its surface?
(b) At what distance from its center is the potential 1.00 MV?
(c) An oxygen atom with three missing electrons is released near the Van de Graaff generator. What is its kinetic energy in MeV when the atom is at the distance found in part b?
50. An electrostatic paint sprayer has a 0.200-m-diameter metal sphere at a potential of 25.0 kV that repels paint droplets onto a grounded object.
(a) What charge is on the sphere?
(b) What charge must a 0.100-mg drop of paint have to arrive at the object with a speed of 10.0 m/s?
51. (a) What is the potential between two points situated 10 cm and 20 cm from a \(\displaystyle 3.0-μC\) point charge?
(b) To what location should the point at 20 cm be moved to increase this potential difference by a factor of two?
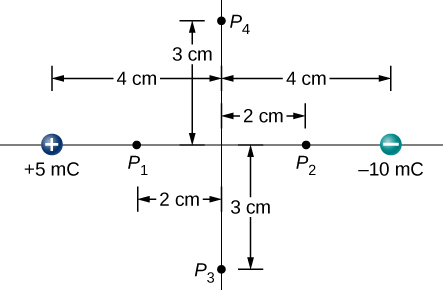
52. Find the potential at points \(\displaystyle P_1, P_2, P_3\), and \(\displaystyle P_4\) in the diagram due to the two given charges.
53. Two charges \(\displaystyle –2.0µC\) and \(\displaystyle +2.0µC\) are separated by 4.0 cm on the z-axis symmetrically about origin, with the positive one uppermost. Two space points of interest \(\displaystyle P_1\) and \(\displaystyle P_2\) are located 3.0 cm and 30 cm from origin at an angle 30° with respect to the z-axis. Evaluate electric potentials at \(\displaystyle P_1\) and \(\displaystyle P_2\) in two ways:
(a) Using the exact formula for point charges, and
(b) using the approximate dipole potential formula.
54. (a) Plot the potential of a uniformly charged 1-m rod with 1 C/m charge as a function of the perpendicular distance from the center. Draw your graph from \(\displaystyle s=0.1m\) to \(\displaystyle s=1.0m\).
(b) On the same graph, plot the potential of a point charge with a 1-C charge at the origin.
(c) Which potential is stronger near the rod? (d) What happens to the difference as the distance increases? Interpret your result.
Additional Problems
88. A 12.0-V battery-operated bottle warmer heats 50.0 g of glass, \(\displaystyle 2.50×10^2g\) of baby formula, and \(\displaystyle 2.00×10^2g\) of aluminum from 20.0°C to 90.0°C.
(a) How much charge is moved by the battery?
(b) How many electrons per second flow if it takes 5.00 min to warm the formula? (Hint: Assume that the specific heat of baby formula is about the same as the specific heat of water.)
89. A battery-operated car uses a 12.0-V system. Find the charge the batteries must be able to move in order to accelerate the 750 kg car from rest to 25.0 m/s, make it climb a \(\displaystyle 2.00×10^2-m\) high hill, and finally cause it to travel at a constant 25.0 m/s while climbing with \(\displaystyle 5.00×10^2-N\) force for an hour.
90. (a) Find the voltage near a 10.0 cm diameter metal sphere that has 8.00 C of excess positive charge on it.
(b) What is unreasonable about this result?
(c) Which assumptions are responsible?
91. A uniformly charged half-ring of radius 10 cm is placed on a nonconducting table. It is found that 3.0 cm above the center of the half-ring the potential is –3.0 V with respect to zero potential at infinity. How much charge is in the half-ring?
92. A glass ring of radius 5.0 cm is painted with a charged paint such that the charge density around the ring varies continuously given by the following function of the polar angle \(\displaystyle θ,λ=(3.0×10^{−6}C/m)cos^2θ.\). Find the potential at a point 15 cm above the center.
93. A CD disk of radius (\(\displaystyle R=3.0cm\)) is sprayed with a charged paint so that the charge varies continually with radial distance rfrom the center in the following manner: \(\displaystyle σ=−(6.0C/m)r/R\). Find the potential at a point 4 cm above the center.
94. (a) What is the final speed of an electron accelerated from rest through a voltage of 25.0 MV by a negatively charged Van de Graff terminal? (b) What is unreasonable about this result? (c) Which assumptions are responsible?
95. A large metal plate is charged uniformly to a density of \(\displaystyle σ=2.0×10^{−9}C/m^2\). How far apart are the equipotential surfaces that represent a potential difference of 25 V?
96. Your friend gets really excited by the idea of making a lightning rod or maybe just a sparking toy by connecting two spheres as shown in Figure 7.39, and making \(\displaystyle R_2\) so small that the electric field is greater than the dielectric strength of air, just from the usual 150 V/m electric field near the surface of the Earth. If \(\displaystyle R_1\) is 10 cm, how small does \(\displaystyle R_2\) need to be, and does this seem practical? (Hint: recall the calculation for electric field at the surface of a conductor from Gauss’s Law.)
97. (a) Find \(\displaystyle x>>L\) limit of the potential of a finite uniformly charged rod and show that it coincides with that of a point charge formula. (b) Why would you expect this result?
98. A small spherical pith ball of radius 0.50 cm is painted with a silver paint and then \(\displaystyle −10μC\) of charge is placed on it. The charged pith ball is put at the center of a gold spherical shell of inner radius 2.0 cm and outer radius 2.2 cm.
(a) Find the electric potential of the gold shell with respect to zero potential at infinity.
(b) How much charge should you put on the gold shell if you want to make its potential 100 V?
99. Two parallel conducting plates, each of cross-sectional area \(\displaystyle 400cm^2\), are 2.0 cm apart and uncharged. If \(\displaystyle 1.0×10^{12}\) electrons are transferred from one plate to the other,
(a) what is the potential difference between the plates?
(b) What is the potential difference between the positive plate and a point 1.25 cm from it that is between the plates?
100. A point charge of \(\displaystyle q=5.0×10^{−8}C\) is placed at the center of an uncharged spherical conducting shell of inner radius 6.0 cm and outer radius 9.0 cm. Find the electric potential at
(a) \(\displaystyle r=4.0cm,\)
(b) \(\displaystyle r=8.0cm,\)
(c) \(\displaystyle r=12.0cm\).
101. Earth has a net charge that produces an electric field of approximately 150 N/C downward at its surface.
(a) What is the magnitude and sign of the excess charge, noting the electric field of a conducting sphere is equivalent to a point charge at its center?
(b) What acceleration will the field produce on a free electron near Earth’s surface?
(c) What mass object with a single extra electron will have its weight supported by this field?
102. Point charges of \(\displaystyle 25.0μC\) and \(\displaystyle 45.0μC\) are placed 0.500 m apart.
(a) At what point along the line between them is the electric field zero?
(b) What is the electric field halfway between them?
103. What can you say about two charges \(\displaystyle q_1\) and \(\displaystyle q_2\), if the electric field one-fourth of the way from \(\displaystyle q_1\) to \(\displaystyle q_2\) is zero?
104. Calculate the angular velocity \(\displaystyle ω\) of an electron orbiting a proton in the hydrogen atom, given the radius of the orbit is \(\displaystyle 0.530×10^{−10}m\). You may assume that the proton is stationary and the centripetal force is supplied by Coulomb attraction.
105. An electron has an initial velocity of \(\displaystyle 5.00×10^6m/s\) in a uniform \(\displaystyle 2.00×10^5-N/C\) electric field. The field accelerates the electron in the direction opposite to its initial velocity.
(a) What is the direction of the electric field?
(b) How far does the electron travel before coming to rest?
(c) How long does it take the electron to come to rest?
(d) What is the electron’s velocity when it returns to its starting point?
Challenge Problems
106. Three \(\displaystyle Na^+\) and three \(\displaystyle Cl^−\) ions are placed alternately and equally spaced around a circle of radius 50 nm. Find the electrostatic energy stored.
107. Look up (presumably online, or by dismantling an old device and making measurements) the magnitude of the potential deflection plates (and the space between them) in an ink jet printer. Then look up the speed with which the ink comes out the nozzle. Can you calculate the typical mass of an ink drop?
108. Use the electric field of a finite sphere with constant volume charge density to calculate the electric potential, throughout space. Then check your results by calculating the electric field from the potential.
109. Calculate the electric field of a dipole throughout space from the potential.
Contributors and Attributions
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).