5.1: Introduction to UCM and Gravitation
- Last updated
- Jan 14, 2019
- Save as PDF
- Page ID
- 16947

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Kinematics of UCM
Uniform circular motion is a motion in a circular path at constant speed.
learning objectives
- Relate centripetal force and centripetal acceleration to uniform circular motion
Angular Quantities
Under uniform circular motion, angular and linear quantities have simple relations. When objects rotate about some axis, each point in the object follows a circular arc. The rotation angle is the amount of rotation and is analogous to linear distance. We define the rotation angle Δθ to be the ratio of the arc length to the radius of curvature:
Δθ=Δsr
Angle θθ and Arc Length ss: The radius of a circle is rotated through an angle Δθ. The arc length Δs is described on the circumference.
We define angular velocity ωω as the rate of change of an angle. In symbols, this is ω=ΔθΔt, where an angular rotation Δθ takes place in a time Δt. From the relation of s and (Δs=rΔθ), we see:
v=ΔsΔt=rΔθΔt=rω
Under uniform circular motion, the angular velocity is constant. The acceleration can be written as:
ac=dvdt=ωdrdt=ωv=rω2=v2r
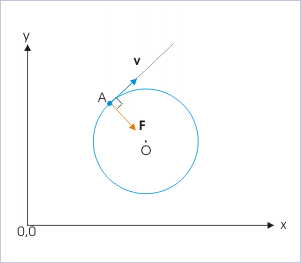
This acceleration, responsible for the uniform circular motion, is called centripetal acceleration.
Centripetal Force
Any force or combination of forces can cause a centripetal or radial acceleration. Just a few examples are the tension in the rope on a tether ball, the force of Earth’s gravity on the Moon, friction between roller skates and a rink floor, a banked roadway’s force on a car, and forces on the tube of a spinning centrifuge.
Any net force causing uniform circular motion is called a centripetal force. The direction of a centripetal force is toward the center of curvature, the same as the direction of centripetal acceleration. According to Newton’s second law of motion, net force is mass times acceleration. For uniform circular motion, the acceleration is the centripetal acceleration: a=ac. Thus, the magnitude of centripetal force Fc is:
Fc=mac=mv2r=mrω2
Dynamics of UCM
Newton’s universal law of gravitation states that every particle attracts every other particle with a force along a line joining them.
learning objectives
- Relate Kepler’s laws to Newton’s universal law of gravitation
Newton’s Universal Law of Gravitation
Newton’s universal law of gravitation states that every particle in the universe attracts every other particle with a force along a line joining them. The force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. For two bodies having masses mm and MM with a distance rr between their centers of mass, the equation for Newton’s universal law of gravitation is:
F=GmMr2
The gravitational force is responsible for artificial satellites orbiting the Earth. The Moon’s orbit about Earth, the orbits of planets, asteroids, meteors, and comets about the Sun are other examples of gravitational orbits. Historically, Kepler discovered his 3 laws (called Kepler’s law of planetary motion) long before the days of Newton. Kepler devised his laws after careful study (over some 20 years) of a large amount of meticulously recorded observations of planetary motion done by Tycho Brahe (1546–1601).
Kepler’s Laws
- The orbit of each planet about the Sun is an ellipse with the Sun at one focus.
- Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal times.
- The ratio of the squares of the periods of any two planets about the Sun is equal to the ratio of the cubes of their average distances from the Sun.
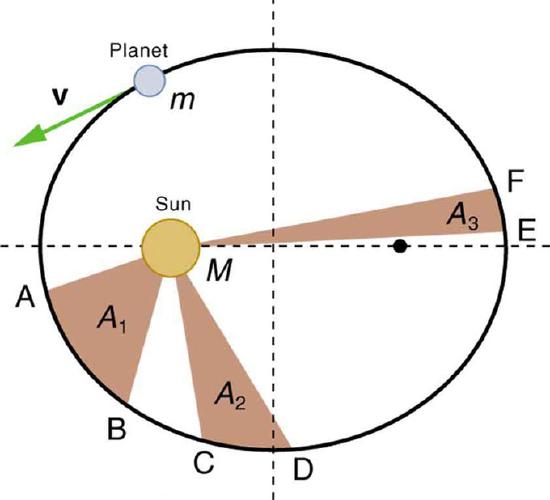
Kepler’s Second Law: The shaded regions have equal areas. It takes equal times for mm to go from A to B, from C to D, and from E to F. The mass mm moves fastest when it is closest to M. Kepler’s second law was originally devised for planets orbiting the Sun, but it has broader validity.
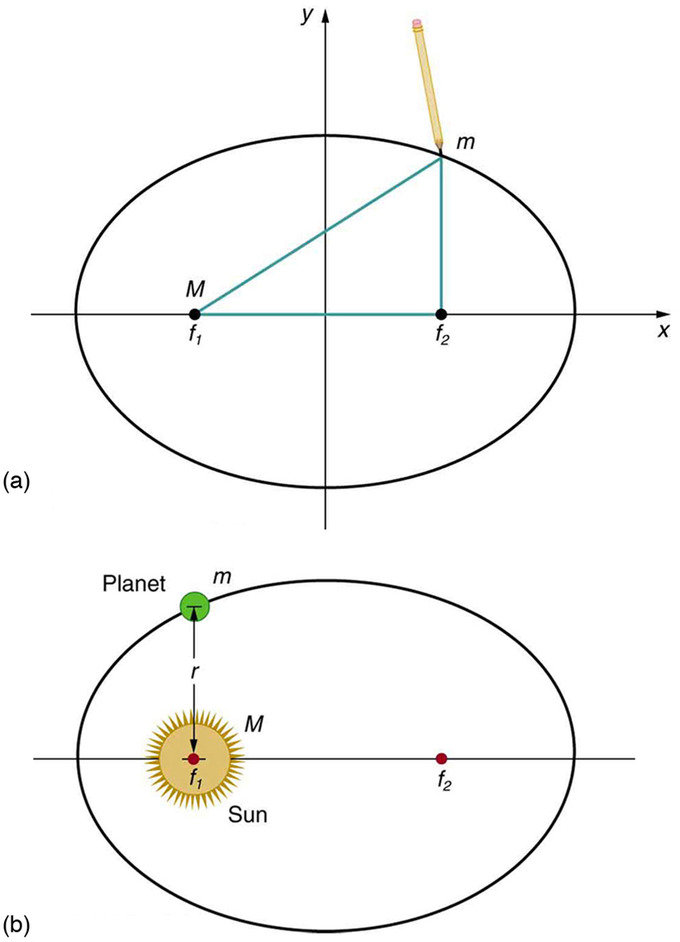
Ellipses and Kepler’s First Law: (a) An ellipse is a closed curve such that the sum of the distances from a point on the curve to the two foci (f1 and f2) is a constant. You can draw an ellipse as shown by putting a pin at each focus, and then placing a string around a pencil and the pins and tracing a line on paper. A circle is a special case of an ellipse in which the two foci coincide (thus any point on the circle is the same distance from the center). (b) For any closed gravitational orbit, m follows an elliptical path with M at one focus. Kepler’s first law states this fact for planets orbiting the Sun.
Derivation of Kepler’s Third Law For Circular Orbits
Kepler’s 3rd law is equivalent to:
T21T22=r13r23
T is the period (time for one orbit) and r is the average radius. We shall derive Kepler’s third law, starting with Newton’s laws of motion and his universal law of gravitation. We will assume a circular path (not an elliptical one) for simplicity.
Let us consider a circular orbit of a small mass mm around a large mass M, satisfying the two conditions stated at the beginning of this section. Gravity supplies the centripetal force to mass m. Therefore, for a uniform circular motion:
GmMr2=mac=mv2r
The mass m cancels, yielding:
GmMr2=v2
Now, to get at Kepler’s third law, we must get the period T into the equation. By definition, period T is the time for one complete orbit. Now the average speed v is the circumference divided by the period:
v=2πrT
Substituting this into the previous equation gives:
GMr=4π2r2T2
Solving for T2 yields:
T2=4π2GMr3
Since T2 is proportional to r3, their ratio is constant. This is Kepler’s 3rd law.
Banked and Unbacked Highway Curves
In an “ideally banked curve,” the angle θ is chosen such that one can negotiate the curve at a certain speed without the aid of friction.
learning objectives
- Derive θ for an ideally banked curve for speed
Overview
As an example of a uniform circular motion and its application, let us now consider banked curves, where the slope of the road helps you negotiate the curve. The greater the angle θ, the faster you can take the curve. Race tracks for bikes as well as cars, for example, often have steeply banked curves. In an “ideally banked curve,” the angle θ is such that you can negotiate the curve at a certain speed without the aid of friction between the tires and the road. We will derive an expression for θ for an ideally banked curve for speed vand consider an example related to it.
Uniform Circular Motion and Determining Ideal Banking Conditions
For ideal banking, the net external force equals the horizontal centripetal force in the absence of friction. The components of the normal force N in the horizontal and vertical directions must equal the centripetal force and the weight of the car, respectively. In cases in which forces are not parallel, it is most convenient to consider components along perpendicular axes—in this case, the vertical and horizontal directions.

Car on a Banked Curve: The car on this banked curve is moving away and turning to the left.
Above is a free body diagram for a car on a frictionless banked curve. The only two external forces acting on the car are its weight ww and the normal force of the road N. (A frictionless surface can only exert a force perpendicular to the surface—that is, a normal force. ) These two forces must add to give a net external force that is horizontal toward the center of curvature and has magnitude mv2r. Only the normal force has a horizontal component, and so this must equal the centripetal force—that is:
Nsinθ=mv2r
Because the car does not leave the surface of the road, the net vertical force must be zero, meaning that the vertical components of the two external forces must be equal in magnitude and opposite in direction. From the figure, we see that the vertical component of the normal force is Ncosθ, and the only other vertical force is the car’s weight. These must be equal in magnitude, thus:
Ncosθ=mg
Dividing the above equations yields:
tanθ=v2rg
Taking the inverse tangent gives:
θ=tan−1(v2rg)
for an ideally banked curve with no friction.
This expression can be understood by considering how θ depends on v and r. A large θ will be obtained for a large vand a small r. That is, roads must be steeply banked for high speeds and sharp curves. Friction helps, because it allows you to take the curve at greater or lower speed than if the curve is frictionless. Note that θ does not depend on the mass of the vehicle.
Key Points
- Under uniform circular motion, angular and linear quantities have simple relations. The length of an arc is proportional to the rotation angle and the radius. Also, v=rω.
- The acceleration responsible for the uniform circular motion is called centripetal acceleration. It is given as ac=rω2=v2r.
- Any net force causing uniform circular motion is called a centripetal force. The direction of a centripetal force is toward the center of curvature and its magnitude is mv2r=mrω2.
- The gravitational force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
- Kepler discovered laws describing planetary motion long before the days of Newton, purely based on the observations of Tycho Brahe.
- Kepler’s laws can be derived from the Newton’s universal law of gravitation and his equation of motion.
- For ideal banking, the net external force equals the horizontal centripetal force in the absence of friction.
- For ideal banking, the components of the normal force NN in the horizontal and vertical directions must equal the centripetal force and the weight of the car, respectively.
- The ideal banking condition is given as θ=tan−1(v2rg).
Key Terms
- centripetal: Directed or moving towards a center.
- asteroid: A naturally occurring solid object, which is smaller than a planet and is not a comet, that orbits a star.
- planet: A large body which directly orbits any star (or star cluster) but which has not attained nuclear fusion.
- normal force: Any force acting normal, to a surface, or perpendicular to the tangent plane.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42084/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42086/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- centripetal. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/centripetal. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42143/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42144/latest/?collection=col11406/1.7. License: CC BY: Attribution
- planet. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/planet. License: CC BY-SA: Attribution-ShareAlike
- asteroid. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/asteroid. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. January 28, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42144/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. January 28, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42144/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42086/latest/?collection=col11406/1.7. License: CC BY: Attribution
- centripetal. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/centripetal. License: CC BY-SA: Attribution-ShareAlike
- normal force. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/normal_force. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42083/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. January 28, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42144/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. January 28, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42144/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. February 6, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42086/latest/?collection=col11406/1.7. License: CC BY: Attribution

