7.2: Consequences of Special Relativity
- Last updated
- Jan 15, 2019
- Save as PDF
- Page ID
- 17124
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Formulate conclusions of the theory of special relativity, noting the assumptions that were made in deriving it
The relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer’s frame of reference.
According to the theory of special relativity, it is impossible to say in an absolute sense whether two distinct events occur at the same time if those events are separated in space, such as a car crash in London and another in New York. The question of whether the events are simultaneous is relative: in some reference frames the two accidents may happen at the same time, in other frames (in a different state of motion relative to the events) the crash in London may occur first, and still in other frames, the New York crash may occur first. If the two events are causally connected (“event A causes event B”), then the relativity of simultaneity preserves the causal order (i.e. “event A causes event B” in all frames of reference).
If we imagine one reference frame assigns precisely the same time to two events that are at different points in space, a reference frame that is moving relative to the first will generally assign different times to the two events. This is illustrated in the ladder paradox, a thought experiment which uses the example of a ladder moving at high speed through a garage.
A mathematical form of the relativity of simultaneity (“local time”) was introduced by Hendrik Lorentz in 1892, and physically interpreted (to first order in v/c) as the result of a synchronization using light signals by Henri Poincaré in 1900. However, both Lorentz and Poincaré based their conceptions on the aether as a preferred but undetectable frame of reference, and continued to distinguish between “true time” (in the aether) and “apparent” times for moving observers.
In 1905, Albert Einstein abandoned the (classical) aether and emphasized the significance of relativity of simultaneity to our understanding of space and time. He deduced the failure of absolute simultaneity from two stated assumptions: 1) the principle of relativity–the equivalence of inertial frames, such that the laws of physics apply equally in all inertial coordinate systems; 2) the constancy of the speed of light detected in empty space, independent of the relative motion of its source.
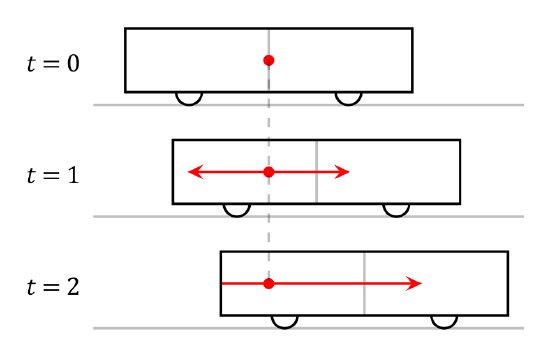
Observer Standing on the Platform: Reference frame of an observer standing on the platform (length contraction not depicted).
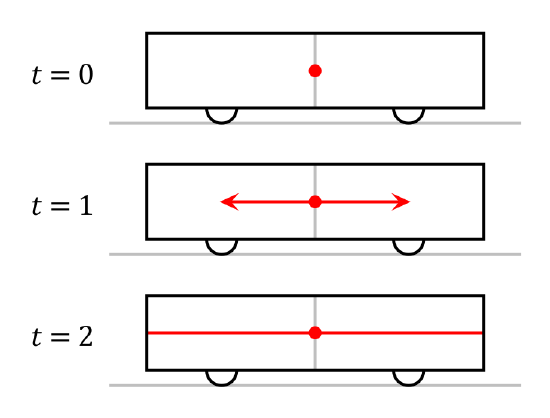
Observer Onboard the Train: The train-and-platform experiment from the reference frame of an observer onboard the train.
Time Dilation
Time dilation is an actual difference of elapsed time between two events as measured by observers moving relative to each other.
learning objectives
- Explain why time dilation can be ignored in daily life
Time dilation is an actual difference of elapsed time between two events as measured by observers either moving relative to each other.
For instance, two rocket ships (A and B) speeding past one another in space would experience time dilation. If they somehow had a clear view into each other’s ships, each crew would see the others’ clocks and movement as going too slowly. That is, inside the frame of reference of Ship A, everything is moving normally, but everything over on Ship B appears to be moving slower (and vice versa).
From a local perspective, time registered by clocks that are at rest with respect to the local frame of reference (and far from any gravitational mass) always appears to pass at the same rate. In other words, if a new ship, Ship C, travels alongside Ship A, it is “at rest” relative to Ship A. From the point of view of Ship A, new Ship C’s time would appear normal too.
The formula for determining time dilation is: Δt′=γΔt=Δt√1−v2/c2
where Δt is the time interval between two co-local events (i.e. happening at the same place) for an observer in some inertial frame (e.g. ticks on his clock), this is known as the proper time, Δt’ is the time interval between those same events, as measured by another observer, inertially moving with velocity v with respect to the former observer, v is the relative velocity between the observer and the moving clock, c is the speed of light, and γ=1√1−v2/c2
is the Lorentz factor. Thus the duration of the clock cycle of a moving clock is found to be increased: it is measured to be “running slow”. Note that for speeds below 1/10 the speed of light, Lorentz factor is approximately 1. Thus, time dilation effects and extremely small and can be safely ignored in a daily life. They become important only when an object approaches speeds on the order of 30,000 km/s (1/10 the speed of light).
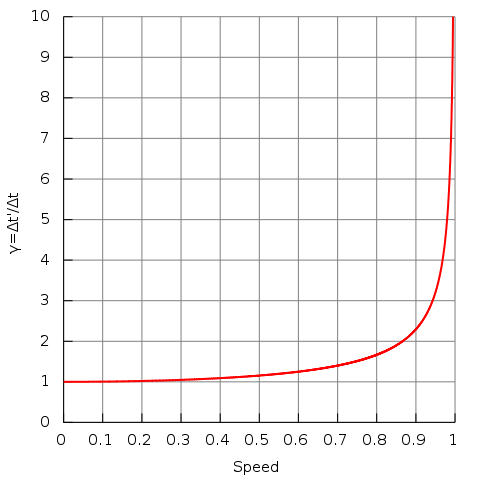
Lorentz Factor: Lorentz factor as a function of speed (in natural units where c = 1). Notice that for small speeds (less than 0.1), γ is approximately 1.
Effects of Time Dilation: The Twin Paradox and the Decay of the Muon
The twin paradox is a thought experiment: one twin makes a journey into space and returns home to find that twin remained aged more.
learning objectives
- Explain the twin paradox within the standard framework of special relativity
The twin paradox is a thought experiment in special relativity involving identical twins, one of whom makes a journey into space in a high-speed rocket and returns home to find that the twin who remained on Earth has aged more.
This occurs because special relativity shows that the faster one travels, the slower time moves for them.
This result appears puzzling because each twin sees the other twin as traveling, and so, according to a naive application of time dilation, each should paradoxically find the other to have aged more slowly. In other words, from the perspective of the rocketship, the earth is traveling away from the ship and from the perspective of the earth, the rocket is traveling away.
However, this scenario can be resolved within the standard framework of special relativity (because the twins are not equivalent; the space twin experienced additional, asymmetrical acceleration when switching direction to return home), and therefore is not a paradox in the sense of a logical contradiction.
The Earth and the ship are not in a symmetrical relationship: regardless of whether we view the situation from the perspective of the Earth or the ship, the ship experiences additional acceleration forces. The ship has a turnaround in which it accelerates and changes direction whereas the earth does not. Since there is no symmetry, it is not paradoxical if one twin is younger than the other. Nevertheless twin paradox is useful as a demonstration that special relativity is self-consistent.
In the spacetime diagram, drawn for the reference frame of the Earth-based twin, that twin’s world line coincides with the vertical axis (his position is constant in space, moving only in time). On the first leg of the trip, the second twin moves to the right (black sloped line); and on the second leg, back to the left. Blue lines show the planes of simultaneity for the traveling twin during the first leg of the journey; red lines, during the second leg. Just before turnaround, the traveling twin calculates the age of the Earth-based twin by measuring the interval along the vertical axis from the origin to the upper blue line. Just after turnaround, if he recalculates, he’ll measure the interval from the origin to the lower red line. In a sense, during the U-turn the plane of simultaneity jumps from blue to red and very quickly sweeps over a large segment of the world line of the Earth-based twin. The traveling twin reckons that there has been a jump discontinuity in the age of the Earth-based twin.
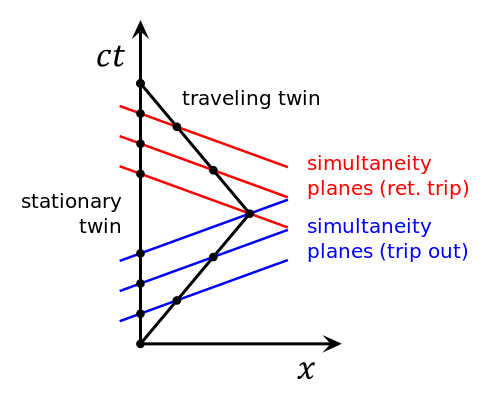
Spacetime Diagram of the Twin Paradox: Spacetime diagram of the twin paradox. Time is relative, but both twins are not equivalent (the ship experiences additional acceleration to changes the direction of travel).
Length Contraction
Objects that are moving undergo a length contraction along the dimension of motion; this effect is only significant at relativistic speeds.
learning objectives
- Explain why length contraction can be ignored in daily life
Length contraction is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer. Length contraction arises due to the fact that the speed of light in a vacuum is constant in any frame of reference. By taking this into account, as well as some geometrical considerations, we will show how perceived time and length are affected.
Example 7.2.1:
Let us imagine a simple clock system that consists of two mirrors A and B in a vacuum. A light pulse bounces between the two mirrors. The separation of the mirrors is L, and the clock ticks once each time the light pulse hits a given mirror. Now imagine that the clock is at rest. The time that it will take for the light pulse to go from mirror A to mirror B and then back to mirror A be can be described by:
Δt=2Lc
where c is the speed of light. Now imagine that the clock is moving in the horizontal direction relative to a stationary observer. The light pulse is emitted from mirror A. To the stationary observer, it appears that the light pulse has a longer path to travel because by the time the light reaches mirror B the clock has already moved somewhat in the horizontal direction. This is the same case for the light pulse on its way back. The stationary observer will perceive that it will take the light a total of:
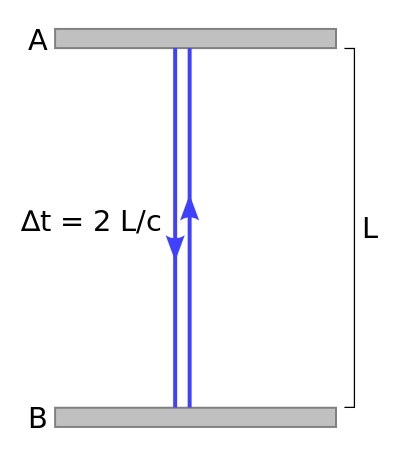
Geometry for a Clock at Rest: This illustrates the path that light must traverse when the clock is at rest.
Δt′=2Dc
to traverse its path. We can see that D is longer than L, so that means that.
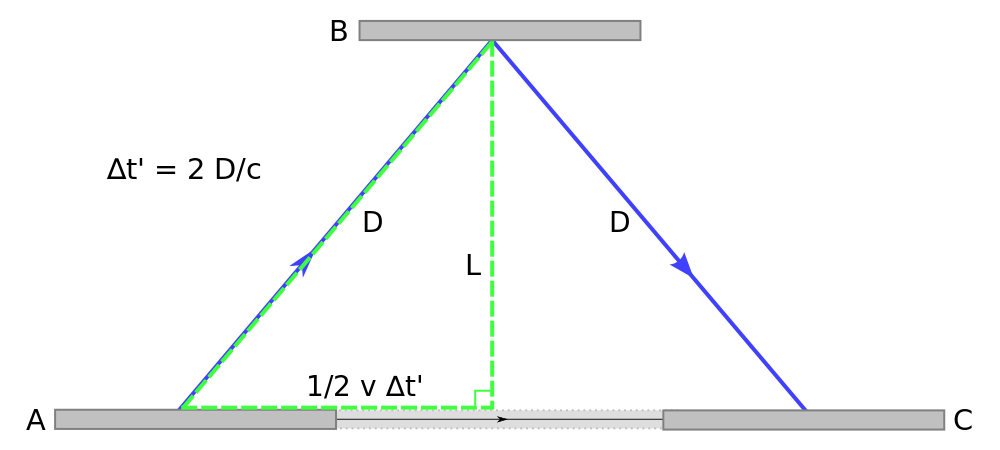
Geometry for a Moving Clock: This illustrates the path that light must traverse when the clock is moving from the perspective of a stationary observer.
Example 7.2.2:
We have established that in a frame of reference that is moving relative to the clock (the stationary observer is moving in the clock’s frame of reference), the clock appears to run more slowly. Now let us imagine that we want to measure the length of a ruler. This time let us imagine that you are moving with velocity v. You can mathematically determine the length of the ruler in your frame of reference (L‘) by multiplying your velocity (v) by the time that you perceive that it takes you to pass by the ruler (t‘). Expressing this in equation form, L‘ = vt‘. Now, if someone in the ruler’s rest frame wanted to determine the length of the ruler, they could do the following. They could mathematically determine the length of the ruler in their frame of reference (L) by multiplying your velocity (v) by the time that they perceive that it takes you to pass by the ruler (t). This is expressed in the following equation: L = vt. Just as in the clock explanation, the ruler appears to be moving in your frame of reference, so t will be longer than t‘ (your time interval). Consequently, the length of the ruler will appear to be shorter in your frame of reference (the phenomenon of length contraction occurred).
The effect of length contraction is negligible at everyday speeds and can be ignored for all regular purposes. Length contraction becomes noticeable at a substantial fraction of the speed of light (as illustrated in ) with the contraction only in the direction parallel to the direction in which the observed body is travelling.
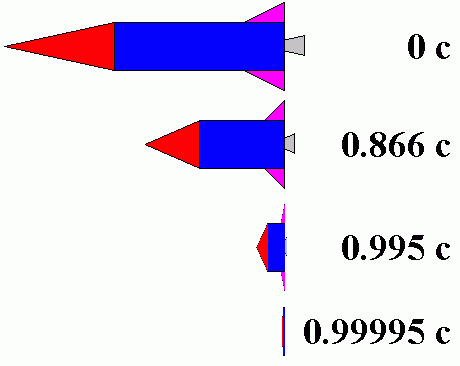
Observed Length of an Object: Observed length of an object at rest and at different speeds
Example 7.2.3:
For example, at a speed of 13,400,000 m/s (30 million mph,.0447c), the length is 99.9 percent of the length at rest; at a speed of 42,300,000 m/s (95 million mph, 0.141c), the length is still 99 percent. As the magnitude of the velocity approaches the speed of light, the effect becomes dominant.The mathematical formula for length contraction is:
L=L0γ(v)=L0√1−v2c2
where L0 is the proper length (the length of the object in its rest frame); L is the length observed by an observer in relative motion with respect to the object; v is the relative velocity between the observer and the moving object; c is the speed of light; and the Lorentz factor is defined as:
γ(v)=1√1−v2/c2
In this equation it is assumed that the object is parallel with its line of movement. For the observer in relative movement, the length of the object is measured by subtracting the simultaneously measured distances of both ends of the object. An observer at rest viewing an object traveling very close to the speed of light would observe the length of the object in the direction of motion as very close to zero.
Key Points
- According to the theory of special relativity, it is impossible to say in an absolute sense whether two distinct events occur at the same time if those events are separated in space.
- A mathematical form of the relativity of simultaneity was introduced by Hendrik Lorentz and physically interpreted by Henri Poincaré. The conceptions were based on the aether as a preferred but undetectable frame of reference.
- Albert Einstein deduced the failure of absolute simultaneity from two assumptions: 1) the principle of relativity; 2) the constancy of the speed of light detected in empty space, independent of the relative motion of its source.
- Time dilation effects are extremely small for speeds below 1/10 the speed of light and can be safely ignored at daily life.
- Time dilation effects become important when an object approaches speeds on the order of 30,000 km/s (1/10 the speed of light).
- The formula for determining time dilation is: Δt′=Δt√1−v2/c2.
- From a naive application of time dilation, each twin should paradoxically find the other to have aged more slowly.
- The scenario is resolved within the standard framework of special relativity: the twins are not equivalent, the space twin experiences additional, asymmetrical acceleration when switching direction to return home.
- Twin paradox is useful as a demonstration that special relativity is self-consistent.
- Length contraction is negligible at everyday speeds and can be ignored for all regular purposes.
- Length contraction becomes noticeable at a substantial fraction of the speed of light with the contraction only in the direction parallel to the direction in which the observed body is travelling.
- An observer at rest viewing an object travelling very close to the speed of light would observe the length of the object in the direction of motion as very near zero.
Key Terms
- aether: A space-filling substance or field, thought to be necessary as a transmission medium for the propagation of electromagnetic or gravitational forces.
- special relativity: A theory that (neglecting the effects of gravity) reconciles the principle of relativity with the observation that the speed of light is constant in all frames of reference.
- speed of light: the speed of electromagnetic radiation in a perfect vacuum: exactly 299,792,458 meters per second by definition
- time dilation: The slowing of the passage of time experienced by objects in motion relative to an observer; measurable only at relativistic speeds.
- Lorentz factor: The factor, used in special relativity, to calculate the degree of time dilation, length contraction and relativistic mass of an object moving relative to an observer.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- special relativity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/special_relativity. License: CC BY-SA: Attribution-ShareAlike
- Relativity of simultaneity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Relativity_of_simultaneity. License: CC BY-SA: Attribution-ShareAlike
- Simultaneity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Simultaneity. License: CC BY-SA: Attribution-ShareAlike
- aether. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/aether. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/commons/thumb/7/72/Traincar_Relativity2.svg/800px-Traincar_Relativity2.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/commons/thumb/c/ce/Traincar_Relativity1.svg/735px-Traincar_Relativity1.svg.png. License: CC BY-SA: Attribution-ShareAlike
- time dilation. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/time_dilation. License: CC BY-SA: Attribution-ShareAlike
- speed of light. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/speed_of_light. License: CC BY-SA: Attribution-ShareAlike
- Lorentz factor. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/Lorentz_factor. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/7/72/Traincar_Relativity2.svg/800px-Traincar_Relativity2.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/c/ce/Traincar_Relativity1.svg/735px-Traincar_Relativity1.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/commons/thumb/4/4f/Time_dilation.svg/480px-Time_dilation.svg.png. License: CC BY-SA: Attribution-ShareAlike
- special relativity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/special_relativity. License: CC BY-SA: Attribution-ShareAlike
- Twin paradox. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Twin_paradox. License: CC BY-SA: Attribution-ShareAlike
- time dilation. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/time_dilation. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/7/72/Traincar_Relativity2.svg/800px-Traincar_Relativity2.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/c/ce/Traincar_Relativity1.svg/735px-Traincar_Relativity1.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/4/4f/Time_dilation.svg/480px-Time_dilation.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/commons/thumb/c/ce/Twin_Paradox_Minkowski_Diagram.svg/485px-Twin_Paradox_Minkowski_Diagram.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Length contraction. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Length_contraction. License: CC BY-SA: Attribution-ShareAlike
- Time dilation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Time_dilation%23Simple_inference_of_time_dilation_due_to_relative_velocity. License: CC BY-SA: Attribution-ShareAlike
- speed of light. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/speed_of_light. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/7/72/Traincar_Relativity2.svg/800px-Traincar_Relativity2.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/c/ce/Traincar_Relativity1.svg/735px-Traincar_Relativity1.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/4/4f/Time_dilation.svg/480px-Time_dilation.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/commons/thumb/c/ce/Twin_Paradox_Minkowski_Diagram.svg/485px-Twin_Paradox_Minkowski_Diagram.svg.png. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Creation Wiki. Located at: http://creationwiki.org/images/9/91/Srlc1.png. License: Public Domain: No Known Copyright
- Time dilation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Time_dilation%23Simple_inference_of_time_dilation_due_to_relative_velocity. License: CC BY: Attribution
- Time dilation. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Time_dilation%23Simple_inference_of_time_dilation_due_to_relative_velocity. License: CC BY: Attribution

