10.3: Archimedes’ Principle
- Last updated
- Jan 14, 2019
- Save as PDF
- Page ID
- 16994

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Calculate the direction of the buoyancy force
When you rise from soaking in a warm bath, your arms may feel strangely heavy. This effect is due to the loss of the buoyant support of the water. What creates this buoyant force ? Why is it that some things float and others do not? Do objects that sink get any support at all from the fluid? Is your body buoyed by the atmosphere, or are only helium balloons affected?
Buoyant Force: Cause and Calculation
We find the answers to the above questions in the fact that in any given fluid, pressure increases with depth. When an object is immersed in a fluid, the upward force on the bottom of an object is greater than the downward force on the top of the object. The result is a net upward force (a buoyant force) on any object in any fluid. If the buoyant force is greater than the object’s weight, the object will rise to the surface and float. If the buoyant force is less than the object’s weight, the object will sink. If the buoyant force equals the object’s weight, the object will remain suspended at that depth. The buoyant force is always present in a fluid, whether an object floats, sinks or remains suspended.
The buoyant force is a result of pressure exerted by the fluid. The fluid pushes on all sides of an immersed object, but as pressure increases with depth, the push is stronger on the bottom surface of the object than in the top (as seen in ).
You can calculate the buoyant force on an object by adding up the forces exerted on all of an object’s sides. For example, consider the object shown in.
The top surface has area A and is at depth h1; the pressure at that depth is:
P1=h1ρg,
where ρρ is the density of the fluid and g≈9.81ms2 is the gravitational acceleration. The magnitude of the force on the top surface is:
F1=P1A=h1ρgA.
This force points downwards. Similarly, the force on the bottom surface is:
F2=P2A=h2ρgA
and points upwards. Because it is cylindrical, the net force on the object’s sides is zero—the forces on different parts of the surface oppose each other and cancel exactly. Thus, the net upward force on the cylinder due to the fluid is:
FB=F2−F1=ρgA(h2−h1)
The Archimedes Principle
Although calculating the buoyant force in this way is always possible it is often very difficult. A simpler method follows from the Archimedes principle, which states that the buoyant force exerted on a body immersed in a fluid is equal to the weight of the fluid the body displaces. In other words, to calculate the buoyant force on an object we assume that the submersed part of the object is made of water and then calculate the weight of that water (as seen in ).
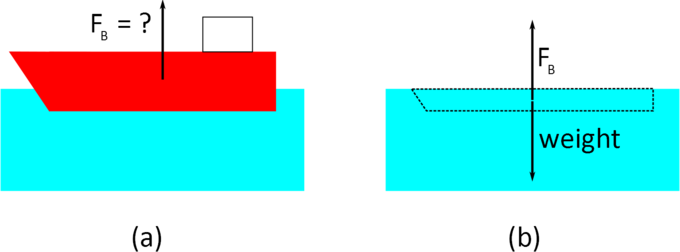
Archimedes principle: The buoyant force on the ship (a) is equal to the weight of the water displaced by the ship—shown as the dashed region in (b).
The principle can be stated as a formula:
FB=wfl
The reasoning behind the Archimedes principle is that the buoyancy force on an object depends on the pressure exerted by the fluid on its submerged surface. Imagine that we replace the submerged part of the object with the fluid in which it is contained, as in (b). The buoyancy force on this amount of fluid must be the same as on the original object (the ship). However, we also know that the buoyancy force on the fluid must be equal to its weight, as the fluid does not sink in itself. Therefore, the buoyancy force on the original object is equal to the weight of the “displaced fluid” (in this case, the water inside the dashed region (b)).
The Archimedes principle is valid for any fluid—not only liquids (such as water) but also gases (such as air). We will explore this further as we discuss applications of the principle in subsequent sections.
Archimedes’ Principle – Simple Example: We use Archimedes’ Principle to determine the number of penguins an ice float can dryly support.
Complete Submersion
The buoyancy force on a completely submerged object of volume is FB=Vρg.
learning objectivies
- Identify factors determining the buoyancy force on a completely submerged object
The Archimedes principle is easiest to understand and apply in the case of entirely submersed objects. In this section we discuss a few relevant examples. In general, the buoyancy force on a completely submerged object is given by the formula:
FB=Vρg,
where V is the volume of the object, ρ is the density of the fluid, and g is gravitational acceleration. This follows immediately from the Archimedes’ principle, and the fact that the object is completely submerged (and so the volume of the fluid displaced is just the volume of the object).
Cylinder
In the previous section, we calculated the buoyancy force on a cylinder (shown in ) by considering the force exerted on each of the cylinder’s sides. Now, we’ll calculate this force using Archimedes’ principle. The buoyancy force on the cylinder is equal to the weight of the displaced fluid. This weight is equal to the mass of the displaced fluid multiplied by the gravitational acceleration:
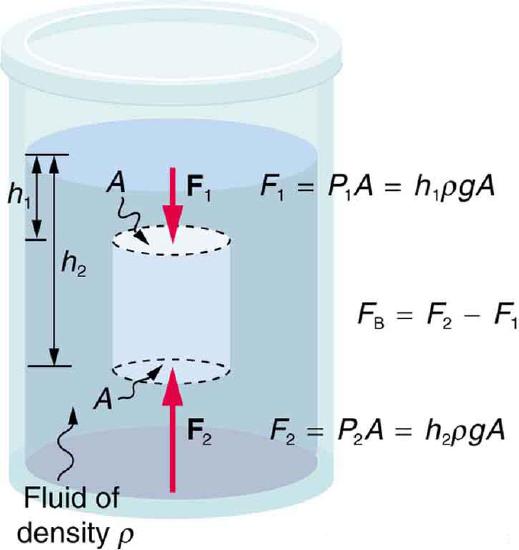
Buoyant force: The fluid pushes on all sides of a submerged object. However, because pressure increases with depth, the upward push on the bottom surface (F2) is greater than the downward push on the top surface (F1). Therefore, the net buoyant force is always upwards.
FB=wfl=mflg
The mass of the displaced fluid is equal to its volume multiplied by its density:
mfl=Vflρ
However (and this is the crucial point), the cylinder is entirely submerged, so the volume of the displaced fluid is just the volume of the cylinder (see ), and:
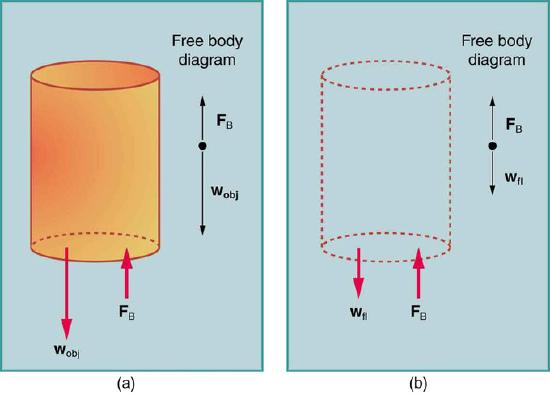
Archimedes principle: The volume of the fluid displaced (b) is the same as the volume of the original cylinder (a).
mfl=Vflρ=Vcylinderρ.
The volume of a cylinder is the area of its base multiplied by its height, or in our case:
Vcylinder=A(h2−h1).
Therefore, the buoyancy force on the cylinder is:
FB=mflg=Vcylinderρg=(h1−h2)ρgA.
This is the same result obtained in the previous section by considering the force due to the pressure exerted by the fluid.
Helium Airship
Consider the USS Macon, a helium-filled airship (shown in ). Its envelope (the “balloon”) contained 184,059.5 cubic meters of helium. Ignoring the small volume of the gondola, what was the buoyancy force on this airship? If the airship weighed 108,000 kg, how much cargo could it carry? Assume the density of air is 1.225 kg per meter cubed. The buoyancy force on an airship is due to the air in which it is immersed. Although we don’t know the exact shape of the airship, we know its volume and the density of the air, and thus we can calculate the buoyancy force:

Helium airship: The USS Macon, a 1930s helium-filled airship.
FB=Vρg=184,059.5kg×1.225kgm3×9.81ms2≈2.212×106N
To find the cargo capacity of the airship, we subtract the weight of the airship from the buoyancy force:
Fcargo=FB−mg=2.21×106N−1.08×105kg×9.81ms2=1.15×106N
The mass the airship can carry is:
mcargo=Fcargog=1.2×105kg=120tons.
Flotation
An object floats if the buoyancy force exerted on it by the fluid balances its weight.
learning objectives
- Express the relationship between the buoyancy force and the weight for a floating object
Why do some objects float, but others don’t? If you put a metal coin into a glass of water it will sink. But most ships are built of metal, and they float. So how is this possible?
Condition for Flotation
An object will float if the buoyancy force exerted on it by the fluid balances its weight, i.e. if FB=mgFB=mg.
But the Archimedes principle states that the buoyant force is the weight of the fluid displaced. So, for a floating object on a liquid, the weight of the displaced liquid is the weight of the object. Thus, only in the special case of floating does the buoyant force acting on an object equal the object’s weight. Consider a one-ton block of solid iron. As iron is nearly eight times denser than water, it displaces only 1/8 ton of water when submerged, which is not enough to keep it afloat. Suppose the same iron block is reshaped into a bowl. It still weighs one ton, but when it is put in water, it displaces a greater volume of water than when it was a block. The deeper the iron bowl is immersed, the more water it displaces, and the greater the buoyant force acting on it. When the buoyant force equals one ton, it will sink no further.
When any boat displaces a weight of water equal to its own weight, it floats. This is often called the “principle of flotation” where a floating object displaces a weight of fluid equal to its own weight. Every ship, submarine, and dirigible must be designed to displace a weight of fluid equal to its own weight. A 10,000-ton ship must be built wide enough to displace 10,000 tons of water before it sinks too deep in the water. The same is true for vessels in air (as air is a fluid): A dirigible that weighs 100 tons displaces at least 100 tons of air; if it displaces more, it rises; if it displaces less, it falls. If the dirigible displaces exactly its weight, it hovers at a constant altitude.
Flotation and Density
Density plays a crucial role in Archimedes’ principle. The average density of an object is what ultimately determines whether it floats. If its average density is less than that of the surrounding fluid, it will float. This is because the fluid, having a higher density, contains more mass and thus more weight in the same volume. The buoyant force, which equals the weight of the fluid displaced, is thus greater than the weight of the object. Likewise, an object denser than the fluid will sink. The extent to which a floating object is submerged depends on how the object’s density is related to that of the fluid. For example, an unloaded ship has a lower density, and less of it is submerged compared with the same ship loaded with cargo. We can derive a quantitative expression for the fraction submerged by considering density. The fraction submerged is the ratio of the volume submerged to the volume of the object, or

Density and Submersion: An unloaded ship (a) floats higher in the water than a loaded ship (b).
fractionsubmerged=VsubVobj=VflVobj
The volume submerged equals the volume of fluid displaced, which we call Vfl. Now we can obtain the relationship between the densities by substituting ρ=mV into the expression. This gives
fractionsubmerged=mfl/ρflmobj/ˉρobj
where ˉρobj is the average density of the object and ρflρflis the density of the fluid. Since the object floats, its mass and that of the displaced fluid are equal, and so they cancel from the equation, leaving
fractionsubmerged=ˉρobjρfl.
There are a couple things to note about this expression:
- Note that it mentions the average density of the object. This can be much less than the density of the material the object is made of. For instance, a steel ship is actually mostly filled with air (think of the corridors, cargo holds, etc.), so its average density is between that of air and steel. To be more precise, the average density is defined as the total mass of an object divided by its total volume: ˉρ=mV.
- This formula makes sense only if the density of the object is smaller than the density of the fluid. Otherwise, the fraction submerged becomes greater than one—a sign that the object does not float at all, but it sinks!
Key Points
- The buoyancy force is caused by the pressure exerted by the fluid in which an object is immersed.
- The buoyancy force always points upwards because the pressure of a fluid increases with depth.
- You can calculate the buoyancy force either directly by computing the force exerted on each of the object’s surfaces, or indirectly by finding the weight of the displaced fluid.
- If an object is completely submerged, the volume of the fluid displaced is equal to the volume of the object.
- The buoyancy force on hot-air balloons, dirigibles and other objects can be calculated by assuming that they are entirely submerged in air.
- The buoyancy force does not depend on the shape of the object, only on its volume.
- The buoyancy force experienced by an object depends on its shape.
- The fraction of an object’s volume that’s submerged is given by the ratio of its average density to that of the fluid: ˉρobjρfl.
- An object floats if the buoyancy force exerted on it by the fluid balances its weight.
Key Terms
- buoyant force: An upward force exerted by a fluid that opposes the weight of an immersed object.
- Archimedes principle: The buoyant force exerted on a body immersed in a fluid is equal to the weight of the fluid the body displaces.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42196/latest/?collection=col11406/latest. License: CC BY: Attribution
- Archimedes principle. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Archimedes%20principle. License: CC BY-SA: Attribution-ShareAlike
- buoyant force. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/buoyant%20force. License: CC BY-SA: Attribution-ShareAlike
- Archimedes' Principle - Simple Example. Located at: http://www.youtube.com/watch?v=Ls4aig_pg3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/50953ccfe4b0b4558d8e546b/Ships.png. License: Public Domain: No Known Copyright
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42196/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Archimedes principle. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Archimedes%20principle. License: CC BY-SA: Attribution-ShareAlike
- Archimedes' Principle - Simple Example. Located at: http://www.youtube.com/watch?v=Ls4aig_pg3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/50953ccfe4b0b4558d8e546b/Ships.png. License: Public Domain: No Known Copyright
- USS Macon F9C. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/File:USS_Macon_F9C.jpg. License: Public Domain: No Known Copyright
- OpenStax College, College Physics. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42196/latest/?collection=col11406/latest. License: CC BY: Attribution
- OpenStax College, College Physics. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42196/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Archimedes principle. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Archimedes_principle. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42196/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Archimedes principle. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Archimedes%20principle. License: CC BY-SA: Attribution-ShareAlike
- Archimedes' Principle - Simple Example. Located at: http://www.youtube.com/watch?v=Ls4aig_pg3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/50953ccfe4b0b4558d8e546b/Ships.png. License: Public Domain: No Known Copyright
- USS Macon F9C. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/File:USS_Macon_F9C.jpg. License: Public Domain: No Known Copyright
- OpenStax College, College Physics. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42196/latest/?collection=col11406/latest. License: CC BY: Attribution
- OpenStax College, College Physics. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42196/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. November 3, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42196/latest/?collection=col11406/1.7. License: CC BY: Attribution


