3.4: Vector Addition and Subtraction- Analytical Methods
- Last updated
- Jul 16, 2020
- Save as PDF
- Page ID
- 26495
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Understand the rules of vector addition and subtraction using analytical methods.
- Apply analytical methods to determine vertical and horizontal component vectors.
- Apply analytical methods to determine the magnitude and direction of a resultant vector.
Analytical methods of vector addition and subtraction employ geometry and simple trigonometry rather than the ruler and protractor of graphical methods. Part of the graphical technique is retained, because vectors are still represented by arrows for easy visualization. However, analytical methods are more concise, accurate, and precise than graphical methods, which are limited by the accuracy with which a drawing can be made. Analytical methods are limited only by the accuracy and precision with which physical quantities are known.
Resolving a Vector into Perpendicular Components
Analytical techniques and right triangles go hand-in-hand in physics because (among other things) motions along perpendicular directions are independent. We very often need to separate a vector into perpendicular components. For example, given a vector like A in Figure 3.4.1, we may wish to find which two perpendicular vectors, Ax and Ay, add to produce it.
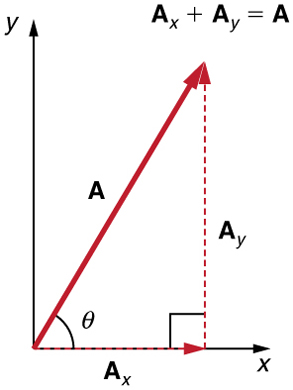
Figure 3.4.1:The vector A, with its tail at the origin of an x, y-coordinate system, is shown together with its x- and y-components, Ax and Ay. These vectors form a right triangle. The analytical relationships among these vectors are summarized below.
Ax and Ay are defined to be the components of A along the x- and y-axes. The three vectors A,Ax, and Ay form a right triangle:
Ax+Ay=A.
Note that this relationship between vector components and the resultant vector holds only for vector quantities (which include both magnitude and direction). The relationship does not apply for the magnitudes alone. For example, if Ax=3m east, Ay=4m north, and A=5mnorth-east, then it is true that the vectors Ax+Ay=A. However, it is not true that the sum of the magnitudes of the vectors is also equal. That is,
3m+4m≠5m
Thus,
Ax+Ay≠A
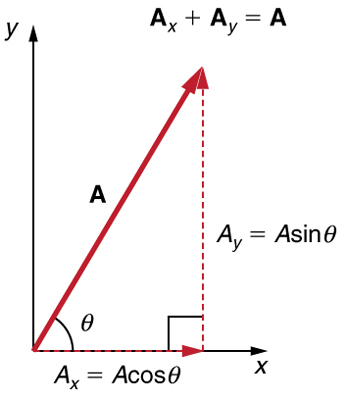
If the vector A is known, then its magnitude A (its length) and its angle \displaystyle θ (its direction) are known. To find \displaystyle A_x and \displaystyle A_y, its x- and y-components, we use the following relationships for a right triangle.
\displaystyle A_x=Acosθ
and
\displaystyle A_y=Asinθ.
Suppose, for example, that A is the vector representing the total displacement of the person walking in a city considered in Kinematics in Two Dimensions: An Introduction and Vector Addition and Subtraction: Graphical Methods.
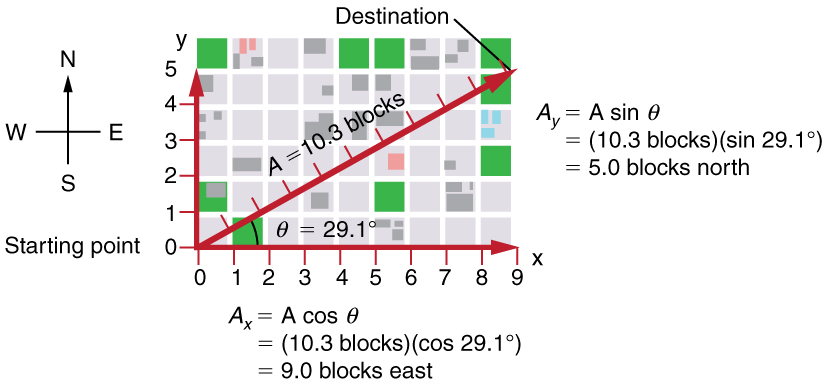
Figure \PageIndex{3}: We can use the relationships \displaystyle A_x=Acosθ and \displaystyle A_y=Asinθ to determine the magnitude of the horizontal and vertical component vectors in this example.
Then \displaystyle A=10.3 blocks and \displaystyle θ=29.1º, so that
\displaystyle A_x=A\cos θ=(10.3 blocks)(\cos 29.1º)=9.0 \quad blocks
\displaystyle A_y=A\sin θ=(10.3 blocks)(\sin 29.1º)=5.0 \quad blocks
Calculating a Resultant Vector
If the perpendicular components \displaystyle A_x and \displaystyle A_y of a vector \displaystyle A are known, then A can also be found analytically. To find the magnitude \displaystyle A and direction \displaystyle θ of a vector from its perpendicular components \displaystyle A_x and \displaystyle A_y, we use the following relationships:
\displaystyle A=\sqrt{A_{x^2}+A_{y^2}}
\displaystyle θ=tan^{−1}(A_y/A_x)
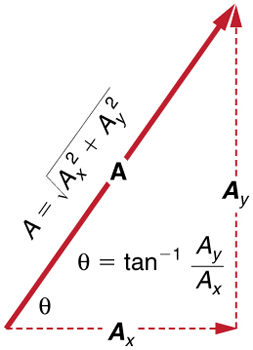
Figure \PageIndex{4}: The magnitude and direction of the resultant vector can be determined once the horizontal and vertical components \displaystyle A_x and \displaystyle A_y have been determined.
Note that the equation \displaystyle A=\sqrt{A^2_x+A^2_y} is just the Pythagorean theorem relating the legs of a right triangle to the length of the hypotenuse. For example, if \displaystyle A_x and \displaystyle A_y are 9 and 5 blocks, respectively, then \displaystyle A=\sqrt{9^2+5^2}=10.3 blocks, again consistent with the example of the person walking in a city. Finally, the direction is \displaystyle θ=tan^{–1}(5/9)=29.1º, as before.
DETERMINING VECTORS AND VECTOR COMPONENTS WITH ANALYTICAL METHODS
Equations \displaystyle A_x=Acosθ and \displaystyle A_y=Asinθ are used to find the perpendicular components of a vector—that is, to go from \displaystyle A and \displaystyle θ to \displaystyle A_x and \displaystyle A_y. Equations \displaystyle A=\sqrt{A^2_x+A^2_y} and \displaystyle θ=tan^{–1}(A_y/A_x) are used to find a vector from its perpendicular components—that is, to go from \displaystyle A_x and \displaystyle A_y to \displaystyle A and \displaystyle θ. Both processes are crucial to analytical methods of vector addition and subtraction.
Adding Vectors Using Analytical Methods
To see how to add vectors using perpendicular components, consider Figure \PageIndex{5}, in which the vectors \displaystyle A and \displaystyle B are added to produce the resultant \displaystyle R.
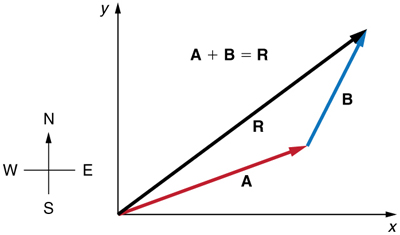
Figure \PageIndex{5}: Vectors \displaystyle A and\displaystyle B are two legs of a walk, and \displaystyle R is the resultant or total displacement. You can use analytical methods to determine the magnitude and direction of \displaystyle R.
If \displaystyle A and \displaystyle B represent two legs of a walk (two displacements), then \displaystyle R is the total displacement. The person taking the walk ends up at the tip of R. There are many ways to arrive at the same point. In particular, the person could have walked first in the x-direction and then in the y-direction. Those paths are the x- and y-components of the resultant, \displaystyle R_x and \displaystyle R_y. If we know \displaystyle R_x and \displaystyle R_y, we can find \displaystyle R and \displaystyle θ using the equations \displaystyle A=\sqrt{A_x^2+A_y^2} and \displaystyle θ=tan^{–1}(A_y/A_x). When you use the analytical method of vector addition, you can determine the components or the magnitude and direction of a vector.
Step 1. Identify the x- and y-axes that will be used in the problem. Then, find the components of each vector to be added along the chosen perpendicular axes. Use the equations \displaystyle A_x=Acosθ and \displaystyle A_y=Asinθ to find the components. In Figure, these components are \displaystyle A_x, A_y, B_x, and \displaystyle B_y. The angles that vectors \displaystyle A and \displaystyle B make with the x-axis are \displaystyle θ_A and \displaystyle θ_B, respectively.
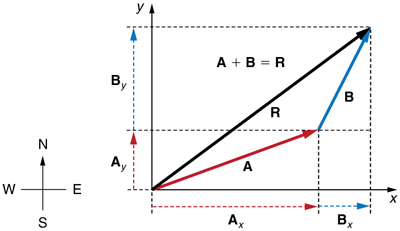
Figure \PageIndex{6}: To add vectors \displaystyle A and \displaystyle B, first determine the horizontal and vertical components of each vector. These are the dotted vectors \displaystyle A_x, A_y, B_x and \displaystyle B-y shown in the image.
Step 2. Find the components of the resultant along each axis by adding the components of the individual vectors along that axis. That is, as shown in Figure \(\PageIndex{7}\,
\displaystyle R_x=A_x+B_x
and
\displaystyle R_y=A_y+B_y.
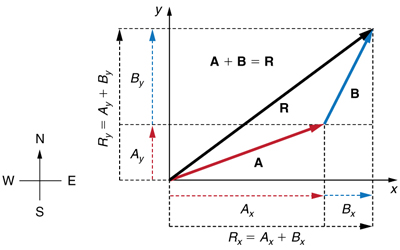
Figure \PageIndex{7}: The magnitude of the vectors \displaystyle A_x and \displaystyle B_x add to give the magnitude \displaystyle R_x of the resultant vector in the horizontal direction. Similarly, the magnitudes of the vectors \displaystyle A_y and \displaystyle B_y add to give the magnitude \displaystyle R_y of the resultant vector in the vertical direction.
Components along the same axis, say the x-axis, are vectors along the same line and, thus, can be added to one another like ordinary numbers. The same is true for components along the y-axis. (For example, a 9-block eastward walk could be taken in two legs, the first 3 blocks east and the second 6 blocks east, for a total of 9, because they are along the same direction.) So resolving vectors into components along common axes makes it easier to add them. Now that the components of R are known, its magnitude and direction can be found.
Step 3. To get the magnitude \displaystyle R of the resultant, use the Pythagorean theorem:
\displaystyle R=\sqrt{R^2_x+R^2_y}
Step 4. To get the direction of the resultant:
\displaystyle θ=tan^{−1}(R_y/R_x)
The following example illustrates this technique for adding vectors using perpendicular components.
Example \displaystyle \PageIndex{1}: Adding Vectors Using Analytical Methods
Add the vector \displaystyle A to the vector \displaystyle B shown in Figure, using perpendicular components along the x- and y-axes. The x- and y-axes are along the east–west and north–south directions, respectively. Vector \displaystyle A represents the first leg of a walk in which a person walks \displaystyle 53.0 m in a direction \displaystyle 20.0º north of east. Vector \displaystyle B represents the second leg, a displacement of \displaystyle 34.0 m in a direction \displaystyle 63.0º north of east.
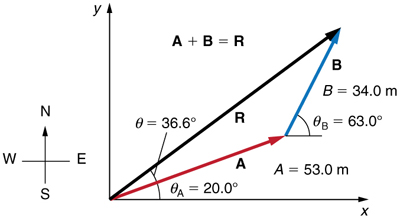
Figure \PageIndex{8}: Vector \displaystyle A has magnitude \displaystyle 53.0 m and direction \displaystyle 20.0º north of the x-axis. Vector B has magnitude \displaystyle 34.0 m and direction \displaystyle 63.0º north of the x-axis. You can use analytical methods to determine the magnitude and direction of \displaystyle R.
Strategy
The components of \displaystyle A and \displaystyle B along the x- and y-axes represent walking due east and due north to get to the same ending point. Once found, they are combined to produce the resultant.
Solution
Following the method outlined above, we first find the components of \displaystyle A and \displaystyle B along the x- and y-axes. Note that \displaystyle A=53.0 m, θ_A=20.0º, B=34.0 m, and \displaystyle θ_B=63.0º. We find the x-components by using \displaystyle A_x=Acosθ, which gives
\displaystyle A_x=Acosθ_A=(53.0 m)(cos 20.0º)(53.0 m)(0.940)=49.8 m
and
\displaystyle B_x=Bcosθ_B=(34.0 m)(cos 63.0º)(34.0 m)(0.454)=15.4 m.
Similarly, the y-components are found using \displaystyle A_y=Asinθ_A:
\displaystyle A_y=Asinθ_A=(53.0 m)(sin 20.0º)(53.0 m)(0.342)=18.1 m
and
\displaystyle B_y=Bsinθ_B=(34.0 m)(sin 63.0º)(34.0 m)(0.891)=30.3 m.
The x- and y-components of the resultant are thus
\displaystyle R_x=A_x+B_x=49.8 m+15.4 m=65.2 m
and
\displaystyle R_y=A_y+B_y=18.1 m+30.3 m=48.4 m.
Now we can find the magnitude of the resultant by using the Pythagorean theorem:
\displaystyle R=\sqrt{R^2_x+R^2_y}=\sqrt{(65.2)^2+(48.4)^2m}
so that
\displaystyle R=81.2 m.
Finally, we find the direction of the resultant:
\displaystyle θ=tan^{−1}(R_y/R_x)=+tan^{−1}(48.4/65.2).
Thus,
\displaystyle θ=tan^{−1}(0.742)=36.6º.
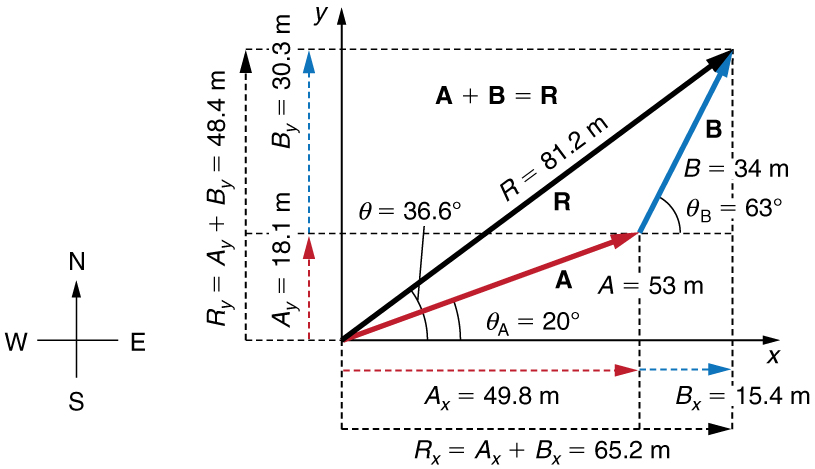
Figure \PageIndex{9}: Using analytical methods, we see that the magnitude of \displaystyle R is \displaystyle 81.2 m and its direction is \displaystyle 36.6º north of east.
Discussion
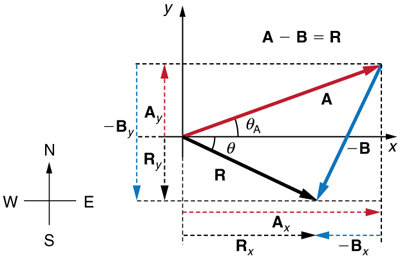
This example illustrates the addition of vectors using perpendicular components. Vector subtraction using perpendicular components is very similar—it is just the addition of a negative vector.
Subtraction of vectors is accomplished by the addition of a negative vector. That is, \displaystyle A−B≡A+(–B). Thus, the method for the subtraction of vectors using perpendicular components is identical to that for addition. The components of \displaystyle –B are the negatives of the components of \displaystyle B. The x- and y-components of the resultant \displaystyle A−B = R are thus
\displaystyle R_x=A_x+(–B_x)
and
\displaystyle R_y=A_y+(–B_y)
and the rest of the method outlined above is identical to that for addition. (See Figure \PageIndex{10}.)
Analyzing vectors using perpendicular components is very useful in many areas of physics, because perpendicular quantities are often independent of one another. The next module, Projectile Motion, is one of many in which using perpendicular components helps make the picture clear and simplifies the physics.
PHET EXPLORATIONS: VECTOR ADDITION
Learn how to add vectors. Drag vectors onto a graph, change their length and angle, and sum them together. The magnitude, angle, and components of each vector can be displayed in several formats.
- The analytical method of vector addition and subtraction involves using the Pythagorean theorem and trigonometric identities to determine the magnitude and direction of a resultant vector.
- The steps to add vectors \displaystyle A and \displaystyle B using the analytical method are as follows:
Step 1: Determine the coordinate system for the vectors. Then, determine the horizontal and vertical components of each vector using the equations
\displaystyle A_x=Acosθ
\displaystyle B_x=Bcosθ
and
\displaystyle A_y=Asinθ
\displaystyle B_y=Bsinθ.
Step 2: Add the horizontal and vertical components of each vector to determine the components Rx and Ry of the resultant vector, R:
\displaystyle R_x=A_x+B_x
and
\displaystyle R_y=A_y+B_y.
Step 3: Use the Pythagorean theorem to determine the magnitude, R, of the resultant vector R:
\displaystyle R=\sqrt{R^2_x+R^2_y}.
Step 4: Use a trigonometric identity to determine the direction, \displaystyle θ, of R:
\displaystyle θ=tan^{−1}(R_y/R_x).
Glossary
- analytical method
- the method of determining the magnitude and direction of a resultant vector using the Pythagorean theorem and trigonometric identities


