6.E: Work, Energy, and Energy Resources (Exercise)
- Last updated
- Jul 16, 2020
- Save as PDF
- Page ID
- 26531
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
7.1: Work: The Scientific Definition
1. Give an example of something we think of as work in everyday circumstances that is not work in the scientific sense. Is energy transferred or changed in form in your example? If so, explain how this is accomplished without doing work.
2. Give an example of a situation in which there is a force and a displacement, but the force does no work. Explain why it does no work.
3. Describe a situation in which a force is exerted for a long time but does no work. Explain.
7.2: Kinetic Energy and the Work-Energy Theorem
4. The person in Figure does work on the lawn mower. Under what conditions would the mower gain energy? Under what conditions would it lose energy?
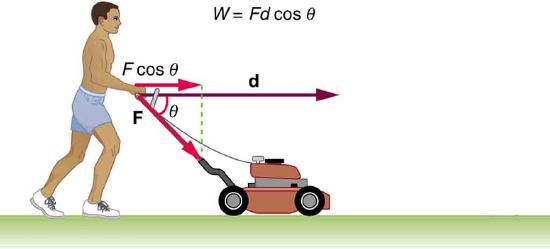
5. Work done on a system puts energy into it. Work done by a system removes energy from it. Give an example for each statement.
6. When solving for speed in Example, we kept only the positive root. Why?
7.3: Gravitational Potential Energy
7. In Example, we calculated the final speed of a roller coaster that descended 20 m in height and had an initial speed of 5 m/s downhill. Suppose the roller coaster had had an initial speed of 5 m/s uphill instead, and it coasted uphill, stopped, and then rolled back down to a final point 20 m below the start. We would find in that case that its final speed is the same as its initial speed. Explain in terms of conservation of energy.
8. Does the work you do on a book when you lift it onto a shelf depend on the path taken? On the time taken? On the height of the shelf? On the mass of the book?
7.4: Conservative Forces and Potential Energy
9. What is a conservative force?
10. The force exerted by a diving board is conservative, provided the internal friction is negligible. Assuming friction is negligible, describe changes in the potential energy of a diving board as a swimmer dives from it, starting just before the swimmer steps on the board until just after his feet leave it.
11. Define mechanical energy. What is the relationship of mechanical energy to nonconservative forces? What happens to mechanical energy if only conservative forces act?
12. What is the relationship of potential energy to conservative force?
7.6: Conservation of Energy
13. Consider the following scenario. A car for which friction is not negligible accelerates from rest down a hill, running out of gasoline after a short distance. The driver lets the car coast farther down the hill, then up and over a small crest. He then coasts down that hill into a gas station, where he brakes to a stop and fills the tank with gasoline. Identify the forms of energy the car has, and how they are changed and transferred in this series of events. (See Figure.)
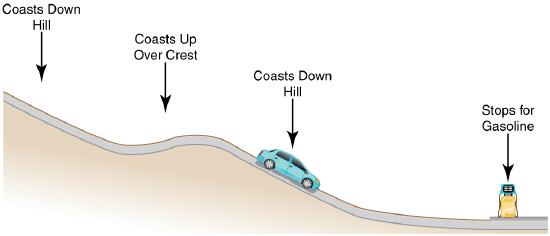
A car experiencing non-negligible friction coasts down a hill, over a small crest, then downhill again, and comes to a stop at a gas station.
14. Describe the energy transfers and transformations for a javelin, starting from the point at which an athlete picks up the javelin and ending when the javelin is stuck into the ground after being thrown.
15. Do devices with efficiencies of less than one violate the law of conservation of energy? Explain.
16. List four different forms or types of energy. Give one example of a conversion from each of these forms to another form.
17. List the energy conversions that occur when riding a bicycle.
7.7: Power
18. Most electrical appliances are rated in watts. Does this rating depend on how long the appliance is on? (When off, it is a zero-watt device.) Explain in terms of the definition of power.
19. Explain, in terms of the definition of power, why energy consumption is sometimes listed in kilowatt-hours rather than joules. What is the relationship between these two energy units?
20. A spark of static electricity, such as that you might receive from a doorknob on a cold dry day, may carry a few hundred watts of power. Explain why you are not injured by such a spark.
7.8: Work, Energy, and Power in Humans
21. Explain why it is easier to climb a mountain on a zigzag path rather than one straight up the side. Is your increase in gravitational potential energy the same in both cases? Is your energy consumption the same in both?
22. Do you do work on the outside world when you rub your hands together to warm them? What is the efficiency of this activity?
23. Shivering is an involuntary response to lowered body temperature. What is the efficiency of the body when shivering, and is this a desirable value?
24. Discuss the relative effectiveness of dieting and exercise in losing weight, noting that most athletic activities consume food energy at a rate of 400 to 500 W, while a single cup of yogurt can contain 1360 kJ (325 kcal). Specifically, is it likely that exercise alone will be sufficient to lose weight? You may wish to consider that regular exercise may increase the metabolic rate, whereas protracted dieting may reduce it.
7.9: World Energy Use
25. What is the difference between energy conservation and the law of conservation of energy? Give some examples of each.
26. If the efficiency of a coal-fired electrical generating plant is 35%, then what do we mean when we say that energy is a conserved quantity?
Problems & Exercises
7.1: Work: The Scientific Definition
27. How much work does a supermarket checkout attendant do on a can of soup he pushes 0.600 m horizontally with a force of 5.00 N? Express your answer in joules and kilocalories.
Solution
3.00J=7.17×10−4kcal
28. A 75.0-kg person climbs stairs, gaining 2.50 meters in height. Find the work done to accomplish this task.
29. (a) Calculate the work done on a 1500-kg elevator car by its cable to lift it 40.0 m at constant speed, assuming friction averages 100 N.
(b) What is the work done on the lift by the gravitational force in this process?
(c) What is the total work done on the lift?
Solution
(a) 5.92×105J
(b) −5.88×105J
(c) The net force is zero.
30. Suppose a car travels 108 km at a speed of 30.0 m/s, and uses 2.0 gal of gasoline. Only 30% of the gasoline goes into useful work by the force that keeps the car moving at constant speed despite friction. (See [link] for the energy content of gasoline.)
(a) What is the magnitude of the force exerted to keep the car moving at constant speed?
(b) If the required force is directly proportional to speed, how many gallons will be used to drive 108 km at a speed of 28.0 m/s?
31. Calculate the work done by an 85.0-kg man who pushes a crate 4.00 m up along a ramp that makes an angle of 20.0º with the horizontal. (See Figure.) He exerts a force of 500 N on the crate parallel to the ramp and moves at a constant speed. Be certain to include the work he does on the crate and on his body to get up the ramp.
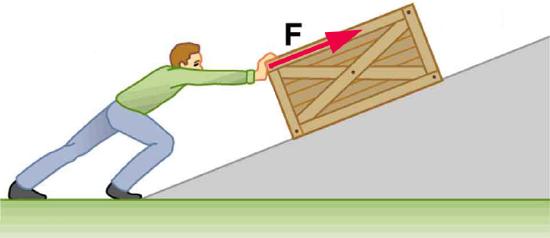
A man pushes a crate up a ramp.
Solution
3.14×103J
32. How much work is done by the boy pulling his sister 30.0 m in a wagon as shown in Figure? Assume no friction acts on the wagon.
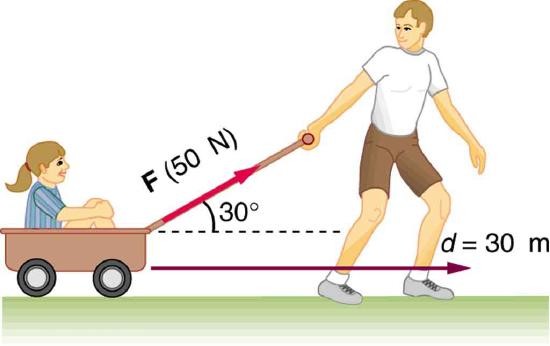
The boy does work on the system of the wagon and the child when he pulls them as shown.
33. A shopper pushes a grocery cart 20.0 m at constant speed on level ground, against a 35.0 N frictional force. He pushes in a direction 25.0º below the horizontal.
(a) What is the work done on the cart by friction?
(b) What is the work done on the cart by the gravitational force?
(c) What is the work done on the cart by the shopper?
(d) Find the force the shopper exerts, using energy considerations.
(e) What is the total work done on the cart?
Solution
(a) −700J
(b) 0
(c) 700 J
(d) 38.6 N
(e) 0
34. Suppose the ski patrol lowers a rescue sled and victim, having a total mass of 90.0 kg, down a 60.0º slope at constant speed, as shown in Figure. The coefficient of friction between the sled and the snow is 0.100.
(a) How much work is done by friction as the sled moves 30.0 m along the hill?
(b) How much work is done by the rope on the sled in this distance?
(c) What is the work done by the gravitational force on the sled?
(d) What is the total work done?
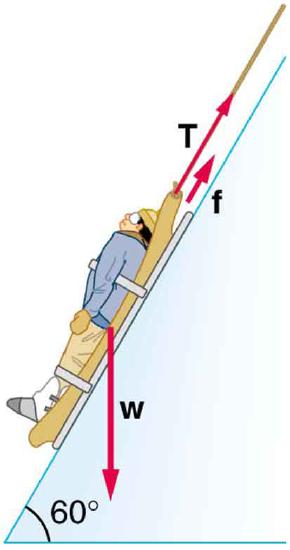
A rescue sled and victim are lowered down a steep slope.
7.2: Kinetic Energy and the Work-Energy Theorem
35. Compare the kinetic energy of a 20,000-kg truck moving at 110 km/h with that of an 80.0-kg astronaut in orbit moving at 27,500 km/h.
Solution
1/250
36. (a) How fast must a 3000-kg elephant move to have the same kinetic energy as a 65.0-kg sprinter running at 10.0 m/s?
(b) Discuss how the larger energies needed for the movement of larger animals would relate to metabolic rates.
37. Confirm the value given for the kinetic energy of an aircraft carrier in [link]. You will need to look up the definition of a nautical mile (1 knot = 1 nautical mile/h).
Solution
1.1×1010J
38. (a) Calculate the force needed to bring a 950-kg car to rest from a speed of 90.0 km/h in a distance of 120 m (a fairly typical distance for a non-panic stop).
(b) Suppose instead the car hits a concrete abutment at full speed and is brought to a stop in 2.00 m. Calculate the force exerted on the car and compare it with the force found in part (a).
39. A car’s bumper is designed to withstand a 4.0-km/h (1.1-m/s) collision with an immovable object without damage to the body of the car. The bumper cushions the shock by absorbing the force over a distance. Calculate the magnitude of the average force on a bumper that collapses 0.200 m while bringing a 900-kg car to rest from an initial speed of 1.1 m/s.
Solution
2.8×103N
40. Boxing gloves are padded to lessen the force of a blow.
(a) Calculate the force exerted by a boxing glove on an opponent’s face, if the glove and face compress 7.50 cm during a blow in which the 7.00-kg arm and glove are brought to rest from an initial speed of 10.0 m/s.
(b) Calculate the force exerted by an identical blow in the gory old days when no gloves were used and the knuckles and face would compress only 2.00 cm.
(c) Discuss the magnitude of the force with glove on. Does it seem high enough to cause damage even though it is lower than the force with no glove?
41. Using energy considerations, calculate the average force a 60.0-kg sprinter exerts backward on the track to accelerate from 2.00 to 8.00 m/s in a distance of 25.0 m, if he encounters a headwind that exerts an average force of 30.0 N against him.
Solution
102 N
7.3: Gravitational Potential Energy
42. A hydroelectric power facility (see Figure) converts the gravitational potential energy of water behind a dam to electric energy.
(a) What is the gravitational potential energy relative to the generators of a lake of volume 50.0km3(mass=5.00×1013kg), given that the lake has an average height of 40.0 m above the generators?
(b) Compare this with the energy stored in a 9-megaton fusion bomb.

Hydroelectric facility (credit: Denis Belevich, Wikimedia Commons)
Solution
(a) 1.96×1016J
(b) The ratio of gravitational potential energy in the lake to the energy stored in the bomb is 0.52. That is, the energy stored in the lake is approximately half that in a 9-megaton fusion bomb.
43. (a) How much gravitational potential energy (relative to the ground on which it is built) is stored in the Great Pyramid of Cheops, given that its mass is about 7×109kg and its center of mass is 36.5 m above the surrounding ground?
(b) How does this energy compare with the daily food intake of a person?
44. Suppose a 350-g kookaburra (a large kingfisher bird) picks up a 75-g snake and raises it 2.5 m from the ground to a branch.
(a) How much work did the bird do on the snake?
(b) How much work did it do to raise its own center of mass to the branch?
Solution
(a) 1.8 J
(b) 8.6 J
45. In Example, we found that the speed of a roller coaster that had descended 20.0 m was only slightly greater when it had an initial speed of 5.00 m/s than when it started from rest. This implies that \displaystyle ΔPE >> KE_i. Confirm this statement by taking the ratio of \displaystyle ΔPE to \displaystyle KE_i. (Note that mass cancels.)
46. A 100-g toy car is propelled by a compressed spring that starts it moving. The car follows the curved track in Figure. Show that the final speed of the toy car is 0.687 m/s if its initial speed is 2.00 m/s and it coasts up the frictionless slope, gaining 0.180 m in altitude.

A toy car moves up a sloped track. (credit: Leszek Leszczynski, Flickr)
Solution
\displaystyle v_f=\sqrt{2gh+v_0^2}=\sqrt{2(9.80 m/s^2)(−0.180 m)+(2.00 m/s)^2}=0.687 m/s
47. In a downhill ski race, surprisingly, little advantage is gained by getting a running start. (This is because the initial kinetic energy is small compared with the gain in gravitational potential energy on even small hills.) To demonstrate this, find the final speed and the time taken for a skier who skies 70.0 m along a \displaystyle 30º slope neglecting friction:
(a) Starting from rest.
(b) Starting with an initial speed of 2.50 m/s.
(c) Does the answer surprise you? Discuss why it is still advantageous to get a running start in very competitive events.
7.4: Conservative Forces and Potential Energy
48. A \displaystyle 5.00×10^5-kg subway train is brought to a stop from a speed of 0.500 m/s in 0.400 m by a large spring bumper at the end of its track. What is the force constant \displaystyle k of the spring?
Solution
\displaystyle 7.81×10^5N/m
49. A pogo stick has a spring with a force constant of \displaystyle 2.50×10^4N/m, which can be compressed 12.0 cm. To what maximum height can a child jump on the stick using only the energy in the spring, if the child and stick have a total mass of 40.0 kg? Explicitly show how you follow the steps in the Problem-Solving Strategies for Energy.
7.5: Nonconservative Forces
50. A 60.0-kg skier with an initial speed of 12.0 m/s coasts up a 2.50-m-high rise as shown in Figure. Find her final speed at the top, given that the coefficient of friction between her skis and the snow is 0.0800. (Hint: Find the distance traveled up the incline assuming a straight-line path as shown in the figure.)
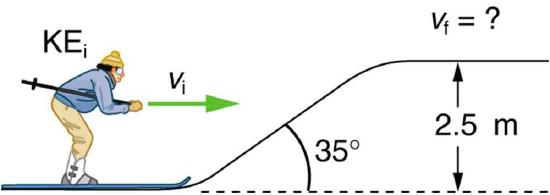
The skier’s initial kinetic energy is partially used in coasting to the top of a rise.
Solution
9.46 m/s
51. (a) How high a hill can a car coast up (engine disengaged) if work done by friction is negligible and its initial speed is 110 km/h?
(b) If, in actuality, a 750-kg car with an initial speed of 110 km/h is observed to coast up a hill to a height 22.0 m above its starting point, how much thermal energy was generated by friction?
(c) What is the average force of friction if the hill has a slope \displaystyle 2.5º above the horizontal?
7.6: Conservation of Energy
52. Using values from Table, how many DNA molecules could be broken by the energy carried by a single electron in the beam of an old-fashioned TV tube? (These electrons were not dangerous in themselves, but they did create dangerous x rays. Later model tube TVs had shielding that absorbed x rays before they escaped and exposed viewers.)
Solution
\displaystyle 4×10^4 molecules
53. Using energy considerations and assuming negligible air resistance, show that a rock thrown from a bridge 20.0 m above water with an initial speed of 15.0 m/s strikes the water with a speed of 24.8 m/s independent of the direction thrown.
Solution
Equating \displaystyle ΔPE_g and \displaystyle ΔKE, we obtain \displaystyle v=\sqrt{2gh+v_0^2}=\sqrt{2(9.80 m/s^2)(20.0 m)+(15.0 m/s)^2}=24.8 m/s
54. If the energy in fusion bombs were used to supply the energy needs of the world, how many of the 9-megaton variety would be needed for a year’s supply of energy (using data from Table)? This is not as far-fetched as it may sound—there are thousands of nuclear bombs, and their energy can be trapped in underground explosions and converted to electricity, as natural geothermal energy is.
55. (a) Use of hydrogen fusion to supply energy is a dream that may be realized in the next century. Fusion would be a relatively clean and almost limitless supply of energy, as can be seen from Table. To illustrate this, calculate how many years the present energy needs of the world could be supplied by one millionth of the oceans’ hydrogen fusion energy.
(b) How does this time compare with historically significant events, such as the duration of stable economic systems?
Solution
(a) \displaystyle 25×10^6years
(b) This is much, much longer than human time scales.
7.7: Power
56. The Crab Nebula (see Figure) pulsar is the remnant of a supernova that occurred in A.D. 1054. Using data from Table, calculate the approximate factor by which the power output of this astronomical object has declined since its explosion.

Crab Nebula (credit: ESO, via Wikimedia Commons)
Solution
\displaystyle 2×10^{−10}
57. Suppose a star 1000 times brighter than our Sun (that is, emitting 1000 times the power) suddenly goes supernova. Using data from Table:
(a) By what factor does its power output increase?
(b) How many times brighter than our entire Milky Way galaxy is the supernova?
(c) Based on your answers, discuss whether it should be possible to observe supernovas in distant galaxies. Note that there are on the order of \displaystyle 10^{11} observable galaxies, the average brightness of which is somewhat less than our own galaxy.
58. A person in good physical condition can put out 100 W of useful power for several hours at a stretch, perhaps by pedaling a mechanism that drives an electric generator. Neglecting any problems of generator efficiency and practical considerations such as resting time:
(a) How many people would it take to run a 4.00-kW electric clothes dryer?
(b) How many people would it take to replace a large electric power plant that generates 800 MW?
Solution
(a) 40
(b) 8 million
59. What is the cost of operating a 3.00-W electric clock for a year if the cost of electricity is $0.0900 per \displaystyle kW⋅h?
60. A large household air conditioner may consume 15.0 kW of power. What is the cost of operating this air conditioner 3.00 h per day for 30.0 d if the cost of electricity is $0.110 per \displaystyle kW⋅h?
Solution
$149
61. (a) What is the average power consumption in watts of an appliance that uses \displaystyle 5.00 kW⋅h of energy per day?
(b) How many joules of energy does this appliance consume in a year?
62. (a) What is the average useful power output of a person who does \displaystyle 6.00×10^6J of useful work in 8.00 h?
(b) Working at this rate, how long will it take this person to lift 2000 kg of bricks 1.50 m to a platform? (Work done to lift his body can be omitted because it is not considered useful output here.)
Solution
(a) 208 W
(b) 141 s
63. A 500-kg dragster accelerates from rest to a final speed of 110 m/s in 400 m (about a quarter of a mile) and encounters an average frictional force of 1200 N. What is its average power output in watts and horsepower if this takes 7.30 s?
64. (a) How long will it take an 850-kg car with a useful power output of 40.0 hp (1 hp = 746 W) to reach a speed of 15.0 m/s, neglecting friction? (b) How long will this acceleration take if the car also climbs a 3.00-m-high hill in the process?
Solution
(a) 3.20 s
(b) 4.04 s
65. (a) Find the useful power output of an elevator motor that lifts a 2500-kg load a height of 35.0 m in 12.0 s, if it also increases the speed from rest to 4.00 m/s. Note that the total mass of the counterbalanced system is 10,000 kg—so that only 2500 kg is raised in height, but the full 10,000 kg is accelerated.
(b) What does it cost, if electricity is $0.0900 per \displaystyle kW⋅h?
66. (a) What is the available energy content, in joules, of a battery that operates a 2.00-W electric clock for 18 months?
(b) How long can a battery that can supply \displaystyle 8.00×10^4J run a pocket calculator that consumes energy at the rate of \displaystyle 1.00×10^{−3}W?
Solution
(a) \displaystyle 9.46×10^7J
(b) \displaystyle 2.54 y
67. (a) How long would it take a \displaystyle 1.50×10^5-kg airplane with engines that produce 100 MW of power to reach a speed of 250 m/s and an altitude of 12.0 km if air resistance were negligible?
(b) If it actually takes 900 s, what is the power?
(c) Given this power, what is the average force of air resistance if the airplane takes 1200 s? (Hint: You must find the distance the plane travels in 1200 s assuming constant acceleration.)
68. Calculate the power output needed for a 950-kg car to climb a \displaystyle 2.00º slope at a constant 30.0 m/s while encountering wind resistance and friction totaling 600 N. Explicitly show how you follow the steps in the Problem-Solving Strategies for Energy.
Solution
Identify knowns: \displaystyle m=950 kg, slope angle\displaystyle θ=2.00º, v=3.00 m/s, f=600 N
Identify unknowns: power \displaystyle P of the car, force \displaystyle F that car applies to road
Solve for unknown:
\displaystyle P=\frac{W}{t}=\frac{Fd}{t}=F(\frac{d}{t})=Fv,
where \displaystyle F is parallel to the incline and must oppose the resistive forces and the force of gravity:
\displaystyle F=f+w=600 N+mgsinθ
Insert this into the expression for power and solve:
\displaystyle P=(f+mgsinθ)v
\displaystyle =[600 N+(950 kg)(9.80 m/s^2)sin 2º](30.0 m/s)
\displaystyle =2.77×10^4W
About 28 kW (or about 37 hp) is reasonable for a car to climb a gentle incline.
69. (a) Calculate the power per square meter reaching Earth’s upper atmosphere from the Sun. (Take the power output of the Sun to be \displaystyle 4.00×10^{26}W.)
(b) Part of this is absorbed and reflected by the atmosphere, so that a maximum of \displaystyle 1.30 kW/m^2 reaches Earth’s surface. Calculate the area in \displaystyle km^2 of solar energy collectors needed to replace an electric power plant that generates 750 MW if the collectors convert an average of 2.00% of the maximum power into electricity. (This small conversion efficiency is due to the devices themselves, and the fact that the sun is directly overhead only briefly.) With the same assumptions, what area would be needed to meet the United States’ energy needs \displaystyle (1.05×10^{20}J)? Australia’s energy needs \displaystyle (5.4×10^{18}J)? China’s energy needs \displaystyle (6.3×10^{19}J)? (These energy consumption values are from 2006.)
7.8: Work, Energy, and Power in Humans
70. (a) How long can you rapidly climb stairs (116/min) on the 93.0 kcal of energy in a 10.0-g pat of butter?
(b) How many flights is this if each flight has 16 stairs?
Solution
(a) 9.5 min
(b) 69 flights of stairs
71. (a) What is the power output in watts and horsepower of a 70.0-kg sprinter who accelerates from rest to 10.0 m/s in 3.00 s?
(b) Considering the amount of power generated, do you think a well-trained athlete could do this repetitively for long periods of time?
72. Calculate the power output in watts and horsepower of a shot-putter who takes 1.20 s to accelerate the 7.27-kg shot from rest to 14.0 m/s, while raising it 0.800 m. (Do not include the power produced to accelerate his body.)

Shot putter at the Dornoch Highland Gathering in 2007. (credit: John Haslam, Flickr)
Solution
641 W, 0.860 hp
73. (a) What is the efficiency of an out-of-condition professor who does \displaystyle 2.10×10^5 J of useful work while metabolizing 500 kcal of food energy?
(b) How many food calories would a well-conditioned athlete metabolize in doing the same work with an efficiency of 20%?
74. Energy that is not utilized for work or heat transfer is converted to the chemical energy of body fat containing about 39 kJ/g. How many grams of fat will you gain if you eat 10,000 kJ (about 2500 kcal) one day and do nothing but sit relaxed for 16.0 h and sleep for the other 8.00 h? Use data from Table for the energy consumption rates of these activities.
Solution
31 g
75. Using data from Table, calculate the daily energy needs of a person who sleeps for 7.00 h, walks for 2.00 h, attends classes for 4.00 h, cycles for 2.00 h, sits relaxed for 3.00 h, and studies for 6.00 h. (Studying consumes energy at the same rate as sitting in class.)
76. What is the efficiency of a subject on a treadmill who puts out work at the rate of 100 W while consuming oxygen at the rate of 2.00 L/min? (Hint: See Table.)
Solution
14.3%
77. Shoveling snow can be extremely taxing because the arms have such a low efficiency in this activity. Suppose a person shoveling a footpath metabolizes food at the rate of 800 W.
(a) What is her useful power output?
(b) How long will it take her to lift 3000 kg of snow 1.20 m? (This could be the amount of heavy snow on 20 m of footpath.)
(c) How much waste heat transfer in kilojoules will she generate in the process?
78. Very large forces are produced in joints when a person jumps from some height to the ground.
(a) Calculate the magnitude of the force produced if an 80.0-kg person jumps from a 0.600–m-high ledge and lands stiffly, compressing joint material 1.50 cm as a result. (Be certain to include the weight of the person.)
(b) In practice the knees bend almost involuntarily to help extend the distance over which you stop. Calculate the magnitude of the force produced if the stopping distance is 0.300 m.
(c) Compare both forces with the weight of the person.
Solution
(a) \displaystyle 3.21×10^4 N
(b) \displaystyle 2.35×10^3 N
(c) Ratio of net force to weight of person is 41.0 in part (a); 3.00 in part (b)
79. Jogging on hard surfaces with insufficiently padded shoes produces large forces in the feet and legs.
(a) Calculate the magnitude of the force needed to stop the downward motion of a jogger’s leg, if his leg has a mass of 13.0 kg, a speed of 6.00 m/s, and stops in a distance of 1.50 cm. (Be certain to include the weight of the 75.0-kg jogger’s body.)
(b) Compare this force with the weight of the jogger.
80. (a) Calculate the energy in kJ used by a 55.0-kg woman who does 50 deep knee bends in which her center of mass is lowered and raised 0.400 m. (She does work in both directions.) You may assume her efficiency is 20%.
(b) What is the average power consumption rate in watts if she does this in 3.00 min?
Solution
(a) 108 kJ
(b) 599 W
81. Kanellos Kanellopoulos flew 119 km from Crete to Santorini, Greece, on April 23, 1988, in the Daedalus 88, an aircraft powered by a bicycle-type drive mechanism (see Figure). His useful power output for the 234-min trip was about 350 W. Using the efficiency for cycling from [link], calculate the food energy in kilojoules he metabolized during the flight.

The Daedalus 88 in flight. (credit: NASA photo by Beasley)
82. The swimmer shown in Figure exerts an average horizontal backward force of 80.0 N with his arm during each 1.80 m long stroke.
(a) What is his work output in each stroke?
(b) Calculate the power output of his arms if he does 120 strokes per minute.
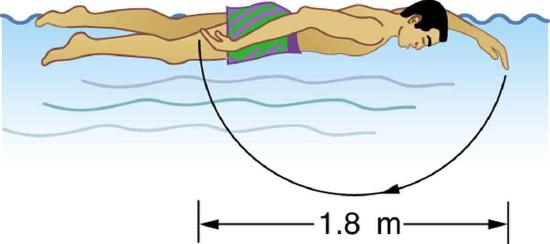
Solution
(a) 144 J
(b) 288 W
83. Mountain climbers carry bottled oxygen when at very high altitudes.
(a) Assuming that a mountain climber uses oxygen at twice the rate for climbing 116 stairs per minute (because of low air temperature and winds), calculate how many liters of oxygen a climber would need for 10.0 h of climbing. (These are liters at sea level.) Note that only 40% of the inhaled oxygen is utilized; the rest is exhaled.
(b) How much useful work does the climber do if he and his equipment have a mass of 90.0 kg and he gains 1000 m of altitude?
(c) What is his efficiency for the 10.0-h climb?
84. The awe-inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high, with a mass of about \displaystyle 7×10^9kg. (The pyramid’s dimensions are slightly different today due to quarrying and some sagging.) Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year.
(a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height.
(b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps (see Figure), bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 kcal/h. What does your answer imply about how much of their work went into block-lifting, versus how much work went into friction and lifting and lowering their own bodies?
(c) Calculate the mass of food that had to be supplied each day, assuming that the average worker required 3600 kcal per day and that their diet was 5% protein, 60% carbohydrate, and 35% fat. (These proportions neglect the mass of bulk and nondigestible materials consumed.)
Ancient pyramids were probably constructed using ramps as simple machines. (credit: Franck Monnier, Wikimedia Commons)
Solution
(a) \displaystyle 2.50×10^{12} J
(b) 2.52%
(c) \displaystyle 1.4×10^4 kg (14 metric tons)
85. (a) How long can you play tennis on the 800 kJ (about 200 kcal) of energy in a candy bar?
(b) Does this seem like a long time? Discuss why exercise is necessary but may not be sufficient to cause a person to lose weight.
7.9: World Energy Use
86. Integrated Concepts
(a) Calculate the force the woman in Figure exerts to do a push-up at constant speed, taking all data to be known to three digits.
(b) How much work does she do if her center of mass rises 0.240 m?
(c) What is her useful power output if she does 25 push-ups in 1 min? (Should work done lowering her body be included? See the discussion of useful work in Work, Energy, and Power in Humans.
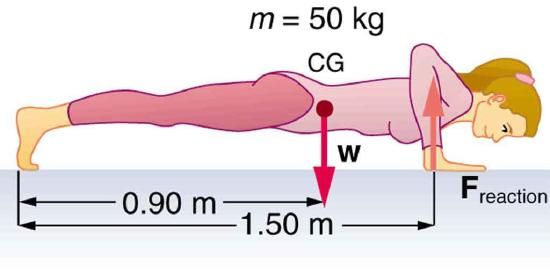
Forces involved in doing push-ups. The woman’s weight acts as a force exerted downward on her center of gravity (CG).
Solution
(a) 294 N
(b) 118 J
(c) 49.0 W
87. Integrated Concepts
A 75.0-kg cross-country skier is climbing a \displaystyle 3.0º slope at a constant speed of 2.00 m/s and encounters air resistance of 25.0 N. Find his power output for work done against the gravitational force and air resistance.
(b) What average force does he exert backward on the snow to accomplish this?
(c) If he continues to exert this force and to experience the same air resistance when he reaches a level area, how long will it take him to reach a velocity of 10.0 m/s?
88. Integrated Concepts
The 70.0-kg swimmer in [link] starts a race with an initial velocity of 1.25 m/s and exerts an average force of 80.0 N backward with his arms during each 1.80 m long stroke.
(a) What is his initial acceleration if water resistance is 45.0 N?
(b) What is the subsequent average resistance force from the water during the 5.00 s it takes him to reach his top velocity of 2.50 m/s?
(c) Discuss whether water resistance seems to increase linearly with velocity.
Solution
(a) \displaystyle 0.500 m/s^2
(b) \displaystyle 62.5 N
(c) Assuming the acceleration of the swimmer decreases linearly with time over the 5.00 s interval, the frictional force must therefore be increasing linearly with time, since \displaystyle f=F−ma. If the acceleration decreases linearly with time, the velocity will contain a term dependent on time squared (\displaystyle t^2). Therefore, the water resistance will not depend linearly on the velocity.
89. Integrated Concepts
A toy gun uses a spring with a force constant of 300 N/m to propel a 10.0-g steel ball. If the spring is compressed 7.00 cm and friction is negligible:
(a) How much force is needed to compress the spring?
(b) To what maximum height can the ball be shot?
(c) At what angles above the horizontal may a child aim to hit a target 3.00 m away at the same height as the gun?
(d) What is the gun’s maximum range on level ground?
90. Integrated Concepts
(a) What force must be supplied by an elevator cable to produce an acceleration of \displaystyle 0.800 m/s^2 against a 200-N frictional force, if the mass of the loaded elevator is 1500 kg?
(b) How much work is done by the cable in lifting the elevator 20.0 m?
(c) What is the final speed of the elevator if it starts from rest?
(d) How much work went into thermal energy?
Solution
(a) \displaystyle 16.1×10^3N
(b) \displaystyle 3.22×10^5J
(c) \displaystyle 5.66 m/s
(d) 4.00 kJ
91. Unreasonable Results
A car advertisement claims that its 900-kg car accelerated from rest to 30.0 m/s and drove 100 km, gaining 3.00 km in altitude, on 1.0 gal of gasoline. The average force of friction including air resistance was 700 N. Assume all values are known to three significant figures.
(a) Calculate the car’s efficiency.
(b) What is unreasonable about the result?
(c) Which premise is unreasonable, or which premises are inconsistent?
92. Unreasonable Results
Body fat is metabolized, supplying 9.30 kcal/g, when dietary intake is less than needed to fuel metabolism. The manufacturers of an exercise bicycle claim that you can lose 0.500 kg of fat per day by vigorously exercising for 2.00 h per day on their machine.
(a) How many kcal are supplied by the metabolization of 0.500 kg of fat?
(b) Calculate the kcal/min that you would have to utilize to metabolize fat at the rate of 0.500 kg in 2.00 h.
(c) What is unreasonable about the results?
(d) Which premise is unreasonable, or which premises are inconsistent?
Solution
(a) \displaystyle 4.65×10^3kcal
(b) 38.8 kcal/min
(c) This power output is higher than the highest value on [link], which is about 35 kcal/min (corresponding to 2415 watts) for sprinting.
(d) It would be impossible to maintain this power output for 2 hours (imagine sprinting for 2 hours!).
93. Construct Your Own Problem
Consider a person climbing and descending stairs. Construct a problem in which you calculate the long-term rate at which stairs can be climbed considering the mass of the person, his ability to generate power with his legs, and the height of a single stair step. Also consider why the same person can descend stairs at a faster rate for a nearly unlimited time in spite of the fact that very similar forces are exerted going down as going up. (This points to a fundamentally different process for descending versus climbing stairs.)
94. Construct Your Own Problem
Consider humans generating electricity by pedaling a device similar to a stationary bicycle. Construct a problem in which you determine the number of people it would take to replace a large electrical generation facility. Among the things to consider are the power output that is reasonable using the legs, rest time, and the need for electricity 24 hours per day. Discuss the practical implications of your results.
95. Integrated Concepts
A 105-kg basketball player crouches down 0.400 m while waiting to jump. After exerting a force on the floor through this 0.400 m, his feet leave the floor and his center of gravity rises 0.950 m above its normal standing erect position.
(a) Using energy considerations, calculate his velocity when he leaves the floor.
(b) What average force did he exert on the floor? (Do not neglect the force to support his weight as well as that to accelerate him.)
(c) What was his power output during the acceleration phase?
Solution
(a) 4.32 m/s
(b) \displaystyle 3.47×10^3N
(c) 8.93 kW
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

