7.3: Fluid Dynamics
- Last updated
- Nov 8, 2022
- Save as PDF
- Page ID
- 27792
( \newcommand{\kernel}{\mathrm{null}\,}\)
Steady-State
As with thermodynamics, fluids involve trillions of trillions of particles with freedom of movement, and also like thermodynamics, we would rather not treat them one particle at a time. One useful concept (which we have used previously but never discussed explicitly) is the concept of “steady-state.” We will find this idea to be extremely useful in our study of fluids, so we will take a closer look at what it means.
Consider the energy of a cannonball projectile.
Figure 7.2.1 – Before and After for a Single Cannonball

We know that energy is conserved for this cannonball as it flies through the air (we will ignore air resistance here), and we express this mathematically in terms of a zero change from "before" to "after."
ΔKE+ΔPE=0
Note especially that the Δ here means "after minus before," that is, it expresses a difference of quantities that are measured at different times.
Suppose now that cannonballs can be launched in rapid succession.
Figure 7.2.2 – Common Trajectory for Stream of Cannonballs

Of course they all follow the same trajectory, and this fact allows us to write down a new equation that looks identical to the one above, but has a different interpretation. In this case, we are not comparing the energies of a single cannonball at different times, but rather the energies of two different cannonballs at the same time. This leads us to a different type of model from what we used before. Previously we dealt with energy conservation from a before/after perspective, but with a steady flow, we are now able to use the concept of steady-state to make our comparisons at different positions rather than different times. Steady-state is a condition for flowing systems whereby the conditions at a fixed position remain constant in time. In other words, if you take a snap shot at two different times of the system as a whole, you would not be able to distinguish one snap shot from the other.
Assumptions: Incompressibility and Laminar Flow
As you might imagine, with particles in a fluid free to move around, it turns out that their motions can be very complicated. As with everything we study in physics, we need to make some simplifying assumptions so that we can reach some testable conclusions, and it is no different with fluid flow. We have already made one simplifying assumption in the previous section – we will treat fluids as though they are incompressible. Again, this means that we have to be very careful about applying these results to gases (though we can sometimes do so, at least approximately), but mostly the model we should keep in mind is that of a liquid.
The second simplifying assumption has to do with how the particles move relative to one another as they flow in steady-state. We will require that the flow of the fluid be laminar (also called streamline). Essentially what this means is that adjacent particles are, to a large degree, moving along parallel paths. When the flow gets too fast, or the shape of whatever is confining the motion of the flow changes too dramatically (actually, it is a combination of these things), then swirls and eddy currents arise, and turbulence ensues.
Figure 7.2.3 – Laminar vs. Turbulent Flow

The phenomenon of turbulence arises from effects that are non-linear, which makes it incredibly difficult to model and study. A non-linear phenomenon can loosely be described as one which feeds back on itself, and is therefore extremely sensitive to the conditions placed upon it. Most people are familiar with the unpredictability of weather patterns, and have perhaps heard of the famous "butterfly effect." This is an example of a non-linear system whose evolution is extremely sensitive to initial conditions. As important of a physics topic as turbulence is, we simply are not equipped to discuss it in any detail in this class ("not equipped" meaning we don't have a supercomputer to work with).
It should be noted that laminar flow does not assume that the inner walls of the vessel carrying the fluid are free of friction. For the flow to be streamline, the neighboring particles only have to move parallel to each other, they don’t have to move at the same speed. For a tube with friction against its inner surface, the particles will be moving slower than the particles near the center of the tube, but the flow is still streamline if they are moving parallel to each other.
Current, Volumetric Flow Rate, and Continuity
In fluid statics, the assumption of incompressibility was helpful in deriving a simple relationship between pressure and depth, because the density ρ remained constant throughout the fluid. In fluid dynamics, it has another interesting effect, when the vessel through which the fluid is flowing changes its cross-sectional area. Following a section of fluid through such a flow reveals:
Figure 7.2.4 – Incompressibility in a Bottleneck

With the fluid unable to compress, a given collection of particles in the fluid must morph their shape in the conduit such that their volume remains the same. This means that as the cross-sectional area of the conduit gets smaller, the volume of the fluid section we are tracking must get longer. That is:
V1=V2⇒A1Δx1=A2Δx2
Now we invoke our steady-state condition on this as follows: Let's wait a period of time equal to Δt, which is the amount of time it takes all the fluid that is initially within volume V1 (the wide, short, red cylinder in the diagram above) to exit that volume. It should be clear from the fact that this is operating at steady-state that in this same period of time, all the fluid in volume V2 (the thin, long, red cylinder in the diagram above) has just enough time to exit that volume. The speed of the flow through each volume is the distance the fluid at the rear of the cylinder must travel to get to the front of the cylinder, divided by the time required, so we can relate the velocities of the fluid at the two points in question:
The value of each side of this equation is the rate at which volume of fluid is passing a fixed point. This is commonly referred to as volumetric flow rate, or more generically as current (which technically can be any kind of flow rate, not just volume), and can be written as:
I=dVdt=Av
What Equation 7.3.3 tells us is that for an incompressible fluid, the volumetric flow rate is the same everywhere in the fluid. This relation is referred to as the equation of continuity, which can be alternatively expressed as:
I=dVdt=Av=constantthroughoutthefluid
This expresses a conservation principle of sorts – all the fluid that comes into a given region in a given period of time also passes out of that region in the same period of time – there is no build-up or loss of fluid in that region.
Energy Density
In studying the dynamics of fluids, we seek to describe mathematically how the various physical properties of a moving fluid are related to each other. Judging from our study of fluid statics, there are already a number of properties that we know must play a role:
- the density of the fluid, ρ
- the height at some position in the fluid, y
- the pressure at some position in the fluid, P
Now that we are dealing with dynamics, we need to add this to the list:
- the speed of the fluid at some position, v
Whatever relationship we find between these quantities must reduce to what we found previously in our discussion of statics, when we set the speed equal to zero.
We are not worried about directions here, so a complicated vector analysis is (thankfully) unnecessary. We therefore turn to energy conservation. We also will make use of our steady-state condition, which means that our energy conservation equation will involve a comparison of two different positions in a continuous fluid, rather than the fate of a single sample of fluid at two different times. This will certainly fit nicely with our study of fluid statics, where we also compared properties of a continuous fluid at different places.
There is one problem we need to overcome in our application of energy conservation, however. What energies are we comparing? Each particle in the fluid has some amount of energy, but there is a degree of randomness to their motions, so two particles that are side-by-side in the fluid do not necessarily have the same energy. Really what we want is to compare the average energies of particles. To do this, we need to compare energies of a collection of particles. Suppose we take a tiny sampling of the energies of particles at two different positions in a fluid:
Figure 7.2.5 – Sampling Small Volumes of Particles in a Fluid
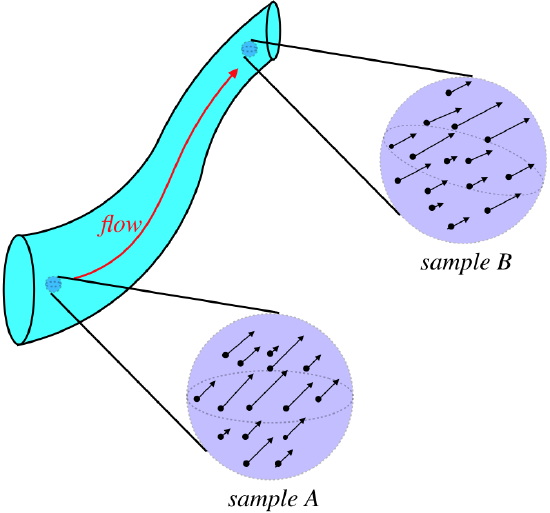
The average energy per particle in each of these samplings is found by adding up their individual energies and dividing by the number of particles:
⟨E⟩=(KE1+PE1)+(KE2+PE2)+…N
Assuming no work is done on the particles from position A to position B by forces other than those accounted-for in the potential energy, these averages should be equal for each sample. The number of particles is difficult to work with, so we note that we are assuming that this fluid is incompressible, which tells us that the particle density is the same everywhere in the fluid. So rather than use the average energy per particle as a basis for comparison, we can use the average energy per volume:
(KE1+PE1)+(KE2+PE2)+…V=⟨E⟩NV
We call this the average energy density of the fluid for the sample selected. We want to study the fluid at a specific position, so we need to make our sample volume smaller and smaller. As we do so, the energy contained therein also gets smaller and smaller, but the ratio of energy and volume converges to the energy density at that position:
E=lim
We can break this energy density into the kinetic and potential parts. We'll start with kinetic...
When the focus is narrowed down to a single point (i.e. the volume goes to the zero limit), the average speed of the fluid doesn't change, but with the constant density, the mass gets ever smaller. We have, therefore, that the kinetic energy density is written in terms of the mass density and speed:
The only potential energy we will be dealing with here is gravitational. Once again, we see that only the mass gets small in the limit as the volume vanishes, that is, the height doesn't change. so we have:
\dfrac{d\left(PE\right)}{dV} =\dfrac{d}{dV}\left(mgy\right) = \dfrac{dm}{dV}gy =\rho gy
So the full mechanical energy density is:
\mathcal E = \frac{1}{2}\rho v^2 + \rho gy
Energy Conservation
So now we have a way of comparing energy at different positions in a fluid – we compare the energy densities at those points. Before we just launch into invoking energy conservation, there is one thing we need to address. Above we made the qualification, "Assuming no work is done on the particles from position A to position B by forces other than those accounted-for in the potential energy..." Are there any forces present that could be responsible for work like this? Well, there could be friction along the walls of the vessel, but in true Physics 9 fashion, we will treat this as negligible. There is, however, one source of work that we can't ignore.
We saw in the case of static fluids that the pressure can vary from one place to the other. Now that the fluid can move, if the pressure in front of a moving segment of fluid is different from the pressure behind it, the net force created by the difference in the pressures can do work. We therefore need to include the work done by pressure differences in our energy conservation calculations. Fortunately, from our work in thermodynamics, we are already familiar with how to compute work done by pressure:
dW = PdV
The difference in this case is that the work done is not acting to compress or expand a gas – the volume change in this case is just the displacement of an incompressible segment of fluid. The picture we have then is of a fluid passing through a conduit which in general changes heights and cross-sectional areas. Because we are more comfortable dealing with energy conservation from a before/after perspective, we'll start with that, then invoke steady state to extend our conclusions to compare different positions in the fluid.
Figure 7.2.6a – Fluid Flow Through a Pipe
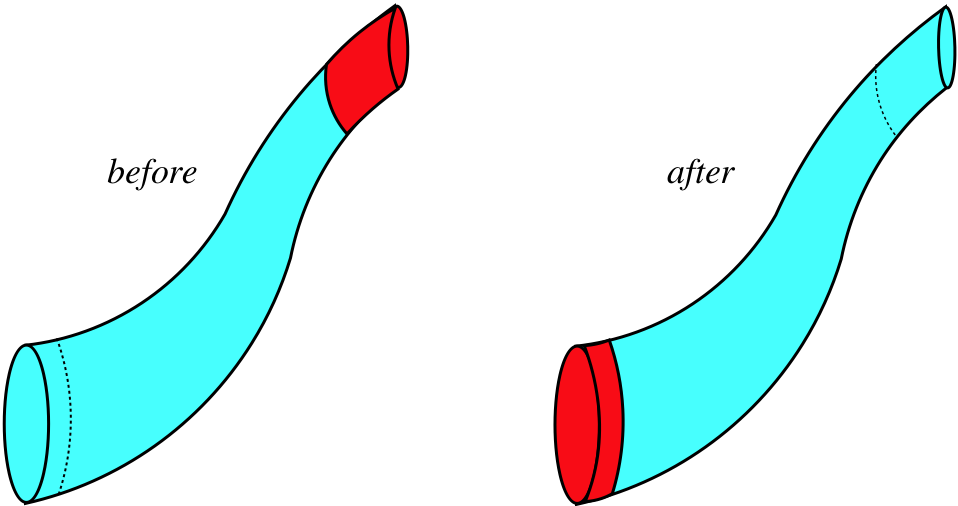
The fluid we are watching here is blue. The red sections also contain fluid, but we are confining ourselves to watching what happens to the blue segment of fluid. In the time between "before" and "after," the fluid flows up through the pipe, and the same amount of fluid that vacates the bottom portion of the pipe (turning that section red) fills in the top portion of the pipe (turning it from red to blue).
This blue segment of fluid is experiencing a force due to the adjacent fluid, so the bottom face of the blue segment of fluid experiences a force in the direction of motion of the fluid segment, while the top face of the blue segment of fluid experiences a force opposing its motion. The total work done on the blue segment of fluid is is therefore:
dW = P_{bottom}dV_{bottom} - P_{top}dV_{top}
The fluid is incompressible, which means that the volumes for top and bottom (represented by the red region) are equal to each other, which tells us that the work done on this segment of fluid is:
dW=\left(P_{bottom} - P_{top}\right)dV
Now we are ready to invoke energy conservation. The work done on the system equals the change in its mechanical energy, which is a change from one small quantity to another (both top and bottom involve a tiny volume), so:
dW = d\left(KE_{top}\right)-d\left(KE_{bottom}\right) + d\left(PE_{top}\right) - d\left(PE_{bottom}\right)
Dividing every term in this equation by dV and plugging in Equations 7.3.9, 7.3.10, and 7.3.14 gives:
P_{bottom} - P_{top} =\frac{1}{2}\rho \left(v_{top}^2-v_{bottom}^2\right) + \rho g\left(y_{top}-y_{bottom}\right)
We can write this result (called Bernoulli's equation) two ways, as with our usual energy conservation principle:
\begin{array}{l} \Delta P + \frac{1}{2}\rho\Delta\left(v^2\right) + \rho g \Delta y = 0 \\ P_1 + \frac{1}{2}\rho v_1^2 + \rho g y_1 = P_2 + \frac{1}{2}\rho v_2^2 + \rho g y_2 \end{array}
Figure 7.2.6b – Fluid Flow Through a Pipe

Note that although we derived this using a "before/after" approach, the \Delta refers to a difference in positions, in keeping with the steady-state assumption.
Recall we wanted to check the result we got in fluid statics against this result for v=0. Sure enough, if we put in v_1=v_2=0, we get back to Equation 7.1.2.
Example \PageIndex{1}
Air flows from left to right through a horizontal pipe that has different diameters in two different sections, as shown in the diagram. The narrow section has a radius of 5.0\;cm, and the wider section has a radius of 20\;cm. At point 1, the air is flowing with a velocity of 10\;m/s, and has an absolute pressure of 150,000\;Pa. A narrow U-shaped tube has been attached to the air tube, and this U-shaped tube is filled with water. Note that no air actually flows into or out of the U-shaped tube, but instead flows right across its openings. The pressures at points 1 and 2 are different, so the water in the U-shaped tube is not level. Assume that the transitions between the sections have a negligible effect on the frictionless flow of air, and that the density of air is a constant 1.2\frac{kg}{m^3} throughout the pipe. Also, despite how the diagram looks, assume that the difference in height of the connection points of both ends of the U-shaped tube is negligible.

- Find the speed of the air and its pressure at point 2.
- Find the difference in heights (\Delta y) of the water in the U-shaped tube.
- Solution
-
a. We can apply Bernoulli’s equation to the moving air in the pipe and in the U-shaped tube, but we must do so separately, since they are two separate fluid systems. In order to work out \Delta y, we need to know the pressure difference at the two ends of the U-shaped tube, which means we have to work out the air flow part first. Start by finding the speed of the air at point 2, using the continuity equation (Equation 7.3.3):
A_1v_1 = A_2v_2\;\;\;\Rightarrow\;\;\;v_2 = \dfrac{A_1}{A_2}v_1 = \dfrac{\pi r_1^2}{\pi r_2^2}v_1 = \dfrac{\left(20cm\right)^2}{\left(5.0cm\right)^2}\left(10\frac{m}{s}\right) = 6.25\frac{m}{s} \nonumber
Applying Bernoulli's equation with no change in height gives us the pressure at point 2:
\Delta P + \frac{1}{2}\rho\Delta\left(v^2\right) + 0\;\;\;\Rightarrow\;\;\; P_2 = P_1 +\frac{1}{2}\rho\left(v_1^2-v_2^2\right)=150,000Pa + \frac{1}{2}\left(1.2\frac{kg}{m^3}\right)\left[\left(10\frac{m}{s}\right)^2-\left(0.625\frac{m}{s}\right)^2\right]=150,060Pa\nonumber
b. The difference in pressures at the two ends of the U-shaped tube is 60\;Pa, and this determines the difference in heights of the columns of water. The water in these tubes is not moving, so we can plug in zero for the velocities (or equivalently, just use the fluid statics formula):
\Delta P + 0 + \rho g \Delta y = 0 \;\;\;\Rightarrow\;\;\; \left|\Delta y\right| = \left|\dfrac{\Delta P}{\rho g}\right| = \dfrac{60Pa}{\left(1000\frac{kg}{m^3}\right)\left(9.8\frac{m}{s^2}\right)} = 0.61cm\nonumber




