7.1: Static Fluids
- Last updated
- Nov 8, 2022
- Save as PDF
- Page ID
- 27790
( \newcommand{\kernel}{\mathrm{null}\,}\)
Pressure in Static Fluids
A fluid is a collection of matter that is not a solid. That is, the particles that comprise the matter are not strongly bound to each other in a fixed lattice. This includes the liquid, gaseous, and even plasma states of matter. We will actually need to restrict the properties of the fluids we examine to some extent, so that we can get some approximate results, but the usefulness of the applications of these models cannot be overstated.
A key property in all fluids is pressure. We have discussed this at length in the context of gases in thermodynamic equilibrium, but in the context of fluids, we need to loosen the restrictions we previously placed on this quantity. The main difference is that unlike gases at equilibrium, where we assumed that the pressure was a state variable that was the same in every cubic centimeter of a volume of gas at equilibrium, now we will allow the pressure to vary from one position to the next within a fluid. [In truth, having a pressure that varies with position within a gas also lies in the purview of thermodynamics, though we did not delve sufficiently deeply into the subject to discuss it.]
Consider a container of fluid in a gravitational field. If we draw a free-body diagram for a small section of that fluid (and exclude the horizontal forces), then three forces come to mind: The force of gravity on that section, the amount that the fluid above that section pushes down on it, and the amount that the fluid below that section pushes up on it. This diagram is really no different from one we would draw for a book in the middle of a stack of books.
Figure 7.1.1 – Free-Body Diagram for a Section of Fluid

The question is, how exactly does one region of fluid exert a force on another? Truthfully, it does not. Particles in one region are changing places with particles in the other region all the time. Also, as we know, if this fluid happens to be an ideal gas, then the particles aren't even interacting with each other. However, if we were to place a membrane between two regions, then particle reflections off the membrane would result in a force, and the resulting physics would be the same – the segment of fluid does not accelerate up or down. We therefore take the view that although over time it is not actually the same particles enclosed within the small volume, it behaves in precisely the same way as if we could somehow confine them to that volume, and our force analysis is valid.
As we first discussed in Section 5.5, we can express this particle-reflects-off-surface force in terms of a property of the fluid that we call pressure. The forces from the fluid above and below is therefore equal to the pressures of the fluid above and below multiplied by the cross-sectional areas, and the zero net force from the FBD gives:
Ffluidabove=PaboveAFfluidbelow=PbelowA}⇒PbelowA=PaboveA+mg
As we can readily see, the pressure varies with position in a fluid (namely, at differing heights) in the presence of gravity, even though the fluid is in equilibrium. Perhaps the reader is wondering how we got away with ignoring this effect in our study of thermodynamics. A sample calculation will answer this question.
Example 7.1.1
Compute the pressure difference between the top and bottom of a volume of 1 mole of diatomic nitrogen at 300K at atmospheric pressure (101kPa) confined to a cubical container.
- Solution
-
Start by treating the gas as ideal and compute the volume:
V=nRTP=(1mol)(8.31JmolK)(300K)1.01×105Pa=0.0247m3
The container is cubical, so from the volume we can determine the length of each side, which gives us the cross-sectional area:
L=V13=0.291m⇒A=0.0848m2
The molecular mass of N2 is 28.0, so the mass of the enclosed gas is 28.0g. This means that the weight of the gas enclosed is:
Wgas=mg=(0.028kg)(9.8ms2)=0.274N
This weight, divided by the horizontal cross-sectional area equals the difference in pressure between the top and bottom:
ΔP=0.274N0.0848m2=3.23Pa
When measured against the average pressure of ≈105Pa, this difference is easily negligible.
Given that we need very large height differences to start seeing significant pressure differences in gases, we will primarily be dealing with liquid fluids from this point forward. More importantly, considering only liquids takes away another troublesome complication that exists for gases – liquids are largely incompressible. This means that we don't have to worry about the effect that increased pressure has on the mass density of the liquid – an important quantity, as we will see next.
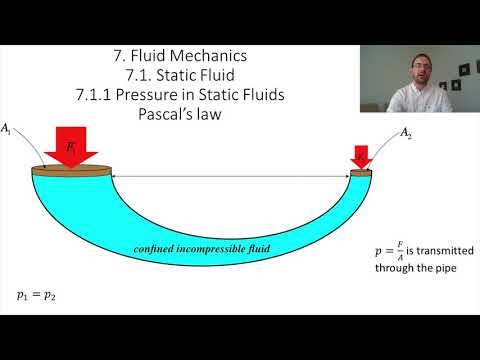
Pascal's Law
We can rearrange things in Equation 7.1.1 so that the pressure difference between two heights in the fluid are related to the mass density (ρ, mass per unit volume) of the fluid:
Pbelow=Pabove+mgΔyAΔy=Pabove+mgΔyV=Pabove+ρgΔy
The nice thing about this result is that it directly compares two pressures, and doesn't rely upon a choice of a particular disk of fluid for our free-body diagram. This means that if we choose a disk that has less cross-sectional area (but with the same thickness), we find the same difference in pressure. In other words, it turns out that the pressure difference at two depths only depends upon the density of the fluid and the difference in height between the two depths.
Just how robust is this conclusion? For example, suppose we have a fluid confined to a container like the one shown in the figure below. Is the pressure difference between the two heights indicated the same on both sides of the container?
Figure 7.1.2 – Comparing Pressures in Different Parts of a Continuous Fluid

Well, naturally the same analysis applies to both sides of this container, so the pressure difference is the same on both sides, but are they the same two pressures on both sides? Here we need to invoke the principal that pressure does not have a direction. That is, whatever the pressure is at the bottom of Δy, that results in a force pushing up on the section of fluid, it also results in a force pushing on a segment of fluid to the side of the position in question. That lateral segment is static just like the remainder of the fluid, so the pressure on both sides must be equal, which means that the pressure is the same everywhere along the lower dashed line.
We already concluded that the pressure difference between the two dashed lines is the same in both columns of fluid, so since the pressures are the same in both columns at the bottom line, they are also the same at the top line. We therefore conclude Pascal's law:
The pressures measured at all points at the same height in a continuous static fluid are equal.
Alert
It is important to make a note of all the qualifiers in Pascal's law. Besides being at equal heights, the fluid must be static – later we will get a slightly more complicated result when the fluid is moving. Also, the fluid must be continuous – if a solid barrier cuts one section off completely from the other, then the requirement that pressure is the same horizontally no longer holds. Another way for the fluid to not be "continuous" is for the fluid's density to not be the same everywhere. So two unmixed fluids in contact will result in the density changing across the boundary of the two fluids, and we cannot conclude that pressures at the same height within the different fluids are equal.
The Hydraulic Lift
The result we obtained above compares the pressure at any two points in the fluid, but by far the most common comparison is between the pressure at the top surface of the fluid and the pressure at some depth below that surface. Calling the pressure at the surface Po and the depth below that surface d, Equation 7.1.2 becomes:
P(d)=Po+ρgd
Digression: Rule of Thumb for Water
With the density of liquid water equal to 1000kgm3, atmospheric pressure at sea level equal to about 105Nm2, and the constant g approximately equal to 10ms2, it's easy to compute approximately how fast the pressure rises with depth under water – the pressure increases by an amount of one atmosphere with every 10m of added depth.
The salt water of the oceans is slightly denser than fresh water, so the pressure goes up slightly faster than this, and all certified scuba divers that use the English system of units are aware that one atmosphere of pressure is gained for every 33 feet of added depth. At the deepest point in the ocean, this amounts to a pressure of almost 1100 atmospheres!
The top surface of the fluid may just be exposed to the atmosphere, in which case Po is simply 101kPa (at sea level). But the fluid could also be confined by a piston, which leads to an interesting application called a hydraulic lift. The idea is to confine the liquid with pistons of different areas on opposite ends of a continuous fluid, as shown in the following figure.
Figure 7.1.3 – Balancing Forces on a Hydraulic Lift

With the bottom surfaces of the two pistons in contact with the same continuous fluid at the same height, the pressure of the fluid is the same at both surfaces. The forces exerted by the fluid on the two pistons are not the same, however, because the areas are not equal. With pressures equal at both ends, the fluid exerts more force on the piston with a larger area, which means a heavier weight on the larger piston is balanced by a lighter weight on the other piston. This allows for a mechanical advantage in lifting a heavy weight with far less force than the weight, determined by the ratio of the piston areas:
P1=P2⇒F1A1=F2A2⇒F1F2=A1A2
Manometers
Pascal's law also gives us a way to measure unknown pressures by comparing them to known values. A generic device of this kind is called a manometer. There are many specialized devices designed to measure specific pressures, such as a barometer (which measures the pressure of the atmosphere), and a sphygmomanometer (which measures blood pressure).
The simplest designs for manometers involve exposing one end of a continuous confined liquid to the region for which the pressure is to be measured, and the other end to a vacuum (i.e. a region where the pressure is effectively zero), then measure the difference in height of the two columns of the liquid and use the liquid's known density to compute the pressure difference. For example, here is a simple barometer:
Figure 7.1.4 – A Simple Barometer

In the figure above, the fluid is exposed to the atmosphere in the large tub, and the top of the vertical tube is evacuated. This is most easily achieved by filling the tube with the fluid, covering the open end, inverting it in the tube, then uncovering the open end so that the fluid runs out until equilibrium is reached. [Technically this does not result in an actual vacuum, as the particles in the liquid will leave the surface to go into vapor to fill this region, but this vapor pressure is very small compared to atmospheric pressure (less than 4% of atmospheric pressure at 300K).]
Applying Pascal's law, the pressure of the atmosphere at the exposed surface is the same as within the column at the same height, and applying our equation for pressure at depth, we have:
Patm=Po+ρgd=ρgd
Thus we can measure the pressure of the atmosphere by measuring the height of the column of fluid and knowing its density. Note that this means that there is a maximum height to which we can raise this column by evacuating the space above it, and it points out an important common misconception. It is commonly believed that "suction" is an attractive force – that the more suction a pump can apply, the more it can "draw" a fluid. Here we see that all "suction" does is remove the pushing force due to one source of pressure, allowing the force exerted due to a pressure elsewhere to act unbalanced.
Plugging in the density of water and atmospheric pressure at sea level, we find that the farthest a column of water can be held up with a vacuum is a bit over 10m. If we wish to pump water out of a well (or to a higher floor of a building), we can't "draw it up" by creating a vacuum above it from any depth greater than that. The approach that is therefore used instead is to pump the bottom of the column of water to increase its pressure. The only limit to depth from which the water can be extracted in this case is in the horsepower of the motor driving the pump.
Assuming we are working with pressures in the vicinity of an atmosphere, using water makes for a pretty tall manometer! The way to bring down this column size is to use a fluid that is more dense. The substance that is a liquid at room temperature and has the greatest density is mercury, and so ubiquitous was its use many years ago, that a unit of measurement for pressure was based on it. It turns out that 1 atmosphere will only support a column of Hg that is 760mm high. One atmosphere of pressure is therefore expressed in alternative units as "760mmHg" or "760Torr."
Here is a simple design for a simple gas pressure manometer (i.e. for enclosed gases of any variety, not just the atmosphere):
Figure 7.1.5 – A Simple Manometer

When the pressure is measured in this manner, we say that it is the absolute pressure that is measured. It seems silly to add the unnecessary extra word "absolute," but there is a practical reason for this. When it comes to gauges that measure pressure of gases in industrial applications, what the operator of a machine wants to know is if the pressure is close to exceeding the capacity of the device confining the gas. Well, any pressure acting from outside the device is helping to keep it from exploding, so what is needed is the pressure difference between the trapped gas and what is outside. We can measure this directly using the device above by opening the top of the tube so that there is no longer a vacuum there. Then the column height measures the difference between the trapped gas and the ambient pressure. This measurement of pressure is called gauge pressure. There is an analogy here with temperature – absolute temperature is measured on the kelvin scale, and zero is as low as it can go. The celsius scale has the same grading as kelvins, but puts the zero point at the freezing point of water, thus allowing for negative values. Similarly, gauge pressure places the zero point at the ambient (typically atmospheric) pressure, also allowing for a negative value of the pressure measurement.
Example 7.1.2
A U-shaped glass tube of constant cross-sectional area and two right angles has a base that is 36cm long, and is open to the air at both ends, as shown in the figure below. Some water is poured into this tube, and it just exactly fills the bottom, horizontal part of the tube. An equal volume of oil with a density of 0.80gcm3 is then slowly added to one side of the tube, such that the oil and water remain unmixed, in contact at a single point in the tube.

- Find the distance from the contact point of the oil and water to the center of the glass tube.
- The end of the tube with the water is connected to a confined volume of gas at an unknown pressure, and the contact point of the oil and water moves to the center of the tube. Find the gauge pressure of the gas.
- Solution
-
a. The contact point of the oil and water is a point where the pressure of the oil equals the pressure of the water (otherwise one would displace the other). Assuming this point of contact is somewhere in the bottom section of the tube (and it has to be, since the oil can't simply come in contact with the water without pushing it at least a little bit up the other side), the pressure for the oil an water are each related to how high their columns go up their respective sides:
Pwater=Patm+ρwaterghwaterPoil=Patm+ρoilghoil}Pwater=Poil⇒Patm+ρwaterghwater=Patm+ρoilghoil⇒hoil=ρwaterρoilhwater
The density of water is 1.0gcm3, so the ratio of the height of the oil column to the water column is 54. The liquids are incompressible, so since there are equal volumes of oil and water, the total length of the two columns must be 36cm, which gives us a second equation, allowing us to solve for the heights of the two columns:
hoil=54hwaterhoil+hwater=36cm}⇒hoil=20cm,hwater=16cm
With the top of the column of oil 4cm higher than the top of the column of water, the contact point of the oil and water must be offset from the center by 2cm.
b. With the contact point centered in the bottom section of the tube, the columns of water and oil are equal heights. Once again, the pressures of the fluids at the contact point are equal, but the pressures at the tops of the columns are not. The gauge pressure is the difference between the pressure of the gas and the atmosphere, so:
Pwater=Pgas+ρwaterghPoil=Patm+ρoilgh}Pwater=Poil⇒Pgauge=Pgas−Patm=(ρoil−ρwater)gh=(−200kgm3)(9.8ms2)(0.18m)=−353Pa
The gauge pressure is negative, which means the gas pressure is lower than atmospheric pressure.