2.5: Surface Tension and Line Tension
- Page ID
- 1984
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Cell membranes are composed of phospholipids (most abundant), proteins, and glycolipids (Figure 1)1,2. Generally, phospholipids in cell membranes will aggregate together in order to maximize hydrophobic interactions among their tails and hydrophilic interactions among their heads. Any in-plane stretching of cell membrane will disrupt the interaction between phospholipids. However, in-plane membrane tension (Tm), which is the force needed to stretch the membrane, will counteract any membrane deformation3. Tm, which seems to be constant across the whole cell membrane4, depends on lipid composition and surface area of the cell membrane. Without changing the amount of lipid, increasing the surface area of cell membrane will increase membrane tension5. For example, cells will swell when they are in a hypotonic environment. Cell swelling will cause an increase in cell membrane surface area without changing the the amount of lipid in the membrane. In addition, cell membranes are connected to a cross-linked actin network named the cortex6. The cortex is demonstrated as a purple mesh under the membrane in Figure 1. Actin cytoskeleton supports cell membrane and helps cells maintain their shape6. Membrane surface tension, which consist of Tm and membrane-cytoskeleton adhesion, is the cohesive force that keep cell membranes intact. In order to deform cell membrane, you need to overcome both Tm and membrane-cytoskeleton adhesion3,4. Membrane surface tension helps cell maintain a small surface area.

As shown in Figure 1, cell membranes consist of various types of lipid (e. g. cholesterol, saturated/unsaturated phospholipids, and glycosylated lipids)2. Interactions between lipids in the membrane lead to formation of ordered membrane regions that recruit other lipids and proteins2. Consequently, there is a wide variety membrane domains with different molecular composition and properties7. In addition, lateral segregation of lipids leads to phase separations within cell membranes. Phase separation within cell membrane depends on temperature, pressure, and structural properties (e. g. hydrocarbon tails length or degrees of unsaturation, and the composition of the head group) of various lipid within the membrane1. For more info, refer to the wiki pages for Phase Coexistence and Membrane Phase Transitions. At the edge of membrane domains or at the lipid phase separations, phospholipid height mismatch and steric interactions have an energetic cost that depends on the length of the phase/domain boundary8. Line tension is the interfacial energy at the edge of membrane domain or at the lipid phase separation in cell membrane9. In order to minimize line tension, membrane domains tend to assume circular shapes (Figure 2)9. The free energy penalty associated with the line tension is compensated by the decrease in free energy due to membrane domain formations. Membrane tension plays important role in many biological processes, such as cell motility, endocytosis/exocytosis, and viral infection. Many techniques, such as atomic force microscopy (AFM) and micropipette aspiration, are used to study membrane tension.

Biological Relevance
Membrane Tension and Cell Movement
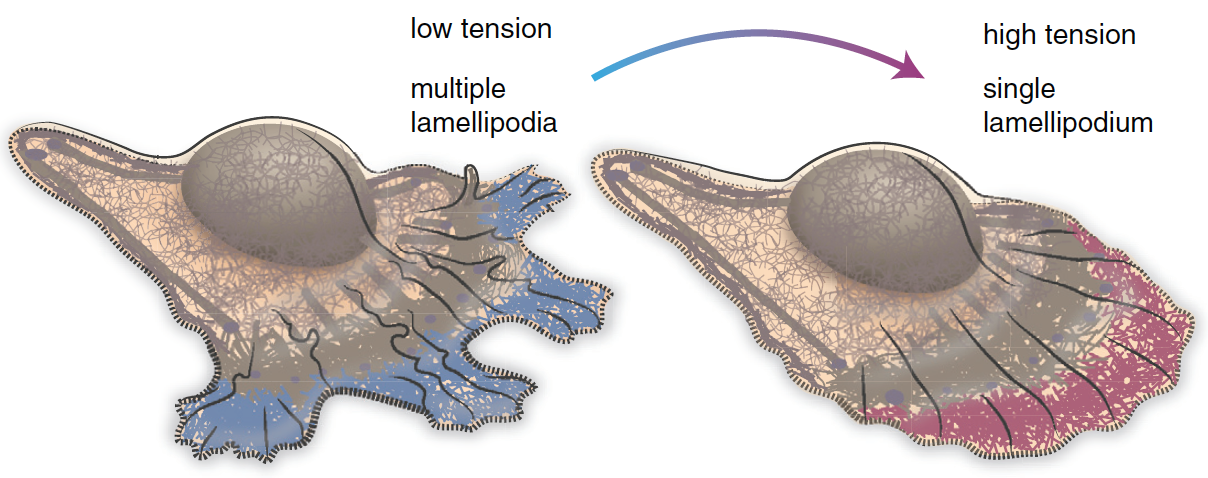
Cell motility involves continuous cycles of protrusion, adhesion, and contraction of the cell membrane10. Actin-polymerization-mediated protrusion of cell membrane called lamellipodia influence the direction of migration. In the region of cell with low membrane tension, multiple lamellipodia that point in different directions coexist (Figure 3, left)11. As a result, cell migration in any particular direction is not favored. Cells can migrate toward a particular direction by increasing the membrane tension at a specific region of the membrane. Increasing the membrane tension will decrease the number of lamellipodia (Figure 3, right)11. Cells tend to migrate in the direction with fewer lamellipodia11.
Membrane Tension and Endocytosis/Exocytosis
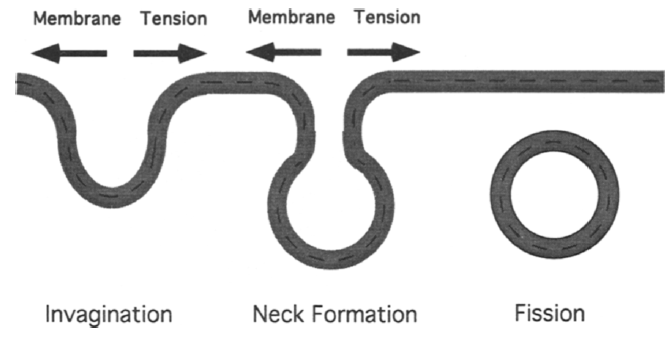
Endocytosis involves formation of cell membrane invaginations, which eventually detach from cell membrane and form vesicles12. Increasing membrane tension or membrane-cytoskeleton adhesion will hinder both invagination and neck formation step (Figure 4)12. Both steps involves membrane deformation.
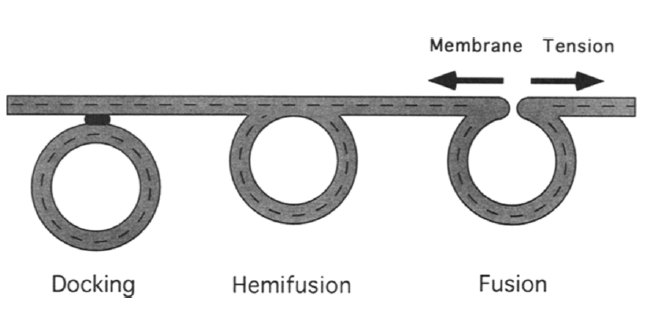
Exocytosis involves vesicles docking to cell membrane and fuse with it12. Unlike endocytosis, increasing membrane tension will favor vesicle and membrane fusion (Figure 5)12. Unlike endocytosis, exocytosis requires minimal membrane deformation.
Membrane Tension and Viral Infections
Polyomaviruses (e. g. Simian virus 40 (SV40), Murine polyomavirus, and BK virus) are nonenveloped DNA viruses13. Capsid protein VP113, a main component of polyomavirus capsid, allows polyomaviruses to overcome membrane tension and infect cells. VP1 binds to glycosphingolipids on cell surface.13 Different types of virus will bind to different types of glycosphingolipids13. For example, VP1 from SV40 binds to GM1 glycosphingolipid13. VP1 binding to GM1 reduces membrane tension by triggering actin cytoskeleton breakdown13. As a result, an invagination of cell membrane is formed, which eventually lead to the endocytosis of the virus13. SV40 endocytosis is shown in Figure 6.
Methods Used to Study Membrane Tension and Line Tension
Methods Used to Measure Surface Tension:
Common methods used to measure membrane tension is shown in Figure 7. One assay for measuring membrane tension is parallel plate confinement assay. In this assay, cells are compressed between two parallel plates. The radii of the principal curvatures of the membrane are measured3. Since the amount of force used to compress the cell is known, you can calculate the membrane tension with the equation shown in Figure 7 (Eq.1)3. Another method of measuring membrane tension is micropipette aspiration. For this method, a small section of the cell membrane is pulled using a micropipette, and the membrane tension is calculated from the cell radius, micropipette tip radius, extracellular pressure, and the suction pressure (Figure 7b, Equation 2)3. Micropipette aspiration can also be used to measure membrane tension from membrane tethers. Since membrane tethers lack continuous cytoskeleton, membrane-cytoskeleton adhesion will have very little (if any) contribution to the membrane tension measured3. Generally, cells are hold in place with a micropipette, and then tethers can be extracted from the cell membrane (Figure 7c, Equation 3)3. Other methods of tether extraction include atomic force microscopy (AFM) and optical tweezers (Figure 7d)3. The cantilever used in AFM can also be used to extract a membrane tether3. To extract membrane tether, optical tweezers can be used to pull on a uncoated polystyrene bead that was attached to the cell membrane14.
Fluorescence resonance energy transfer (FRET) refers to the distance-dependent transfer of energy from one fluorophore to another fluorophore (Figure 8)15. For a more detail explanation of FRET refer to reference 15. Typical FRET experiment involves a pair of flourophores called a FRET pair (a donor fluorophore and an acceptor flourophore). Fluorescence emission spectra of the donor fluorophore must overlap with the fluorescence absorption spectra of the acceptor fluorophore. In practice, only the donor flourophore will be excited. Generally, the florescence intensity ratio of acceptor fluorophore to donor fluorophore is measured. The distance between the donor and acceptor fluorophores affects the FRET efficiency. FRET efficiency increases as the distance between the two fluorophores decreases. Grashoff et al. developed a FRET-base biosensor for membrane tension16. A brief description of the method used in reference 16 is presented here. The biosensor consists of a tension sensor module in-between two halves (Vh and Vt) of vinculin, a membrane-cytoskeletal protein (Figure 9c). The tension sensor module consists of two fluorophores, mTFP1 and venus(A206K), linked together by a spider silk protein flagelliform linker sequence, (GPGGA)8 (Figure 9a). The linker acts as a spring that holds the FRET pair, mTFP1 and venus(A206K), together. Vh and Vt help localized the biosensor to the cell membrane. Once cells are transfected with this biosensor, you can measure the membrane tension by measuring FRET efficiency. As the membrane tension increases, the FRET efficiency decreases because the distance between the two fluorophores increases (Figure 9b). In order to convert FRET efficiency to force, you need to construct a calibration curve (FRET efficiency vs Force). Grashoff et al. attached a similar FRET-base biosensor to a polymer-coated glass surface and a microsphere. They can apply force to the sensor by pulling on the microsphere with an optical tweezer. They then construct the calibration curve by measuring the change in FRET efficiency in response to the amount of force applied to the sensor.
Calculating Line Tension from Domain Nucleation Rate
Blanchette et al. developed a way to calculate line tension from nucleation rate of membrane domain17. A summary of the method used in reference 17 is presented here. First, supported lipid bilayers are heated to 55℃ and then cool down slowly until domain nucleation occurs. Domain nucleation events can be imaged with AFM. Next, lipid bilayers are heated slowly until membrane domains disappear. Averaging the nucleation and melting temperatures will give you the liquidus or miscibility temperature (Ttrans) for liquid-solid and liquid-liquid phase coexistence, respectively18. Then, lipid bilayers are kept 5℃ above phase transition temperature. After the lipid bilayers are homogenized, they are rapidly cool down to various temperatures below Ttrans. During the cooling process, domain nucleation events are imaged with AFM. The line tension (γ) is calculated by fitting the nucleation rate (J) vs 1/TΔT curve with equation 1 for symmetrical domain nucleation, which occurs on both side of the membrane, and equation 2 for asymmetrical domain nucleation, which only occurs on one side of the membrane.
\[ J = A \exp \left( \dfrac{-\pi \gamma^2 a_g T_{trans}}{2k_B \Delta H} \times \dfrac{1}{T \Delta T} \right) \tag{1}\]
\[ J = A \exp \left( \dfrac{-\pi \gamma^2 a_g T_{trans}}{k_B \Delta H} \times \dfrac{1}{T \Delta T} \right) \tag{2}\]
J (obtained with AFM) is number of nuclei that form per unit area per unit time. The molar area of the gel phase, ag, and the enthalpy of the phase transition, ΔH, depend on the lipid composition of the lipid bilayer. T is the temperature, and ΔT is Ttrans – T. A is a pre-exponential factor18.
References
- Kranenburg, M. & Smit, B. Phase Behavior of Model Lipid Bilayers. J. Phys. Chem. B 109, 6553-6563 (2005).
- Sezgin, E., Levental, I., Mayor, S. & Eggeling, C. The mystery of membrane organization: composition, regulation and roles of lipid rafts. Nat. Rev. Mol. Cell. Biol. (2017).
- Diz-Muñoz, A., Fletcher, D.A. & Weiner, O.D. Use the force: membrane tension as an organizer of cell shape and motility. Trends Cell Biol. 23, 47-53 (2013).
- Sheetz, M.P. Cell control by membrane–cytoskeleton adhesion. Nat. Rev. Mol. Cell. Biol. 2, 392-396 (2001).
- Lieber, Arnon D., Yehudai-Resheff, S., Barnhart, Erin L., Theriot, Julie A. & Keren, K. Membrane Tension in Rapidly Moving Cells Is Determined by Cytoskeletal Forces. Curr. Biol. 23, 1409-1417 (2013).
- Salbreux, G., Charras, G. & Paluch, E. Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 22, 536-545.
- Sonnino, S. & Prinetti, A. Membrane Domains and the “Lipid Raft” Concept. Curr. Med. Chem. 20, 4-21 (2013).
- García-Sáez, A.J. & Schwille, P. Stability of lipid domains. FEBS Lett. 584, 1653-1658 (2010).
- García-Sáez, A.J., Chiantia, S. & Schwille, P. Effect of Line Tension on the Lateral Organization of Lipid Membranes. J. Biol. Chem. 282, 33537-33544 (2007).
- Vicente-Manzanares, M., Webb, D.J. & Horwitz, A.R. Cell migration at a glance. J. Cell. Sci. 118, 4917-4919 (2005).
- Pierre, S. & Julie, P. Membrane tension and cytoskeleton organization in cell motility. J. Phys. Condens. Matter 27, 273103 (2015).
- Dai, J. & Sheetz, M.P. Regulation of Endocytosis, Exocytosis, and Shape by Membrane Tension. Cold Spring Harb. Symp. Quant. Biol. 60, 567-571 (1995).
- Ewers, H. & Helenius, A. Lipid-Mediated Endocytosis. Cold Spring Harb. Symp. Quant. Biol. 3(2011).
- Pontes, B., et al. Cell Cytoskeleton and Tether Extraction. Biophys. J. 101, 43-52 (2011).
- Ishikawa-Ankerhold, H.C., Ankerhold, R. & Drummen, G.P.C. Advanced Fluorescence Microscopy Techniques—FRAP, FLIP, FLAP, FRET and FLIM. Molecules 17, 4047 (2012).
- Grashoff, C., et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature 466, 263-266 (2010).
- Blanchette, C.D., Lin, W.-C., Orme, C.A., Ratto, T.V. & Longo, M.L. Using Nucleation Rates to Determine the Interfacial Line Tension of Symmetric and Asymmetric Lipid Bilayer Domains. Langmuir 23, 5875-5877 (2007).
- Blanchette, C.D., Lin, W.-C., Orme, C.A., Ratto, T.V. & Longo, M.L. Domain Nucleation Rates and Interfacial Line Tensions in Supported Bilayers of Ternary Mixtures Containing Galactosylceramide. Biophys. J. 94, 2691-2697 (2008).

