Sample Problems

All of the problems below have had their basic features discussed in an "Analyze This" box in this chapter. This means that the solutions provided here are incomplete, as they will refer back to the analysis performed for information (i.e. the full solution is essentially split between the analysis earlier and details here). If you have not yet spent time working on (not simply reading!) the analysis of these situations, these sample problems will be of little benefit to your studies.

Problem 1.1

The acceleration of a particle moving along the \(x\)-axis is given by the equation:

\[a \left( t \right) = \left(0.300 \frac{m}{s^3}\right)t + \left(2.40 \frac{m}{s^2}\right) \nonumber\]

The particle is at position \(x = +4.60m\) and is moving in the \(-x\) direction at a speed of \(12.0 \dfrac{m}{s}\) at time \(t = 0s\).

1. Find the time at which the particle (briefly) comes to rest.
2. Find the position where the particle (briefly) comes to rest.

Solution

a. From the analysis, we have an equation for the velocity of the particle at all times. Here we are given all the constants we need, namely:

\[\lambda = 0.300 \frac{m}{s^3},\;\;\; a_o = 2.40 \frac{m}{s^2},\;\;\; v_o=-12.0 \frac{m}{s}\nonumber\]

So all we need to do is plug these into the velocity equation, set the velocity equal to zero, and solve for the time in the quadratic equation:

\[v\left(t\right) = 0 = \frac{1}{2}\lambda t^2 + a_o t + v_o \;\;\;\Rightarrow\;\;\; t = \frac{ - a_o \pm \sqrt { a_o^2 - 4 \left( \frac{1}{2} \lambda \right) v_o}}{2 \left( \frac{1}{2} \lambda \right)} = 4.00s\nonumber\]

b. We just computed the time at which it comes to rest, and we already derived the equation for position in the analysis, so we can just plug the values in, noting that the position at time \(t=0\) is given to be \(x_o = +4.60m\):

\[x \left( t=4 \right) = -21.0m \nonumber \]

Problem 1.2

A ball is thrown vertically upward at the same instant that a second ball is dropped from rest directly above it. The two balls are \(12.0m\) apart when they start their motion. Find the maximum speed at which the first ball can be thrown such that it doesn't collide with the second ball before it returns to its starting height. Treat the balls as being very small (i.e. ignore their diameters).

Solution

The balls will collide at the point in time derived in the analysis, with the starting difference in height being given as \(y_o=12.0m\). The problem states that this time must be at least as long as it takes the lower ball to return to its starting point.  In such a flight, the lower ball makes a total displacement of zero, so since we know its acceleration, we can solve for the time of travel in terms of the initial speed:

\[y\left(t\right) = 0 = -\frac{1}{2}gt^2+v_o t\;\;\;\Rightarrow\;\;\; t=\frac{2v_o}{g}\nonumber\]

If we plug this into the equation found in the analysis that relates the starting speed to the time of collision, we will find the starting velocity for which the balls will collide exactly at the lower ball's starting height.:

\[v_o t_{collision} = v_o\left(\frac{2v_o}{g}\right) = y_o\;\;\;\Rightarrow\;\;\; v_o = \sqrt {\frac{g y_o}{2}}=7.67\frac{m}{s}\nonumber\]

Clearly is the lower ball starts at any speed greater than this, then the balls will collide sooner, and they will have not yet fallen to the starting position of the lower ball.

Problem 1.3

A particle moves through space with a velocity vector that varies with time according to:

\[ \overrightarrow v \left( t \right) = \alpha \; \widehat i - \beta t \; \widehat j \;, \nonumber \]

where \(\alpha\) and \(\beta\) are positive constants. Find the rate at which the speed of this particle is changing at time \(t=0\). Does this rate remain the same for all later times?

Solution

We already did all the math we need in the analysis.  The rate of speed change is just \(\dfrac{dv}{dt}\), which is computed in the analysis. Plugging-in \(t=0\) gives a rate of speed change that equals zero!  We see this does not remain true for all values of \(t\), because it only vanishes at \(t=0\).

The reason for this is that the acceleration vector is a constant, and is initially perpendicular to the velocity vector:

\[\overrightarrow v\left(0\right) = \alpha \hat i\;\;\;\;\; \overrightarrow a\left(0\right) = -\beta \hat j\nonumber\]

So at that moment, the acceleration only changes the direction of motion (does not speed it up). But after \(t=0\), the constant acceleration has not changed, and the particle is moving in a new direction, so the acceleration then does change the speed.

Problem 1.4

A bead is threaded onto a circular hoop of wire which lies in a vertical plane. The bead starts at the bottom of the hoop from rest, and is pushed around the hoop such that it speeds up at a steady rate. Find the angle that the bead's acceleration vector makes with the horizontal when it gets back to the bottom of the hoop.

Solution

As stated in the analysis, we can treat the motion tangent to the circle like any other 1-dimensional accelerated motion. In this case, the distance the bead travels is given, so the "no time" kinematics equation (Equation 1.4.3) is most applicable. Let's call the radius of the circle \( R\) and the final velocity \(v\). The tangential acceleration is constant, the bead starts from rest, and the bead travels one circumference, so we get:

\[2a \Delta x = {v_f}^2 - {v_o}^2 \;\;\; \Rightarrow \;\;\; a_\parallel=\dfrac{\left(v^2-0^2\right)}{2\left(2\pi R \right)}=\dfrac{v^2}{4\pi R} \nonumber\]

The centripetal acceleration is toward the center of the circle, so it points upward and its magnitude is simply:

\[a_\bot=\dfrac{v^2}{R} \nonumber\]

The tangent of the angle that the full acceleration vector makes with the horizontal is the vertical component divided by the horizontal component, so:

\[\theta = \tan^{-1} \left(\dfrac{\dfrac{v^2}{R}}{ \dfrac{v^2}{4\pi R}}\right)=\tan^{-1} \left(4\pi \right) = 85^o \nonumber\]

Problem 1.5

A cannonball is fired at an angle \(\theta\) up from the horizontal at a speed of \(v_o\) along level ground. A second cannonball is fired at the same speed, but at a different angle.  Both cannonballs travel the same horizontal distance before landing, but one of the cannonballs takes twice as long to make the journey as the other. Find the two angles at which the cannonballs are launched.

Solution

In the analysis, we found that except for a \(45^o\) launch angle, there are two values that correspond to the same range for a given launch velocity, and that these angles are complementary. From the vertical equation in the analysis, we have the following flight time for a given angle and launch speed:

\[t=\dfrac{2v_o\sin\theta}{g}\nonumber\]

This applies to both cannonballs, so accumulating everything together we get:

\[\left. \begin{array}{l} t_1=\dfrac{2v_o\sin\theta_1}{g} \\ t_2=\dfrac{2v_o\sin\theta_2}{g} \\ \theta_1=90^o-\theta_2\ \\ t_1=2t_2 \end{array}\right\}\;\;\;\Rightarrow\;\;\; \sin\left(90^o-\theta_2\right) = 2\sin\theta_2\;\;\;\Rightarrow\;\;\; \cos\theta_2=2\sin\theta_2\;\;\;\Rightarrow\;\;\; \theta_2=\tan^{-1}0.5=26.6^o,\;\;\theta_1=63.4^o\nonumber\]

Problem 1.6

Two warlords aim identical catapults (i.e. they both release rocks at the same speed) at each other, with both of them being at the same altitude. The warlords have made the necessary computations to crush the other, and fire their catapults simultaneously. Amazingly, the two stones do not collide with each other in mid-air, but instead the stone Alexander fired passes well below the stone that Genghis shot. Genghis is annihilated 8.0s after the catapults are fired, and Alexander only got to celebrate his victory for 4.0s before he too was destroyed.

1. Find the maximum height reached by each of the rocks.
2. Find the amount of time that elapses from the launch to the moment that the rocks pass each other in the air.
3. Find the angles at which each warlord fires his rock.

Solution

Conceptual analysis of this problem is found here.

a. The time it takes a rock to travel to its peak height and back down again is equal to twice the time it takes to travel down from its peak height. Traveling down from its peak height, it starts with zero initial velocity, so we can calculate the height immediately for each rock:

\[ h_{A} = \frac{1}{2}g\left(\frac{t_A}{2}\right)^2 = \frac{1}{2} \left( 9.8 \dfrac{m}{s^2} \right) \left( \frac{8.0s}{2} \right)^2 = 78.4m \\ h_{G} = \frac{1}{2}g\left(\frac{t_G}{2}\right)^2 = \frac{1}{2} \left( 9.8 \dfrac{m}{s^2} \right) \left( \frac{8.0s+4.0s}{2} \right)^2 = 176.4m \nonumber \]

b. The x–components of the velocities of the rocks never change, and since it takes 12s for Genghis’s rock to travel the same horizontal distance as Alexander’s rock traveled in 8s, Alexander’s rock is traveling in the x-direction at a rate 1.5 times as great as Genghis’s rock is traveling in the x–direction. When they are at the same x–position (passing each other), the distance each has traveled is each one’s velocity times the time we are looking for, and we can express both of these distances in terms of the x–component of Genghis’s rock using the ratio described above:

\[ \begin{array}{l} x_A=v_{Ax}t, \;\;\;\;\; v_{Ax}=1.5v_{Gx} \;\;\; \Rightarrow \;\;\; x_A=1.5v_{Gx}t \\ x_G=v_{Gx}t \nonumber \end{array} \]

Since the rocks travel from both ends and are now at the same horizontal position, the sum of the distances they travel equals the total separation of the two warlords. This allows us to calculate the time:

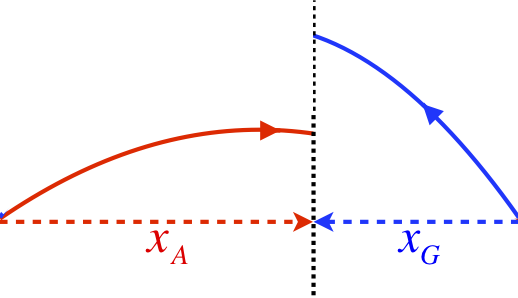
\[ x_A + x_G = x_{tot} = v_G t_{tot} \;\;\; \Rightarrow \;\;\; \left( 1.5v_G \right) t + v_G t = v_G \left( 12.0s \right) \;\;\; \Rightarrow \;\;\; t=\dfrac{12.0s}{2.5} = 4.8s \nonumber \]

c. Clearly there are two different angles that will result in the rock traveling the same distance. One can see this from the range equation, but from a physical standpoint, this happens because one rock spends less time in the air but has a greater x–velocity, while the other spends more time in the air with a smaller x–velocity. To spend 1.5 times as long in the air, Genghis’s rock needs to start with 1.5 times as much vertical component of velocity as Alexander’s rock. This means that the ratios of the x and y components of the two rock velocities are inverses of one another, which means that the two angles are complimentary (i.e. \(\theta_A = 90^o – \theta_G\)). But the total speeds of the rocks are the same, so:

\[\left. \begin{array}{l} v_{Ax} = v_o \cos \theta _A = v_o \cos \left( 90^o - \theta _G \right) = v_o\sin \theta _G \\ v_{Gx} = v_o\cos \theta _G \end{array} \right\}\;\;\; \Rightarrow \;\;\;\dfrac{v_{Ax}}{v_{Gx}} = 1.5 = \dfrac{\sin \theta _G}{\cos \theta _G}\;\;\; \Rightarrow \;\;\;\left\{ \begin{array}{l} \theta _G = \tan ^{ - 1}1.5 = 56.3^o\\ \theta _A = 90^o - \theta _G = 33.7^o \end{array} \right. \nonumber\]

Problem 1.7

You stand on the bank of a river, contemplating swimming across, but the place where you hope to cross is just upstream of a dangerous waterfall. When you look at the speed of the river, you estimate that it is about the same speed as you are able to swim. You realize that you can only swim so far in the cold water at this speed before your muscles shut down, and in still water you estimate that this distance is about \(100m\). The width of the river is about \(80m\).

1. Find the minimum distance that you must start upstream of the waterfall in order to not be swept over it.
2. If the river flows west-to-east and you start on its south shore, compute the direction in which you must swim in order to get safely across if you leave from the starting point computed in part (a).

Solution

The analysis discusses the relevant reference frames in this problem: the river, the swimmer, and the Earth.

a. Clearly to minimize the distance upstream that you need to start, you must swim with a component of your velocity relative to the river being upstream. The more you are able to turn yourself upstream, the less you will float downstream, and the closer you can start to the waterfall. But there is a limit to how far you can swim relative to the water, so your angle with the river must be such that when you reach your limit relative to the river, you reach the other side. The velocities are all constant and the time spans are all equal, so they are proportional to the displacements, which we can draw:

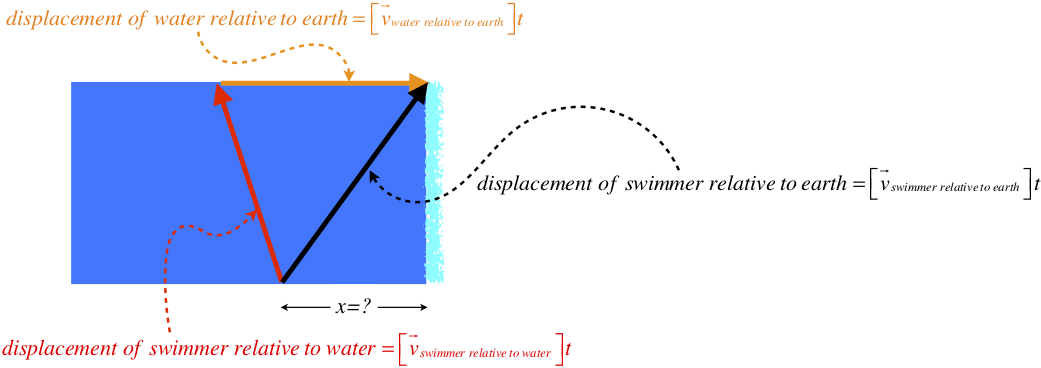
We are given that the speed of the river relative to the earth is the same as the speed of the swimmer relative to the water, so we’ll call that quantity \(v\), and the width of the river (which we know), we’ll call w. From the Pythagorean theorem we can get the distance swum upstream against the current:

\[distance \; swum \; against \; water = \sqrt{\left(vt \right)^2 - \left(w \right)^2} \nonumber \]

The distance the water moves downstream relative to the earth is clearly vt, so the total distance the swimmer moves downstream is:

\[x = vt - \sqrt{\left(vt \right)^2 - \left(w \right)^2} \nonumber \]

But we actually know the value of \(vt\), because it is the maximum distance that the swimmer can go in the water. Plugging in all the values therefore gives our answer:

\[x = \left(100m \right) - \sqrt{\left(100m \right)^2 - \left(80m \right)^2} = 40m \nonumber \]

b. The angle is easy to determine, since we know the length of the displacement vector of the swimmer relative to the water and the width of the river:

\[\cos\theta = \dfrac{w}{vt} = \dfrac{80m}{100m} \;\;\; \Rightarrow \;\;\; \theta = 37^o west \; of \; north \nonumber \]