2.1: Forces, Fundamental and Composite

Newton's First Law

We now understand how to handle motion in all its forms, but really we haven’t done much in the way of physics, because we haven’t explained what causes these different motions. In ancient times, Aristotle made the observation that eventually all things seem to come to rest, which led him to conclude that a stationary condition was “natural” for everything (well, everything on Earth – heavenly bodies never seemed to stop moving). He stated that keeping things moving requires constant pushing or pulling, or it would eventually settle into a state of rest.

This is a very intuitive way of describing the nature of things, and most people even today see the world this way. It wasn’t until nearly 2000 years after Aristotle that a genius born on Christmas day would overturn that long-held belief. His name was Isaac Newton, and he claimed that in fact nature behaved in precisely the opposite manner. Newton claimed that it was not natural for objects to be at rest unless they were already at rest. If they were already moving, then it was natural for them to continue moving. He claimed that it was the fact that objects on Earth could not escape the slowing effects of pushes and pulls that accounted for them always coming to rest.

But Newton was more specific about this “natural state of motion.” He stated that the only type of motion that would continue indefinitely if undisturbed by pushes or pulls was constant velocity (speed and direction) motion. That is, any motion that involved changes of speed or direction requires a push or pull.

Newton's 1st Law of Motion

Objects at rest or in motion at a constant speed in a straight line will remain in that state unless acted upon by an external influence.

Conceptual Question

A stone is swung in a horizontal circle while tied to a string, which suddenly breaks.  Which of the paths below represents the motion the rock will follow? (these are paths viewed from above)

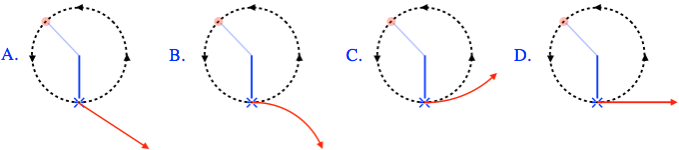
5. It depends upon whether the rock is speeding up or slowing down at the moment the string broke.

Solution

(d) The rock starts off moving in a circle, which means it was accelerating and according to the first law, it must have had a force on it.  From the description of the motion, the only force contributing to that net force had to be the tension force by the string.  At the instant that the string breaks, the force vanishes, which means that the rock can no longer accelerate.  Zero acceleration means constant velocity, which means that whatever speed and direction the rock had at the moment that the string broke, it must maintain.  Note that the rock has no memory whatsoever of the fact that it was accelerating just a moment before, so it neither continues accelerating for a short time, nor does it compensate for the previous acceleration by accelerating the other way.

Definition of Force

What we have been calling “pushes and pulls” or “external influences” is called force in physics. Most people have an intuitive idea of what force is, and like so many other physics concepts, this intuition is very likely wrong. We'll start by saying what force is not, then move on to its definition.

Alert

Force is not a quantity stored in, or possessed by, an object. Force cannot be transferred from one object to another, nor can one claim that one object “has” more force than another. This can be a hard notion to shake.

Definition: Force

Force is an interaction between two objects, which comes in the form of a push or a pull.

This simple definition belies some very difficult conceptual ideas that people (like Aristotle, and indeed every human since) struggle with, as we will soon see. The trick will be for us to develop some tools we can rely on that will help us get past our misconceptions. We will develop these tools in the sections to come, but here we will focus on the nature of forces that we encounter in everyday life. But one thing we can conclude from this is that pushes and pulls have definite directions, which means that we can conclude that forces are vectors.

Individual Particles vs. Systems of Particles

When we consider forces on and/or by individual particles, we find a couple of things.  First, all such forces act "at a distance."  That is, particles never actually touch each other – it is useful to think of particles as being merely points, with no extension in space, which makes them touching each other rather problematic. So these particles are somehow aware of each other's presence, and exert pushes and/or pulls on one another. The second thing we find is that these forces only come in a limited variety of just 4 types: gravitation, electromagnetic, and two different types of nuclear forces. It is believed that while these forces all manifest very differently (the forces depend upon different particle properties, and vary differently with particle separation), they ultimately are different manifestations of a single force. Indeed, it was once thought that the electric and magnetic forces were distinct, until it was shown quite conclusively that they are two sides of the same coin, and they are now referred to as a single force. It also happens that modern theorists have shown that one of the nuclear forces (called the "weak nuclear force") is just a different manifestation of the electromagnetic force. This combination is therefore often referred to as the "electroweak" force amongs physicists. This particular unification of seemingly disparate forces is much harder to describe to those not fluent in the languages of high-energy physics and advanced mathematics, and so the simpler (older) claim that there are four such forces lingers.  These four (three) action-at-a-distance-between-individual-particles forces are called the fundamental forces.

Suppose now that we have two collections of particles, each of which we categorize as a "system", or more crudely, as an "object." These two objects exert forces on one another in the following way: Every particle in system #1 exerts a fundamental force on every particle in system #2.  The sum of all these forces we can now call a single "force between the two objects." Clearly due to its cumulative nature, it is not "fundamental," but it is still nevertheless a force (we will use the word composite to describe these non-fundamental forces), in that it will cause the affected objects to no longer remain at rest or in motion in a straight line at constant speed. Given that much of what we will discuss are macroscopic systems where objects comprised of trillions of trillions of particles exert forces on each other, it makes sense to categorize some of the more common examples of these composite forces. But under it all, it is important to remember that all of these flavors of forces are just macroscopic special cases of just a few fundamental forces.

Digression: Quantum Mechanics vs. Classical Mechanics

All of the discussion here (and later in this textbook) about fundamental forces and individual particles assumes that we are employing a "classical" mechanical model for describing the universe. We have known for a long time that the realm of the very small (i.e. individual particles) does not actually function in this manner. Nevertheless, physics is about using whatever model we like that describes nature in a consistent manner that has predictive value for the conditions imposed on it. This classical model will not work if we take an extremely close look at what is happening to particles, but here we are only using this model to get a more general sense for what is happening macroscopically – the world where we look at enormous systems of particles ("objects" like chairs and bicycles) – and for this purpose, this model serves us very well.

Van der Waals Force

There is clearly a wide chasm that must be bridged in order to move a discussion from a fundamental force between two point-like particles to a force between two cars in a traffic accident. The most important step in this daunting journey boils down to a simple observation of what happens when two small clusters (systems you can call molecules, if you prefer) of particles are brought into proximity with each other...

• When they are at just the right separation, the clusters do not exert a net force on each other. Every one of the individual particles of one cluster exerts a fundamental force on every particle in the other cluster, but the sum total of these forces is zero.
• When the clusters are moved closer together than the "perfect separation" described in the previous bullet, a strange thing happens – the sum total of fundamental forces between individual particles no longer comes to zero.  When they get too close, the clusters repel each other.
• If the clusters are pulled slightly farther apart than the "perfect separation", then the composite force between the clusters becomes attractive.

This simple-yet-amazing property of this composite force (typically referred to as a Van der Waals force) resulting from many electromagnetic forces is what we have to thank for our very existence. If systems of particles could only (as in the case of individual particles) only exert either attractive or repulsive forces on each other, then all matter would either collapse in on itself or explode. We will not study the mathematics of this type of composite force for several chapters, but we will refer back to its characteristic properties frequently later as we describe even more crude composite forces that we will work with in the macroscopic world.

Alert

An astute reader that looks up "Van der Waals forces" (or who perhaps studied them already in a chemistry class) will undoubtedly find that this name is generally given specifically to forces between particles in a gas. Indeed, this is the specific phenomenon that Van der Waals studied. But it turns out that the property is much more robust than only applying to gases, so we are taking some license here and referring to all forces that behave similarly with this moniker. In a later chapter, we will discuss a mathematical model for this kind of force called the "Lennard-Jones potential." The point is that we should not get too worked-up about labels we give this physical behavior – it is the behavior itself that is important.