2.2: Macroscopic Forces

Macroscopic Composite Forces

As instructive as it is to discuss the microscopic underpinnings of forces, at some point we need to have some working knowledge of the macroscopic forces we will be dealing with in everyday mechanics problems. We undertake here to make an accounting of these very forces.

gravity

As mentioned in the previous section, most of our macroscopic composite forces will ultimately stem from Van der Waals forces, which themselves are a composite of just the electromagnetic force. But there is one exception – gravity. "But wait," you say, "isn't gravity a fundamental force?" Yes, when it is between two particles. But the Earth is comprised of many particles, and so is a hammer, so when a hammer is pulled downward by the Earth, the force is composite. If we were to look very closely at the details of the force between these two objects, we would find that we have to describe it somewhat differently from the fundamental force case.

Alert

In an attempt to maintain the distinction, we will refer to the fundamental force between particles (which we will study in Chapter 7) as "gravitation", and the composite force between objects (one of them almost always being the Earth) as "gravity."

What makes gravity so different as a macroscopic force from the others we will discuss here is that it doesn't display a Van der Waals sort of attract-if-pulled-apart-repel-if-pushed-together behavior between clusters.  Unlike electromagnetism, there is no repulsive element of gravity, so each of the individual particles in one cluster only attracts the individual particles in the other cluster, resulting in only attractive forces between clusters.

Gravitation, like all fundamental forces, depends upon two things – a property of the gravitating particles (namely, their masses), and the separation of those particles. When we are talking about the composite gravity force on a stone at the Earth's surface, we assume that the stone never gets particularly far from that surface (even a mile above the Earth's surface is only about 1/4000th the radius of the Earth), so under the assumption that the stone never gets really far from the Earth (like outside its atmosphere), the gravity force remains only a function of the mass of the Earth, \(M_E\), and the radius of the Earth, \(R_E\), (both are fixed numbers), and the mass of the stone, \(m\), (which can be different for different stones). This all boils down to a simple mathematical description of the gravity force on objects like stones: It acts downward – toward the Earth, because it is only attractive – and is proportional to the mass of the object.  The constant of proportionality we will call "\(g\)", a symbol we have not coincidentally already used to represent the acceleration of a freely-falling object. It is this constant that depends on the mass and the radius of the Earth, \(g=GM_E/R^2_E\), where \(G\) is the gravitational constant. We'll return to this when we cover gravitation in a later section. But for now:

\[\overrightarrow F_{gravity} = mg\left(-\hat j\right)\;,\;\;\;\;\;g=9.8\frac{m}{s^2}\]

The direction of this force (downward, toward the Earth) is expressed in the unit vector direction, \(-\hat j\).

elastic (spring) force

A good starting point for macroscopic manifestation of the Van der Waals effect is the force exerted by a spring, often referred to more generically as an elastic force. This is a macroscopic force that very closely mimics the behavior of Van der Waals forces, in that compressing the spring between two objects (moving them closer together) results in a force from the spring that seeks to push the objects apart, and stretching the spring results in a force that seeks to pull them together. There is also an "equilibrium" length of the spring at which no force is exerted at all. All forces of this nature are given the generic description of restoring forces, in that the force induced by making a change from equilibrium seeks to restore the equilibrium.

The similarity between the spring force and Van der Waals forces is so strong that physicists frequently use particles attached springs as a model for microscopic behavior. Naturally there are not any tiny little springs bonding molecules to each other, but the model allows for workable mathematics that yields remarkably accurate predictions.  The simplified mathematics is apparent in the formula that accompanies the elastic force. The elastic force depends upon three things:

• the displacement from the equilibrium (the distance that the spring is stretched or compressed)
• the "stiffness" of the spring (usually referred to as the spring constant)
• whether the spring is compressed or stretched (this only affects the direction of the force, while the two previous items affect the magnitude)

Figure 2.1.1 – Elastic Restoring Force

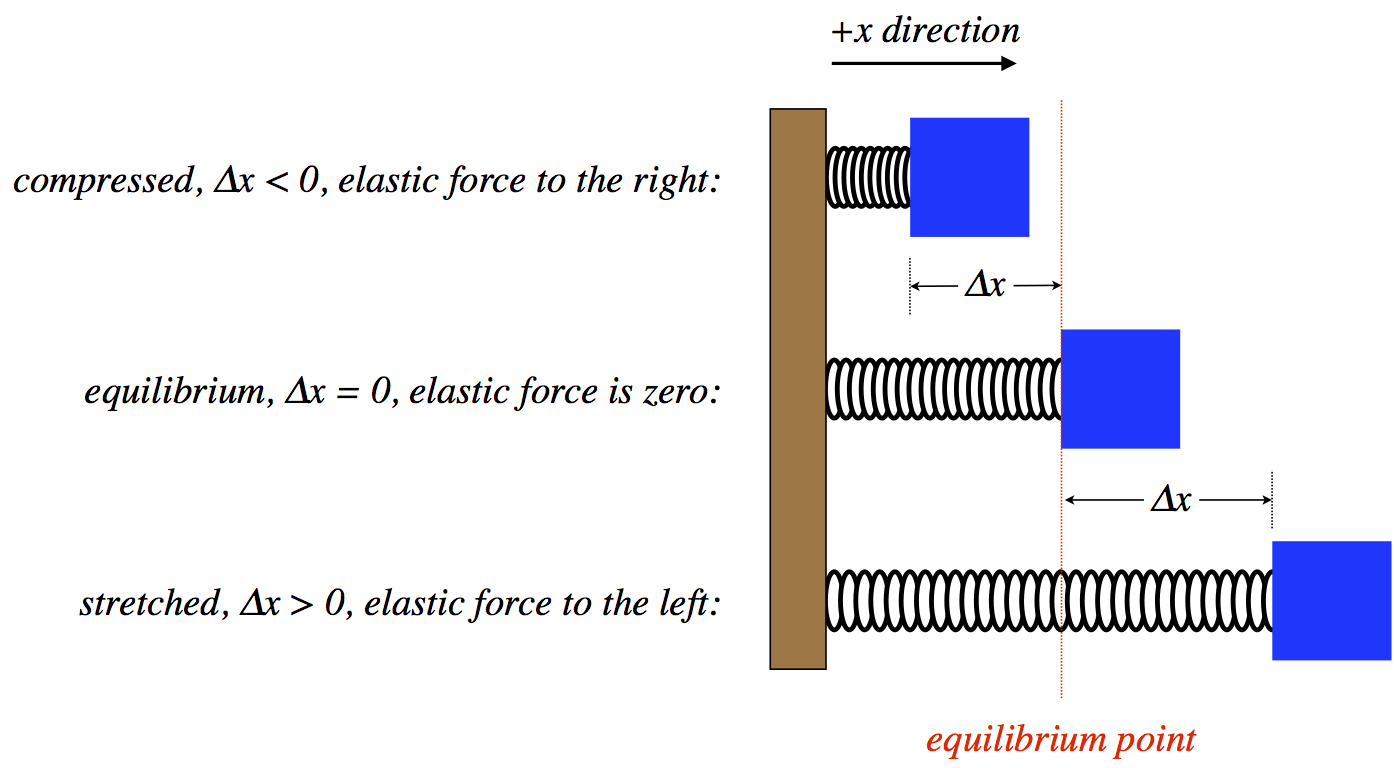
Putting these properties together mathematically gives:

\[\overrightarrow F = k\left(-\overrightarrow{\Delta x}\right) \]

The value \(k\) is the spring constant (which is always a positive number, and measures how stiff the spring is), \(\overrightarrow{\Delta x}\) is the displacement vector of the object on the spring from the equilibrium point, and the minus sign indicates the restoring nature of the force, as it always points in the opposite direction of the displacement. This formula is commonly known as Hooke's Law, named after a contemporary (and rival) of Newton's.

Alert

Note that the usage of the "\(\Delta\)" in Hooke's law is different from how we have used it up to this point – here it refers to a difference in locations, rather than a change that occurs over a period of time.

tension

Suppose that a spring is attached to a fixed point (say a wall), and someone pulls on the other end with a certain amount of force.  Naturally the spring will stretch until the Hooke's law force grows to the point where it balances the pulling force. At this point, the stretched spring also exerts the same Hooke's law force on the wall. In other words, the force the person exerts on the spring is "transmitted" all the way to the wall. If we don't care about the intermediate elements of this force (i.e. the amount the spring stretches), or equivalently, if the spring constant is so large that the stretch is negligible, then we have a simplified version of the elastic force called tension, which we will usually denote with the symbol "\(T\)".

There is no "formula" for tension, as we saw for gravity and springs, because it is really just a reactionary force – it is determined by other applied forces that are present. The amount that the person pulls on the string attached to the wall is the amount that the tension force pulls on the wall. This cannot be expressed as a formula involving quantities related to the string and wall.

An interesting element of tension has to do with how its transmission direction can be redirected. For example, one can pull on a rope attached to an object without the direction of the applied pull being the same as the pull on the object, if a pulley is involved. We will spend some time on the effects of pulleys in the sections to come.

Alert

One will often see the phrase "tension in the string" used in the context of physics problems. It is very important that one does not conceptually interpret this as force being stored within the string. A more accurate phrase in such cases would be "tension force exerted on the object by the string."

contact (normal) force

In the same way that tension is a simplified version of the elastic force in the case where a spring is stretched, contact force is a simplified version of the elastic force when the spring is compressed. The one major difference is that there is no intermediate object like a rope – it occurs when two objects are in direct contact with each other. Of course, what we call "contact" at the macroscopic level is really nothing of the kind microscopically. The clusters of particles at/near the outer surfaces of the two objects that are close to each other repel, thanks to Vans der Waals repulsion. This repulsion is a restoring force similar to that of a compressed spring. But like tension, for this force, we are not concerned with the details of the amount of compression or the stiffness of the springs, just that the compression ceases when the applied force is balanced by the elastic force. Like the tension force, this one is purely reactionary, and therefore has no formula that expresses it in terms of properties of the two objects in contact.

An important property of this force is its direction. In the case of tension the direction was easy – just look at which way the rope is pointing. For the contact force, the direction is always perpendicular ("normal") to the surfaces in contact. Note that the surfaces do not need to be flat – even a curved surface has a well-defined perpendicular at a given point. This property is the source for a perhaps more-commonly used name for this force, normal force, as well as for the most common symbol used to represent it, "\(N\)". 

friction

Another reason that the contact force between surfaces is referred to a normal force is that there is another force that results from two surfaces coming in contact. While the normal force is perpendicular to the surfaces, the friction force is the force between the surfaces that is parallel to those surfaces. As with the normal force, friction is a result of Van der Waals forces between clusters of particles on one object's surface and clusters of particles on the other object's surface. But a critical feature for friction is the microscopic irregularities that exist in the surfaces.

Figure 2.1.2a – Irregular Surfaces Pushed Together

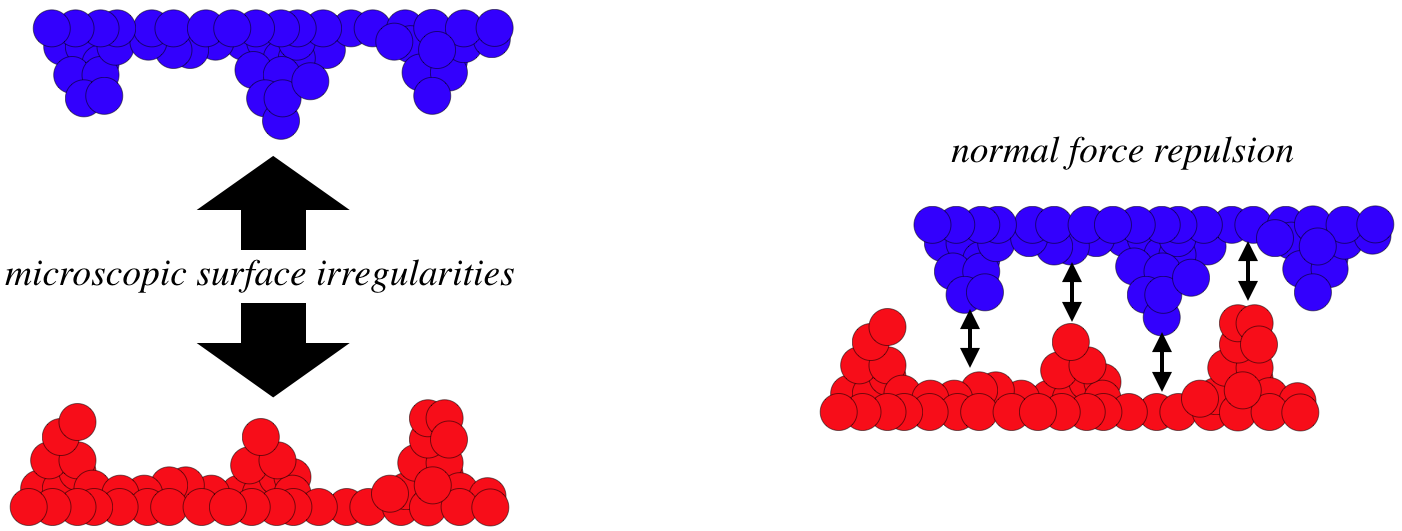
As the surfaces are pushed together and the repulsive normal force starts to take effect, the irregularities naturally "mesh" with each other. This meshing causes attractive and repulsive forces to take effect between the peaks of the irregularities along the direction parallel to the surfaces (horizontally, in the diagram above). If no external force is applied to the surfaces, then these forces between peaks will balance themselves out (the objects will move very slightly across each other) to leave only the normal force between the surfaces. If, however, the surfaces are offset from this equilibrium, some of the peaks will get closer (resulting in a repulsive Van der Waals force), and some will get farther apart (resulting in an attractive Van der Waals force), and the net result is a force that opposes this displacement.

Figure 2.1.2b – Effect of Trying to Slide Surfaces Across Each Other

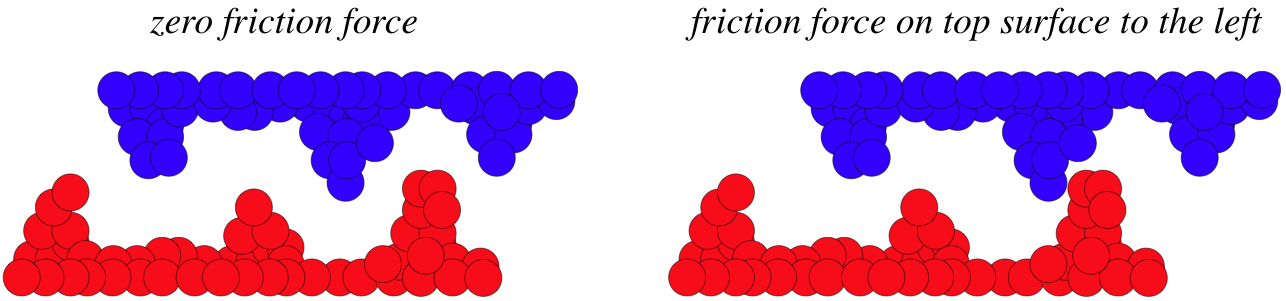
Considering this is a microscopic view of the surfaces, it is clear that they are not shifted very far for this friction force to take hold. Indeed, we would never even notice such a shift. Very much like the case of tension, where we do not observe a stretch of a string, or normal force, where we do not notice the compression of a surface, this friction force is purely reactionary – it appears when we try to slide two surfaces across each other. So this friction force is what is occurring when we try to slide a heavy box across a floor, and it won't move. The friction force comes from the restoring Van der Waals force from trillions of irregularities being displaced, and it exactly balances the applied force. Because it is not related to ongoing sliding of the surfaces across each other, this is called static friction.

Of course, we know that friction also occurs when the surfaces actually do slide across each other as well. The mechanism is essentially the same, just repeated over and over as bumps in one surface encounter new bumps in the other. While static friction opposed the attempted slide of the surfaces across each other, kinetic friction opposes the actual, ongoing, slide. Notice that when a surface is pushed too weakly across another to get them sliding, static friction is in effect, but as soon as that external push exceeds the ability of the static friction force to compensate, the sliding begins and kinetic friction takes over. This moment of sudden loss of the purely-reactionary static friction force is analogous to the tension force suddenly going away when the string breaks.

While the microscopic mechanism for the two types of friction are essentially the same, they do have some differences. For example, it is relevant to ask how the maximum static friction force compares to the kinetic friction force, for two surfaces under the same conditions. To answer this we consider the effect of the "depth" of meshing of the surface irregularities. If the surfaces are pushed closer together, then there are more particle clusters available to engage with each other (it's not just the tips of the peaks anymore), which should make either friction force stronger. If all else is equal, then two irregular surfaces sliding across each other is sort of "bouncing along," and the average depth of the meshing is a little less than if the surfaces are unmoving. We would therefore expect the maximum static friction force for two surfaces at rest with respect to each other to be slightly greater than the kinetic friction force when the surfaces are sliding.

So how can we express all this mathematically? First, we have already determined that the static friction force is reactionary, so there is no equation to express it. However, we also know that the magnitude of this force is limited for any given circumstance – pushing the two surfaces hard enough will get them to slide. So we can express static friction as an inequality:

\[f_{static}\le f_{max}\]

Here \(f_{max}\) represents the maximum force that can exist between the surface irregularities parallel to the surfaces before they start sliding across each other. There are two factors that determine this maximum: how rough the surfaces are (how deep the pits in it go), and how far the surfaces are "meshed." The only reason they don't mesh fully is the repulsive Van der Waals forces that act perpendicularly – the normal force. When the surfaces are pushed harder against each other, increasing the normal force, they mesh more deeply, and the maximum static friction force rises. Experimentation shows that, to a good approximation, the maximum static friction force is actually proportional to that normal force, giving us:

\[f_{static}\le \mu_s N\]

where \(\mu_s\) is a dimensionless constant (usually less than 1) called the coefficient of static friction.

Once the surfaces are actually sliding across each other, the friction force is a fixed value (not less than or equal to some maximum). Once again, this fixed value experimentally is found to be approximately proportional to the normal force, giving us an equality that looks similar to the inequality above:

\[f_{kinetic} = \mu_k N\]

where \(\mu_k\) is called the coefficient of kinetic friction.

Both coefficients of friction reflect properties of the surfaces. It is an oversimplification to say that they give a measure of how deep the jagged irregularities are, but this is not a terrible mental picture to have when thinking about these constants. It should also be noted that most physics problems that involve friction have wording that goes something like, "an object slides along a surface with coefficient of kinetic friction equal to...", but it is important to remember that the coefficient of friction for a single surface makes no sense – it can only really be defined in terms of both surfaces.

It is natural at this point to ask the following question: "How can the magnitude of the kinetic friction force (or the maximum static friction force) depend only upon the normal force and "roughness"? If all else is equal, wouldn't the surface area in contact also play a role?  After all, more surface area means that more surface irregularities encounter each other. But more surface area also means there are more molecules repelling each other perpendicular to the surfaces. So suppose we increase the surface area without changing the normal force. To get the same normal force from more repulsing molecules, those molecules need to be farther apart, which means that the surfaces don't "mesh" as deeply. Less meshing means less friction force.  So it turns out that the increase in the number of irregularity "encounters" that comes with more surface area is accompanied by less depth in meshing, and these two effects cancel each other out, making contact surface area (to a good approximation) an unimportant factor in calculating friction force.

drag

The final macroscopic force to add to our pantheon is called drag. This comes about whenever an object is moving through a fluid. If the fluid happens to be air, then this force is commonly referred to as air resistance. Drag is similar to kinetic friction in that its direction on a moving object is always opposite to that object's motion relative to the dragging fluid. It differs from kinetic friction in that the magnitude of the drag force varies with the speed of the object relative to the fluid, whereas kinetic friction remains approximately constant for all speed.

Microscopically, the drag force can be viewed as countless collisions of the moving object with the tiny particles in the fluid. Again, the particles in the moving object don't actually touch the fluid particles, but as the object moves through the fluid, the particles get close enough together to repel, and naturally that repulsion acting on the object is in the opposite direction to its motion through the gas.

The mathematics of drag turns out to be quite complicated, though three of the physical properties that factor in are fairly easy to enumerate:

• relative speed of the object and the fluid – By increasing the speed, there are more collisions with fluid particles per second, which increases the associated force.
• cross-sectional area of the object through the fluid – The number of particles that strike the object increases as the cross-sectional area (the area perpendicular to the direction of motion) is increased.
• density of the fluid – This is a measure of how close together the particles in the fluid are to each other. Increasing the density therefore increases the number of particles in the fixed space through which the object passes, and more particles means more collisions, which results in more force.

Interestingly, the shape of the object also has an effect, because the fluid flow around the object will also result in forces.  That is, two objects can have the same cross-sectional area, but one can be more aerodynamic (for gases) or hydrodynamic (for liquids) than the other, and this plays a role in the amount of drag force.

Putting all this together, we get a not-quite-fully-formed formula that looks like:

\[F_{drag}= (constant)\rho A f\left(v\right)\]

where \(\rho\) is the fluid density (measured in mass per volume), \(A\) is the cross-sectional area of the object, and \(f\left(v\right)\) is some unknown function of the speed of the object relative to the fluid that gets larger as \(v\) gets larger. This somewhat unsatisfying result is usually packaged in the following way: Choose a function of \(v\) that comes close for "typical" speeds, and then lump together all the other factors (two of which are the appropriate tweak to the velocity function and the shape of the object, but there are a few more) into what is called the drag coefficient, \(c_d\) (which is then determined experimentally), to give:

\[F_{drag}= \frac{1}{2}c_d\rho v^2 A\]

Apart from a couple very basic applications (such as something called "terminal velocity", which we will discuss later), we will not typically complicate our physics discussions by incorporating the effects of drag. Phrases like "ignoring air resistance" will be quite commonplace going forward, to the point where they will be understood to be in effect unless explicitly stated otherwise.