3.6: Mechanical Advantage and Power

Reconciling Work with Mechanical Advantage

Back when we first talked about pulleys, we said that the block-and-tackle device was useful for lifting heavy objects.  The figure below shows two blocks lifted the same distance by pulling on a rope in a pulley system. We know that it requires less force to lift the same mass for the case on the left than the case on the right, but now let's compare the amount of work done by the pull force in the two cases. In both cases, the block is raised the same distance, and in both cases it starts and ends at rest.

Figure 3.6.1 – Work Done with Pulley Systems

The pull force acts downward on the end off the rope, and the direction the end of the rope moves is downward, so there is positive work done in both cases. With identical blocks, the force required to be applied to the rope for the left case is half as great as the force required to lift the block in the right case. However, in order to lift the block the same distance from where it started, the rope must be pulled twice as far in the right case than in the left case, thanks to the pulley ratio constraint. With half the force acting over twice the distance, the amount of work done is the same. The multiplicative factor by which the force needed for the load exceeds the force exerted on the system is called mechanical advantage (MA):

\[MA \equiv \dfrac{force~on~load}{force~applied}\]

What we have found is that since the work done on the load is the same as the work done from outside, the mechanical advantage can also be expressed in terms of the ratio of the displacement of the object on which the applied force acts (e.g. the end of the rope in a block-and-tackle), and the displacement of the load:

\[W_{in}=W_{out}~~~\Rightarrow~~~F_{applied}\Delta x_{applied}=F_{on~load}\Delta x_{load}~~~\Rightarrow~~~MA=\dfrac{\Delta x_{applied}}{\Delta x_{load}}\]

The mechanical advantage can of course be multiplied by including more pulleys (or mor loops around the same pulley) – the pulley constraint ratio discussed earlier is the same as the mechanical advantage in every case.

So it appears that the block & tackle (and simple machines more generally) trade effort (force) for displacement, such that the amount of work done remains the same. Let's see if we see a similar result for the case of the inclined plane.

Figure 3.6.2 – Work Done with an Inclined Plane

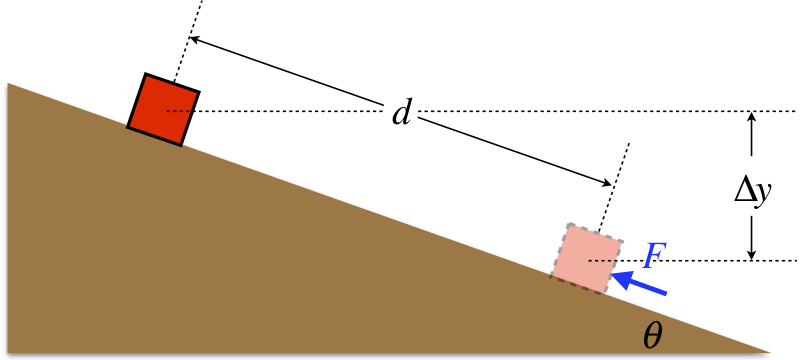
Let's assume that the inclined plane shown in the figure above is frictionless, that the force applied to the block is parallel to the plane, and that it is just enough so that the block moves at a constant speed up the plane. A FBD (without the irrelevant normal force which acts perpendicular to the motion) looks like:

Figure 3.6.3 – Partial FBD of Block on Plane

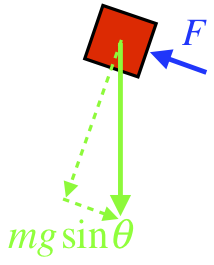
For the block to stay at a constant speed, the force up the plane must equal the force down the plane, which means:

\[ F = mg \sin \theta \]

So the force required is reduced by the factor \(\sin \theta \) compared to lifting the block straight up. But from trigonometry, the distance the block must be pushed is:

\[ d = \frac{\Delta y}{ \sin \theta } \]

When we multiply the force by the distance to get the work done, we get:

\[ W = Fd = \left( mg \sin \theta \right)\left( \frac{\Delta y}{ \sin \theta } \right) = mg \Delta y \]

This is the amount of work required to lift the block straight up at a constant speed, so once again the simple machine trades extra distance for less force to get the same work. This agrees with the result we have already obtained, using gravitational potential energy. [Note: The change in gravitational potential energy equals the negative of the work done by the gravity force. In this case, we have computed the work done by us, and since the force we apply to do the work is in the opposite direction as the gravity component, we get a positive value.]

Power

We take a moment now to introduce yet another physics word whose common usage in English is very different from its meaning in physics.

Definition: Power

Power is the rate at which work is performed.

Note that just like we can talk about the work done by an individual force or a collection of forces, we can also talk about the power "delivered" to a system by one or more forces. For example, if a car is moving at a constant speed on level ground, its kinetic energy is not changing over time, so no total work is being done on it. If no work is done on it over time, there is no net power being delivered to it. But clearly the engine of the car is doing something. So it is useful to break up the power delivered by separate sources if we want to isolate the rate at which the engine is doing work, without worrying about the rate at which air resistance and friction are are doing negative work on the car to bring the total to zero.

Mathematically, we therefore have for the power delivered by a given force is:

\[ P \equiv \dfrac{dW}{dt} \]

Since the units of work is Joules, the units of power is Joules per second, which we rename as: watts (\(W\)).

One nice shortcut for power involves the force doing the work and the velocity of the object on which the work is being performed:

\[ dW = \overrightarrow F \cdot \overrightarrow{dl} \;\;\; \Rightarrow \;\;\; P = \dfrac{dW}{dt} = \dfrac{\overrightarrow F \cdot \overrightarrow{dl}}{dt} = \overrightarrow F \cdot \dfrac{\overrightarrow {dl}}{dt} = \overrightarrow F \cdot \overrightarrow v \]

Note that this is the power delivered to the moving object (i.e. the rate at which energy is added to or taken away from the object) at the instant that the force and velocity are the vectors given above. If this is integrated from a starting time to a final time, the result is the total work done over that time span by the force.

Exercise

Two forces act on a moving object of mass \(1.50kg\), causing its velocity to change over time. One of the two forces is given below, as is the velocity as a function of time.

\[\vec F_1 = \left(3.00N\right)\;\hat i + \left(4.00N\right)\;\hat j\;\;\;\;\;\;\vec v\left(t\right)=\left(0.800\frac{m}{s^2}t-4.0\frac{m}{s}\right)\;\hat i+\left(1.8\frac{m}{s}\right)\;\hat j\nonumber\]

 At one moment in time, only the force not given above is delivering power to the object. Find the amount of power delivered by this force at this moment in time.

Solution

First we need to find the time at which this is occurring. We know that the force given above is not delivering any power at this moment, so its dot product with the velocity vector must vanish, giving:

\[0=\vec F\cdot\vec v = \left(3.00N\right)\left(0.800\frac{m}{s^2}t-4.0\frac{m}{s}\right)+\left(4.00N\right)\left(1.8\frac{m}{s}\right) \;\;\;\Rightarrow\;\;\; t=2.00s \nonumber\]

We can find the net force on the particle as a function of time by computing the acceleration from the velocity and using Newton's 2nd Law:

\[\vec F_{net}=m\frac{d\vec v}{dt}=\left(1.50kg\right)\left(0.800\frac{m}{s^2}\right)\hat i = \left(1.20N\right)\hat i\nonumber\]

This results in a total power delivered to the object as a function of time that is:

\[P_{tot}=\vec F_{net}\cdot\vec v=\left(1.20N\right)\left(0.800\frac{m}{s^2}t-4.0\frac{m}{s}\right)\nonumber\]

At the time computed above, the force \(\vec F_1\) is not delivering any power, so all of the total power must be coming from the second force. Thus:

\[\text{at }t=2.00s:\;\;\;\; P_2=P_{tot} = -2.88W\nonumber\]

Analyze This

A particle starts from rest and experiences a net force that has a constant magnitude. This force does change direction, however, such that the particle is made to move in a circular path.

Analysis

To get the particle moving, the force must be tangential to the circle around which the particle will eventually be traveling. But as the particle speeds up, in order to continue its motion in a circle, the component of the net force toward the center of the circle grows, and since the magnitude of the force remains fixed, there is a decreasing amount of tangential component of the force that goes into speeding up the motion of the particle.

For a given mass of particle and radius of circle, there is a limited speed at which the particle can travel – the speed at which the entire force acts to maintain the centripetal acceleration:

\[F=m\frac{v_{max}^2}{R}\;\;\;\Rightarrow\;\;\;v_{max}=\sqrt{\frac{FR}{m}}\nonumber\]