4.1: Repackaging Newton's Second Law
- Page ID
- 62997
Definition of Impulse
In chapter 2, we made a point of emphasizing that force is not possessed by objects – it is an interaction between them. One way we know this is that if the same force is exerted on identical objects that start at rest, the two objects are not necessarily moving the same afterward. There is an important ingredient missing here – the duration that the force acts. Since the force causes an acceleration, the longer it acts, the more the velocity is affected. So multiplying the force by the amount of time it acts may provide us with a useful quantity. The force may be changing magnitude or direction while it acts, but over a very short time this product is:
\[d\overrightarrow J = \overrightarrow F dt \]
If we want to know the totality of this quantity over a finite time interval, we need to add up all these little contributions. We give this quantity the name impulse.
Definition: Impulse
\[\overrightarrow J_{tot}\left(t_A \rightarrow t_B\right) \equiv \int \limits_{t_A}^{t_B} \overrightarrow F_{net} dt \nonumber \]
This quantity is the sum of the product of the forces and the times over which those forces act. This certainly sounds very similar to work, which takes a product of forces and displacements. Also, impulse will have an impact on the motion of the object, as work did. But there are also many differences between these two quantities.
The first difference between impulse and work is that they obviously represent different physical quantities, because they have different units. While work has units of energy which we measure in Joules (or Newton-meters), impulse has units of force-times-time, measured in Newton-seconds. A second difference is that the impulse integral (mercifully) is not a line integral – there is no "path" to concern ourselves with when computing impulse. And third, because there is no dot product involved with the impulse integral, the result is a vector, in contrast to work, which is a scalar.
Definition of Momentum
The definition of impulse is not the end of the story, any more than the definition of work was. It needs to be related to the effect it has on the motion of the object. In the case of work, this relationship was expressed as the work-energy theorem:
\[\begin{array}{l} \text{actions of pushes and pulls} && = && W_{tot}\left(A\rightarrow B\right) \\ && = && \int \limits_A^B \overrightarrow F_{net} \cdot \overrightarrow {dl} \\ && = && \frac{1}{2} mv_B^2 - \frac{1}{2} mv_A^2 \\ && = && \Delta KE \\ && = && \text{effect of pushes and pulls} \end{array} \]
For the case of impulse, we find this relationship again by coming back to Newton's second law, and noting that the integral of acceleration is velocity:
We call the quantity \(\overrightarrow p_{cm}\) the momentum of the collection of particles on which the net force is acting, defined in terms of the total mass of the collection of particles and the velocity (magnitude and direction) of the collection's center of mass. As we saw in chapter 2, Newton's 2nd law works for any collection of particles, whether they form a solid object or are completely non-interacting, like a gas. So since this result is derived from the 2nd law, the same is true here. While this definition applies to a collection of particles, it is useful to define this same quantity for individual particles as well.
Definition: Momentum
\[\overrightarrow p \equiv m \overrightarrow v\nonumber \]
It turns out that if we do happen to have a collection of particles, each with their own individual momentum, then computing the collective momentum \(\overrightarrow p_{cm}\) is a simple matter of summing the individual momenta:
\[\vec p_1+\vec p_2 + \dots = m_1\vec v_1+m_2\vec v_2+\dots=\left(m_1+m_2+\dots\right)\frac{m_1\vec v_1+m_2\vec v_2+\dots}{\left(m_1+m_2+\dots\right)}=M_{tot}\vec v_{cm}\]
Equation 4.1.3 is known as the impulse-momentum theorem. Like kinetic energy, momentum is related to the motion of the object (and the mass), but besides being a different function of mass and velocity than kinetic energy, it is also different in that momentum is a vector while kinetic energy is not. This means that the total impulse can lead to a change in the magnitude or direction (or both) of the momentum vector.
The astute reader will undoubtedly realize that all we have really done here is to introduce a new vector, and use it to repackage Newton's 2nd law. Indeed, we can rewrite the 2nd law thus:\[ \overrightarrow F_{net} = m \overrightarrow a_{cm} = m \dfrac{d}{dt}\overrightarrow v_{cm} = \dfrac{d}{dt}\left(m\overrightarrow v_{cm}\right) = \dfrac{d}{dt}\overrightarrow p_{cm} \]
The Link to Internal Energy
Given that we are making comparisons of work with impulse and momentum with kinetic energy, it is useful to point out a direct mathematical relationship, which not only points out the difference between the two quantities, but will also be quite useful later on. For an individual particle we have:
Two pairs of identical blocks on identical springs are side-by-side as shown in the diagram below. They are set into motion such that just as they reach their (equal) maximum displacements toward each other, they barely come into contact (there is no collision – their springs stop them just as they touch). When they contact, one of the blocks is transferred to the other, and their motion continues.
- Analysis
-
Let's start by defining two separate systems here: One that includes the left spring and the blocks it is moving, and one that includes the right spring and the block(s) it is moving. At the moment the blocks touch, all of the potential energy of both systems is stored in the stretch of their respective springs. Losing or adding a block has no effect on this energy, because at the time of the exchange the blocks are not moving, and therefore have no kinetic energy.
So the left side has the same total energy with three blocks as it previously had with two blocks, and the right side has the same total energy that it started with as well. What does that tell us about how the motions of the two systems change, if at all, after the block exchange? We can start by asking about the maximum speeds the blocks attain on each side, before and after. First of all, this occurs when the spring reaches its equilibrium position, because at that moment the potential energy is as low as it can be. Both before and after, this maximum kinetic energy is the same, but the masses are different, so the speeds will not be the same. In order for the kinetic energy to be the same with three blocks as with two, the ratio of the velocities must be:
\[\begin{array}{l} \text{left spring:} && \frac{1}{2}\left(2m\right)v_{\text{max before}}^2=\frac{1}{2}\left(3m\right)v_{\text{max after}}^2 && \Rightarrow && v_{\text{max after}}=\sqrt{\frac{2}{3}}\;v_{\text{max before}}\\ \text {right spring:} && \frac{1}{2}\left(2m\right)v_{\text{max before}}^2=\frac{1}{2}\left(1m\right)v_{\text{max after}}^2 && \Rightarrow && v_{\text{max after}}=\sqrt{2}\;v_{\text{max before}} \end{array}\nonumber\]
Note that this means that the left side is moving slower overall than the right side, and they will not complete a full cycle at the same time. Even though each side will reach far enough at their maximum spring stretched for the blocks to once again touch, the motions are no longer synchronized, so the blocks will not touch again.
One can also compare the momentum of the left side blocks at the equilibrium point to the momentum of the right side blocks at their equilibrium point. The kinetic energies are the same, so since the left side has 3 times the mass, we have:
\[\text{at equilibrium: }{KE}_{\text{left}}={KE}_{\text{right}}\;\;\;\Rightarrow\;\;\;\frac{p_{\text{left}}^2}{2\left(3m\right)}=\frac{p_{\text{right}}^2}{2\left(1m\right)}\;\;\;\Rightarrow\;\;\;p_{\text{left}}=\sqrt{3}\;p_{\text{right}}\nonumber\]
Consider now a collection of particles, each with their own momentum (for simplicity, we will assume that the collection is an ideal gas – the particles are not interacting with each other). Above, we showed that the total momentum of the collection is just the sum of the momenta of the individual particles. But in the previous chapter, we found that the sum of the individual particle kinetic energies is not equal to the collection's (center of mass) kinetic energy. This is easiest to see in the center of mass reference frame. In this frame, \(\vec v_{cm}=0\), which means that the collection's total momentum is zero. But the individual particles can be moving in this frame, so the sum of their kinetic energies is not zero. The difference between adding kinetic energies and momenta is that the kinetic energy of every particle is positive, but momentum vectors of multiple particles add like vectors, and can cancel to zero.
The short summary of this is that in the center of mass frame there is zero momentum for the collection, but there is still non-zero internal energy. Let's see how it works mathematically with a simple two-particle system, like we discussed in Section 3.2. We start by defining the momentum of the particle as \(\vec p_1\) and \(\vec p_2\). The total momentum of the two-particle collection is just the sum of these:
\[\vec p_{cm} = \vec p_1+\vec p_2\]
The total energy of this group of particles is just the sum of their kinetic energies:
\[E_{tot} = \dfrac{p_1^2}{2m_1}+\dfrac{p_2^2}{2m_2}\]
The kinetic energy of the group (defined in terms of its total mass and center-of-mass speed) is:
\[KE=\dfrac{p_{cm}^2}{2\left(m_1+m_2\right)}=\dfrac{\left(\vec p_{cm}\cdot \vec p_{cm}\right)}{2\left(m_1+m_2\right)}=\dfrac{\left(\vec p_1+\vec p_2\right)\cdot\left(\vec p_1+\vec p_2\right)}{2\left(m_1+m_2\right)}=\dfrac{\left(p_1^2+p_2^2+2\vec p_1\cdot\vec p_2\right)}{2\left(m_1+m_2\right)}\]
The internal energy is the total energy minus the group's (center of mass) kinetic energy, so using the last two equations we get, after some algebra:
\[E_{int} = E_{tot} - KE = \frac{1}{2\left(m_1+m_2\right)}\left[\frac{m_2}{m_1}p_1^2+\frac{m_1}{m_2}p_2^2-2\vec p_1\cdot\vec p_2\right]\]
The general features of this equation match what we already know about internal energy for a two-particle combination. For example, if the particles are moving in the same direction, then they are moving slower in the center of mass frame, and the internal energy is smaller than if they happened to be moving the same speeds toward each other. This fact is reflected in the last term above – if \(\vec p_1\) and \(\vec p_2\) are pointing in the same direction, then the dot product is positive, and the minus sign indicates that the internal energy is reduced. If the two momentum vector directions are in opposite directions, then the dot product is negative, and the last term increases the internal energy.
One thing that is not obvious is whether this equation allows for a negative internal energy for some choice of momentum vectors. This is of course impossible physically, as the smallest the internal energy can be is zero, when the particles are stationary relative to each other. Let's check this in the following way: Start with one particle having a momentum of \(\vec p_1\), and then let the internal energy be a function of the momentum \(\vec p_2\) that we choose for the second particle. Then minimize the internal energy function with respect to this variable. Obviously the minimum will occur when the negative term is as large as possible, and this occurs when \(\vec p_1\cdot\vec p_2 = p_1p_2\), so we have:
\[E_{int}\left(p_2\right) = \frac{1}{2\left(m_1+m_2\right)}\left[\frac{m_2}{m_1}p_1^2+\frac{m_1}{m_2}p_2^2-2p_1p_2\right]\]
Taking a derivative of this function with respect to \(p_2\) (remember, \(p_1\) was selected at the beginning, so it is not varying) and setting it equal to zero gives:
\[0=\frac{dE_{int}}{dp_2} = \frac{1}{2\left(m_1+m_2\right)}\left[2\frac{m_1}{m_2}p_2-2p_1\right]\;\;\;\Rightarrow\;\;\;\frac{m_1}{m_2}p_2=p_1\]
Noting that \(\frac{p}{m}=v\), this result gives that the internal energy is a minimum when \(v_1=v_2\) – both particles moving at the same speed in the same direction. We can confirm by plugging this back in that this gives us the expected result of zero internal energy, so indeed it can never be negative.
Systems and Momentum Conservation
Let's return to following the trajectory of our discussion of work-energy, by revisiting the notion of a system. As before, we define a system as an arbitrarily-grouped collection of objects (which themselves can have internal energies), that can experience forces between themselves, or from outside the system. Previously we said that forces between objects within the system were responsible for internal work and forces exerted on objects within the system from outside provide external work. We will now similarly define internal impulse as coming from forces between objects within the system, and external impulse as coming from objects outside the system.
When it comes to forces between objects within our defined system, we know that the work done on one object does not cancel the work done on the other object. If the internal force is conservative, then the non-zero total work done between the objects can be accounted-for through a change of potential energy. If the internal force is non-conservative, then the non-zero total work done between the objects can be accounted-for through a change of thermal energy. Is there an analogous process for impulse?
To answer this question, we need to determine whether impulses internal to a system don't cancel out, as in the case of work. We again start with Newton's 3rd law, which ensures that the two forces involved in creating the pair of impulses are equal-and-opposite. Impulse vectors have the same directions as their associated force vectors, so the 3rd law pair of forces results in a pair of impulses that are in opposite directions. But what about the magnitudes? Well, the force magnitudes are equal thanks to the third law, so all that remains is the time interval. There is never a moment when a force is acting that its third law pair isn't also acting, so the time intervals are the same. This leads to the following very important result: All of the impulses internal to a system cancel each other out. This means that there is no momentum analog to potential or thermal energy within a system. There is only momentum, and if the system experiences no external impulses, then momentum is conserved for the system. Comparing to what we got for energy, it looks like this:
\[\begin{array}{c} \textbf{work-energy}&\;\;\;\;\;\;&\textbf{impulse-momentum} \\ W_{ext} = \Delta KE \underbrace{- W_{cons} - W_{non - cons}}_{from\;internal\;forces}&\;\;\;\;\;\;&\overrightarrow J_{ext} = \Delta \overrightarrow p_{cm} \underbrace { - \overrightarrow J_{cons} - \overrightarrow J_{non - cons}}_{from\;internal\;forces} \\ W_{ext} = \Delta KE + \Delta PE + \Delta E_{thermal}&\;\;\;\;\;\;&\overrightarrow J_{ext} = \Delta \overrightarrow p_{cm} + 0 \;\;\;\; + \; 0\;\;\;\;\;\;\;\;\;\;\; \end{array}\]
There are two important features of this result:
- It doesn't matter what forces are acting internally. The result we obtained made no mention of whether the internal force was conservative or non-conservative – all forces satisfy Newton's third law, and the pairs act for equal periods of time, so the impulses cancel regardless of the nature of the force.
- The quantity (momentum) that is conserved within the closed system is a vector. This means that adding up all of the momentum vectors of a system at one point in time, then doing so again at another point in time, will give the same total vector in both cases, if the system is isolated from external impulses. This means that the total magnitude and direction don't change, or equivalently that the components measured in a given coordinate system don't change.
Conceptual Question
Two blocks of different masses are attached to identical springs that are horizontal to the frictionless surface on which the block rests. If the springs are compressed the same distance and the blocks are released from rest, how do the following quantities compare for the two blocks when they reach the equilibrium point?
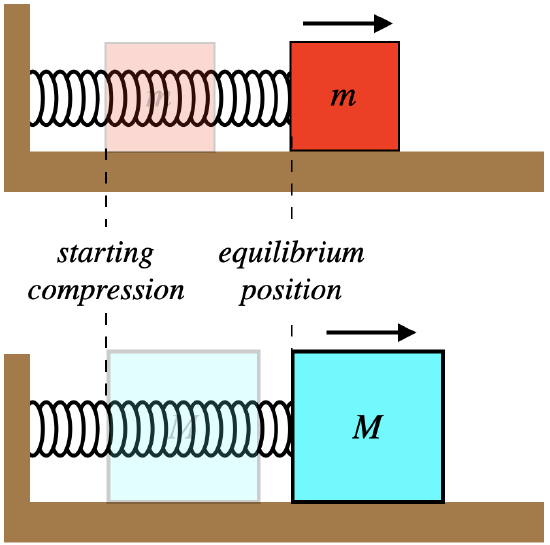
- kinetic energy
- momentum
- velocity
- Solution
-
a. The springs are stretched an equal amount, which means they both store the same potential energy. That means that when they get to the equilibrium point where they both have zero potential energy, they must have the same kinetic energy, since the mechanical energy is conserved.
b. We can determine the difference in momenta for the two blocks in two ways. First, we can consider the impulse given to each block by the spring. In the case of the more massive block, the spring force will accelerate it less, which means it will take longer to get to the equilibrium point. At every point during their journeys, the two blocks experience the same amount of force, but since the time interval for the heavier block is longer, it must experience the greater impulse. Therefore the heavier block gains more momentum, and since both blocks started with zero momentum, the heavier block must have more momentum at the equilibrium point. The second solution is much simpler: We already know that the two blocks end with the same \(KE\), so since \(KE=p^2/2m\), the block with the greater mass must have more momentum.
c. With the same kinetic energy, using \(KE=\frac{1}{2}mv^2\), we see that the block with the greater mass must have the lower velocity.
The moral of this story: Although we tend to use kinetic energy, momentum, and velocity as proxies for motion, they are all quite different quantities.
Partial Momentum Conservation
We have to give some extra thought to what we mean by a conserved vector. Since a vector has both magnitude and direction, then to be conserved, both of those properties must remain unchanged. An equivalent way of saying this is that for the vector to be conserved, every component of that vector must be individually conserved. If the full momentum vector is not conserved, it is still possible for one or two of its components to be conserved, if the components of the external impulse in those directions is zero. So for example, a projectile (with no air resistance) conserves momentum in the two horizontal directions, but not in the vertical direction. This allows us to use momentum conservation to solve a much broader range of problems than if we can only consider complete momentum conservation.