3.2: Work and Energy for Collections of Particles
- Page ID
- 63365
Internal Energy
We now wish to extend our results from the previous section beyond just single particles. We want to ultimately talk about macroscopic objects, but of course these are merely collections of particles. If we choose a model where this macroscopic collection of particles are held rigidly in place, without the ability to move independently from each other, then such an object can be treated in exactly the same way as an individual particle (assuming the object doesn't rotate). We will actually do this quite a lot in the coming pages, but for now we want to look at what happens if the particles in our collection can move independently of each other.
We will start by looking a little closer at kinetic energy. When we first talked about force, we made very clear that force was not a quantity possessed by an object – it is an interaction between two objects. Let's ask the same question of kinetic energy – is kinetic energy a property that "belongs" to a particle? At first blush, the answer would appear to be yes. The particle has a well-defined mass and speed, so since \(KE=\frac{1}{2}mv^2\), it seems like we can attribute this quantity to the particle itself – there is no interaction or cause/effect here as there was for force.
But alas, there is a problem with attributing this quantity solely to the particle, and that has to do with the observer that measures the kinetic energy. If it was a property that belonged exclusively to the particle, then everyone that measures it for the same particle should get the same number. But clearly this is not the case. Imagine that Ann watches a particle with mass \(m\) and speed \(v\) fly by. She says, "That particle has a kinetic energy of \(\frac{1}{2}mv^2\)." But Bob, who is moving past Ann, traveling along with the particle, measures the speed of the particle to be zero, and claims that the particle's kinetic energy is zero! Kinetic energy is not a property we can attribute to the particle if different observers measure different values for it. Clearly there is always a frame (the one that moves along with the particle) for which the kinetic energy is zero.
Now let's suppose we have a collection two non-interacting particles. The total energy of this two-particle collection is just the sum of the kinetic energies of these particles. Does there exist a frame in which the energy of this collection is zero? In general, the answer is no! If the two particles happen to be moving at the same speed in the same direction, then yes, jumping over to the frame common to both of these particles will result in both particles being stationary. But in any case where the two particles are moving relative to each other, then no such "zero total energy" frame exists. If you jump on the frame of one particle, then it is stationary, but the other is moving.
Okay then, let's see if we can determine, for the simplest case of two particles, what frame results in the lowest amount of total energy, given that it is in general not equal to zero. It is probably not clear why we would care to know this yet, but hang in there...
Figure 3.2.1 – Two Particle Collection (Non-Interacting)
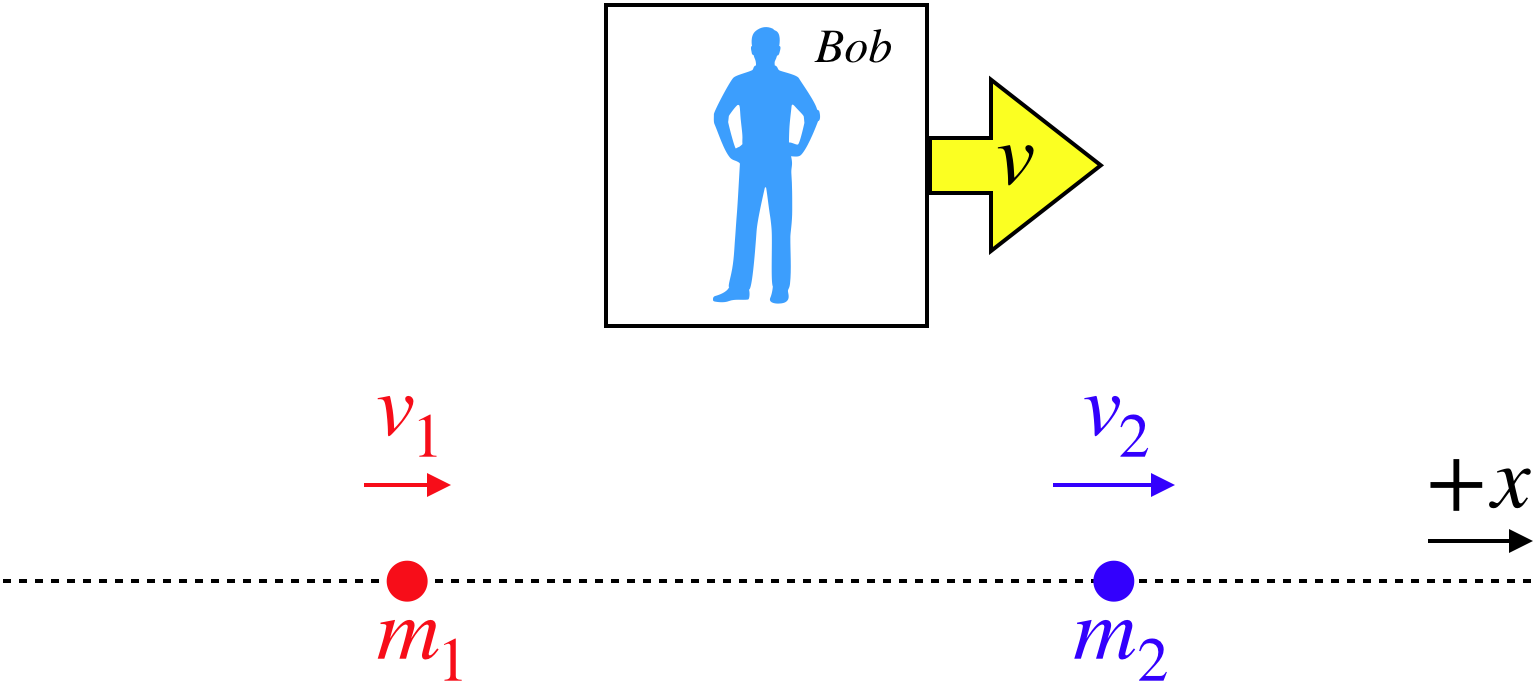
The figure shows a very simple case of two particles moving along a line at different speeds (shown from our perspective), and another observer (Bob) moving along the same direction. If Bob is moving slower than the slowest particle, then he will see speeds for the particles that are both slower than what we see from our perspective. Bob will measure a smaller energy for this two-particle collection than what we measure, since both particles are moving slower. It is easy to write mathematically what energy Bob sees. Particle #1 is moving (according to him) at a speed of \(v_1-v\), and particle #2 at a speed of \(v_2-v\), so:
\[E\left(\text{seen by Bob}\right)=\frac{1}{2}m_1\left(v_1-v\right)^2+\frac{1}{2}m_2\left(v_2-v\right)^2\]
Now Bob (by changing speeds) can choose to look at these particles from any frame he likes, which means that the energy of the two-particle collection is a function of the speed \(v\) (relative to us) that he chooses. If we want to know the minimum energy one can measure for this two-particle combination, one only needs to minimize the function \(E\left(v\right)\) with respect to \(v\):
\[0=\dfrac{dE}{dv} = -m_1\left(v_1-v\right)-m_2\left(v_2-v\right)\;\;\;\Rightarrow\;\;\; v=\dfrac{m_1v_1+m_2v_2}{m_1+m_2}\]
This looks vaguely familiar... If we take a time derivative of the position of the center of mass of two particles aligned on the \(x\)-axis (Equation 2.4.8), we get the same expression:
So this is the velocity of the center of mass of the two-particle combination! Bob measures the minimum energy for the collection when he is moving along with the collection as a whole, i.e. in the same frame as its center of mass. Put another way, from Bob's perspective, while he sees the individual particles moving, according to him, the combined two-particle group is not.
Let's answer another question: For those of us not in the center-of-mass frame of the collection like Bob, how much greater do we measure the collection's energy to be? We can calculate this simply by subtracting the energy Bob measures from the amount we measure:
\[\text{extra energy we measure above the minimum}=\left[\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\right]-\left[\frac{1}{2}m_1\left(v_1-v_{cm}\right)^2+\frac{1}{2}m_2\left(v_2-v_{cm}\right)^2\right]\]
The reader is encouraged to plow through the algebra here to obtain the final result, which is surprisingly simple:
\[\text{extra energy we measure above the minimum}=\frac{1}{2}\left(m_1+m_2\right)v_{cm}^2\]
But wait, this is just the kinetic energy equation for a single object of mass \(M=m_1+m_2\) and speed \(v_{cm}\). The details related to the fact that the "object" is made out of two moving particles is utterly ignored in this expression. This completes a very simple, intuitive picture for how we do the energy accounting for a collection of particles:
\[E_{tot}\left(\text{collection of particles}\right) = KE_{collection} + E_{internal}\;,\]
where \(KE_{collection}\) is the kinetic energy of the collection as a single entity, calculated from its total mass and center of mass velocity, and \(E_{internal}\) is the internal energy of the collection, defined as the sum of the kinetic energies of the particles comprising the collection, as measured in the center of mass frame of reference. Notice that the internal energy of a collection is a feature of the full group of particles as an entity, no matter who is looking at it. The total energy then only changes with observer because the whole group's KE changes when the perspective is changed.
A few additional comments need to be added here:
- This definition of internal energy depends upon the particles not interacting with each other. As such, it works pretty well for something we will call "ideal gases" when we get to Physics 9B. We will later make a small alteration to this definition when the particles within the collection push and pull on each other, but the idea of internal energy will endure.
- It should be clear that if we use a model for a macroscopic object that consists of particles which are rigidly arranged, this model allows for no internal energy. In these cases, the rigid object can be treated as if it was just a single particle, which simplifies calculations. This model is useful as an approximation (just like assuming pulleys are massless, surfaces are frictionless, or there is no air resistance), but in reality all objects are made of particles that can move, and therefore all objects possess some internal energy.
- While particles within the collection of a rigid object that rotates are moving relative to each other, in a future chapter we will introduce another type of kinetic energy (i.e. "rotational KE") for the object as a whole, which is not considered part of the internal energy.
Three identical particles, A, B, and C are positioned at the vertices of an equilateral triangle. Particle A remains at rest at the origin, while particles B and C move directly away from particle A at equal speeds along the lines defined by the triangle, as shown in the diagram.
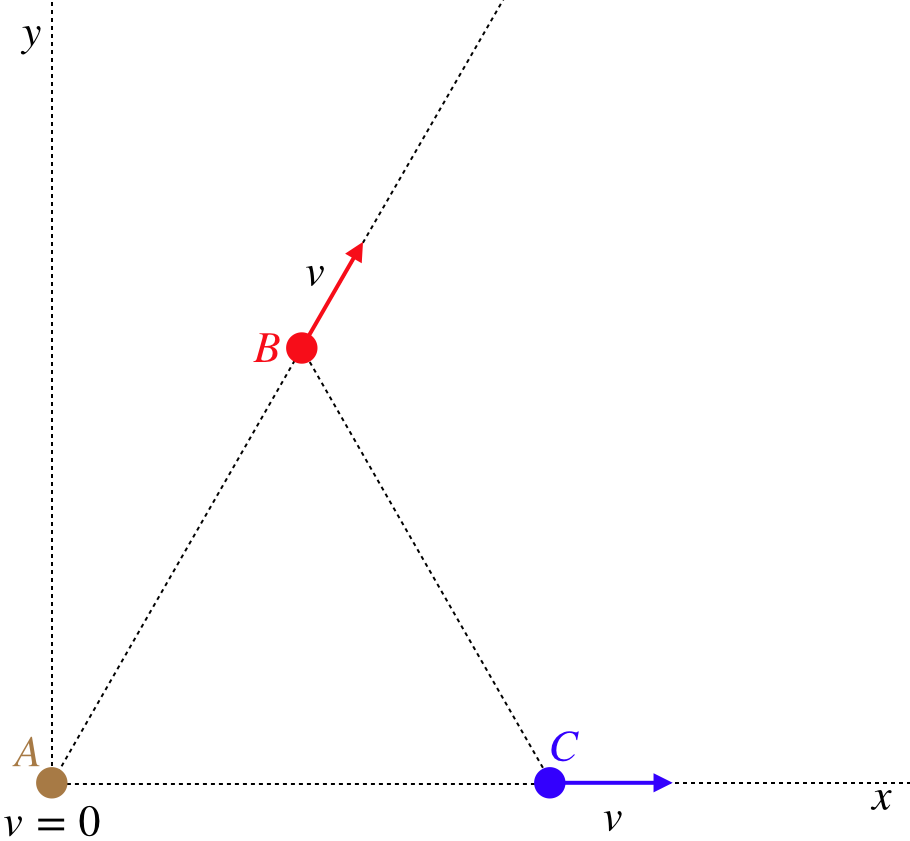
- Analysis
-
We can immediately determine the energy in the three-particle collection measured in the frame shown, as it is just the sum of the kinetic energies of the two moving particles. They are identical in mass, and are moving at equal speeds, so:
\[E_{tot\; ABC}=\frac{1}{2}m_Av_A^2+\frac{1}{2}m_Bv_B^2+\frac{1}{2}m_Cv_C^2=0+\frac{1}{2}mv^2+\frac{1}{2}mv^2=mv^2\nonumber\]
The particles are moving relative to each other, so this collection must have some internal energy. But this internal energy must be less than \(mv^2\), because the frame shown is not the center of mass frame. How do we know this? Well, the particles at this moment lie on the vertices of an equilateral triangle, and particles B and C continue moving along the lines defined by that triangle at equal speeds, so at any later time they must still lie on the vertices of an equilateral triangle (each is always the same distance from particle A as the other, and the angle at particle A remains \(60^o\)). The center of mass for three equal-mass particles that form an equilateral triangle is obviously going to be the geometric center of that triangle. But this triangle is growing with time, so the geometric center is moving away from the origin, along a line that forms a \(30^o\) angle with the \(x\)-axis. So the center of mass is moving relative to the frame defined by the diagram.
From the geometry given and the fact that all three particles have the same mass, we can determine the precise velocity of the center of mass measured in the diagramed frame in terms of v:
\[\begin{array}{l} v_{cm\;x} = \dfrac{m_Av_{Ax}+m_Bv_{Bx}+m_Cv_{Cx}}{m_A+m_B+m_C}=\dfrac{0+mv\cos 60^o+mv}{3m}=\dfrac{v}{2}\\v_{cm\;y} = \dfrac{m_Av_{Ay}+m_Bv_{By}+m_Cv_{Cy}}{m_A+m_B+m_C}=\dfrac{0+mv\sin 60^o+0}{3m}=\dfrac{v}{2\sqrt{3}}\end{array}\nonumber\]
We can use this result to determine the speed of the particles relative to the center of mass of the collection. We have a cool trick at our disposal here. Clearly due to the symmetry, every particle is moving away from the center of mass at an equal speed (imagine standing at the center of mass, stationary in your frame, and watching all the particles move away from you as they remain in an equilateral triangle). But there is one particle whose speed relative to the center of mass is easy to compute: particle A. In the frame of the diagram, particle A is not moving, and the center of mass is moving away from it at some speed, so if we change to the rest frame of the center of mass, particle A must be moving away from the center of mass at the same speed. We therefore conclude that every particle is moving away from the center of mass at a speed of:
\[v_{cm\;frame}=\sqrt{v_x^2+v_y^2}=\dfrac{v}{\sqrt{3}}\nonumber\]
And now that we know how fast every particle is moving in the center of mass frame, we know the internal energy of the group:
\[E_{internal}=3\left(\frac{1}{2}mv_{cm\;frame}^2\right)=\frac{1}{2}mv^2\nonumber\]
The kinetic energy of the full collection in the diagrammed frame can be found either by subtracting the internal energy (\(\frac{1}{2}mv^2\)) from the total energy (\(mv^2\)), or by plugging the total mass (\(3m\) and the center of mass velocity (\(\frac{v}{\sqrt{3}}\)) into the KE formula (\(\frac{1}{2}m_{tot}v_{cm}^2\)). Both clearly give the same answer.
Work Done on Collections of Particles
Next we will look at the effect of work on collections of particles. We once again choose a very simple model to start with – two particles start at rest on the \(x\)-axis, and a force is applied to one of them, speeding it up along that axis. The force remains constant in both magnitude and direction, and is applied until the particle is displaced by a distance of \(\Delta x\).
Figure 3.2.2 – Work Done on Two Particle Group
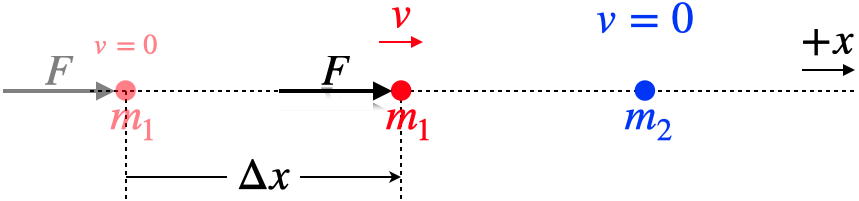
We know exactly how much energy has been added to this collection. It started with zero, and the amount of work that was done equals the kinetic energy change of particle #1. Given that particle #1 started at rest and particle #2 remains at rest, its change of kinetic energy constitutes all of the energy given to the particle collection. But now we know that since the particles within the group are in relative motion, some of this energy given to the two-particle entity goes into internal energy, which means that not all the energy added to the collection by this work goes into its collective (center of mass) kinetic energy. Summarizing:
\[\text{energy added to collection} = F\Delta x = \frac{1}{2}m_1v^2=KE_{collection} + E_{int}\]
So it would appear that the work-energy theorem only applies to individual particles, since the work done does not equal the change in the full group's kinetic energy. But appearances are deceiving! While \(F\Delta x\) is the work done on one particle in the collection, it is not the work done on the group as a whole, because the displacement \(\Delta x\) is not equal to the displacement of the group. The group's displacement is the change in the position of its center of mass, and the position of the center of mass moves less than particle #1 does. This shorter displacement of the two-particle collection results in less work done on it than the same force does on the individual particle, and the difference is exactly equal to the internal energy. In other words, the work done in moving the center of mass of the group exactly equals the change in the group's kinetic energy.
Exercise
Show that the above statement is true (for the two-particle example above): The work done moving the group's center of mass equals the change in its kinetic energy, confirming the work-energy theorem for collection of particles.
- Solution
-
The change of the position of the center of mass is:
\[\Delta x_{cm} = \dfrac{m_1\Delta x_1+m_2\Delta x_2}{m_1+m_2}=\dfrac{m_1\Delta x+0}{m_1+m_2}=\dfrac{m_1}{m_1+m_2}\Delta x\nonumber\]
So the work done on the group is:
\[W\left(\text{on group}\right)=F\Delta x_{cm} = \left(\dfrac{m_1}{m_1+m_2}\right) F\Delta x = \left(\dfrac{m_1}{m_1+m_2}\right)\frac{1}{2}m_1v^2\nonumber\]
Now let's calculate the kinetic energy change of the group (it changes from zero):
\[KE_{sys}=\frac{1}{2}\left(m_1+m_2\right)v_{cm}^2 = \frac{1}{2}\left(m_1+m_2\right)\left(\dfrac{m_1v+0}{m_1+m_2}\right)^2 =\left(\dfrac{m_1}{m_1+m_2}\right)\frac{1}{2}m_1v^2 \nonumber\]
They are indeed equal.
It is interesting to note that if equal forces act on each of the two particles in opposite directions, then they both speed up, but of course in this case the net force on the two-particle collection is zero, which means that the center of mass doesn't move. In this case, all of the energy goes into the internal energy. As a general rule, combinations of forces that stretch or compress objects (without accelerating their centers of mass) add to the internal energy of that object. This observation gives us a hint about how to deal with internal forces (forces between particles in the same object) later on.
While everything we have shown here has applied to a specific case of a force acting on a single particle of a two-particle group in one dimension, the results apply much more generally.