4.2: Center of Mass
( \newcommand{\kernel}{\mathrm{null}\,}\)
Center of Mass Again
It should be clear by now how important the concept of center of mass is in classical mechanics. First it appeared in Newton's 2nd law, then in the discussion of internal energy, and now again in the topic of momentum. So far our only exposure to center of mass as a calculated quantity comes from Equation 2.4.10, which we will repeat here:
→rcm=xcmˆi+ycmˆj+zcmˆk=[m1x1+m2x2+…]ˆi+[m1y1+m2y2+…]ˆj+[m1z1+m2z2+…]ˆkM=m1[x1ˆi+y1ˆj+z1ˆk]+m2[x2ˆi+y2ˆj+z2ˆk]+…M=m1→r1+m2→r2+…M
In this chapter, we will have a closer look at this quantity, to see how we can compute it for cases more general than a collection of a few point particles. In particular, we are going to look at objects that we treat as continuous distributions of mass, rather than collections of discrete particles. Of course, real matter is a collection of discrete particles, but a continuous model is much more practical to handle mathematically.
Center of Mass of a Collection of Objects
Suppose now we want to know the center of mass of multiple extended objects, where all the heavy-lifting has already been done – the centers of mass of the objects are already known (see below for how to do this heavy-lifting). How do we determine the center of mass of such a system? It turns out to be pretty easy when you know the locations of the centers of mass of the two objects – just treat them as if they are point particles with all of their mass concentrated at their own centers of mass, and then do the calculation above.
Figure 4.2.2 – Center of Mass for Two extended objects
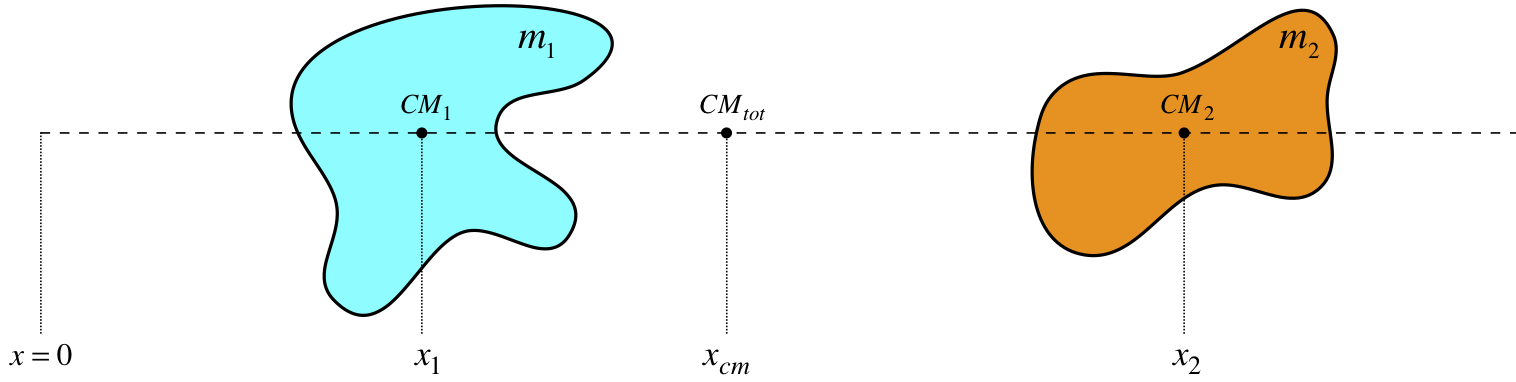
For proof of this, let's treat two extended objects (A and B) as collections of lots of point particles (atoms, if you like), and write down their centers of mass (measured from a common origin) in terms of the masses and positions of their atoms.
→rcmA=m1A→r1A+m2A→r2A+…MA→rcmB=m1B→r1B+m2B→r2B+…MB}⟺→rcm=MA→rcmA+MB→rcmBMA+MB
The left-hand side equations are those of the center of mass for each object in terms of its atoms' masses and positions. The right-hand side gives the center of mass of the two-object system in terms of the masses of the objects and the positions of their individual centers of mass. When the expressions for →rcmA and →rcmB from the left side are plugged into the right-hand side equation, then all the atoms of both objects are come together into a single center of mass formula, as if they were part of a single system with total mass MA+MB, proving the contention above.
Exercise
Two thin circular disks made from the same material lie flat on a horizontal surface, with their outer edges in contact with each other. One disk has a larger radius (R) than the other (r), and have equal thicknesses. Find how far the center of mass of the two-disk system lies from the center of the larger disk.
- Solution
-
The disks are made from the same uniform material, so they have equal mass densities. That means that the mass of the larger disk is larger than that of the smaller disk by the same factor as the ratio of their areas. That is, if the larger disk has twice the area of the smaller one, then it has twice as much mass. We therefore have the following relationship between the masses and radii of the disks:
Mm=πR2πr2⇒M=R2r2m
Let's choose the center of the larger disk as the origin, and have the center of the other disk lie on the +x-axis. The disks are uniform, so their individual centers of mass lie at their geometric centers, and we can compute the center of mass of the system by treating the disks as point masses located at these centers. The distance of the center of mass from the origin is what we are looking for, so:
xcm=Mx1+mx2M+m=M(0)+m(R+r)M+m=m(R+r)R2r2m+m=(R+r)r2R2+r2
We can double-check this answer by looking at an obvious special case: R=r. If the disks are identical, then the center of mass must be halfway between their centers, which is the point where they are in contact, a distance R from the center of the larger disk. Plugging in R for r indeed gives this answer.
Center of Mass of Continuous Objects
We now turn to the problem of computing the position of the center of mass of an object whose distribution of mass is known. What follows is pure math, but it is important math that returns over and over in physics.
Alert
The important thing to gain from this discussion is to understand how the set-up process works. It culminates in an integral, but performing the integral is mere busywork compared to the task of setting it up. It's easy to be overwhelmed by the thought of the integral that is being constructed, but if you understand each step that leads up to it (and don't try to just jump to an answer that looks like something you have seen before), it will go fine.
We will keep this simple by restricting ourselves to objects for which the position of the center of mass in two of the three dimensions is obvious, which means we don't need to concern ourselves with the whole vector described in Equation 2.4.10 – just the x-component will do. A good model for this is a simple thin, cylindrical rod. This rod's mass distribution is completely cylindrically symmetric, which means that the center of mass lies on the axis passing through its center. But the mass distribution as a function of position on this axis may not be uniform. For example, it may be more dense on one end than on the other. Put another way, the particles located within the rod may be packed together more tightly in one region of the rod than in another, which means that the center of mass will not necessarily lie at the point halfway between the ends.
We need to say a few words about mass density before we proceed. Density is a measure of how closely-packed in space a quantity of something is. This quantity can be many different things. Here we will be considering mass, but in later physics classes you will deal with density of electric charge (and even, bizarrely, probability!). A uniform density for a region in space means that the quantity (whatever it happens to be) is evenly-distributed everywhere within that region. The way we define an average density for a region in space is to add up how much "stuff" is there, and then divide it by the total space it occupies. This gives an average density, but of course densities can vary from one point in space to another, in which case a density function is defined. We will deal with only the simplest variable densities here. As we will mainly be looking at thin rods for our examples, we will only consider densities that might vary along the length of the rod – this simplifies the process to a single dimension.
The mass density function in this case is a function of a single variable, has units of kgm, and is called a linear mass density. This mass density function is typically denoted as λ(x). If it is uniform, then the function is a constant λ, and the amount of mass m within a given length l is simply given by:
If the density is not uniform, then it is only a constant over an infinitesimal length dx, so the equation above can only apply to a tiny piece of mass dm, and the relationship is different at every position x because the density is different at every position:
Now that we can write down how much mass is at every position, we are ready to do our calculation. We begin by drawing a diagram with the rod in a coordinate system along the x-axis such that one end is at the origin and the other is at x=L. The figure below provides a fully-labeled diagram that is very helpful for solving such problems.


