Sample Problems

All of the problems below have had their basic features discussed in an "Analyze This" box in this chapter. This means that the solutions provided here are incomplete, as they will refer back to the analysis performed for information (i.e. the full solution is essentially split between the analysis earlier and details here). If you have not yet spent time working on (not simply reading!) the analysis of these situations, these sample problems will be of little benefit to your studies.

Problem 6.1

Two uniform disks are free to rotate frictionlessly around vertical axles. Initially one of the disks is rotating, while the other is not.  They are then brought together so that their outer edges rub against each other. Kinetic friction between the two rubbing surfaces slows down disk #1, while speeding up disk #2.  This continues until their rotational speeds are such that no slipping occurs between the two surfaces. With kinetic friction no longer present, they continue with constant rotational motion from this point forward.

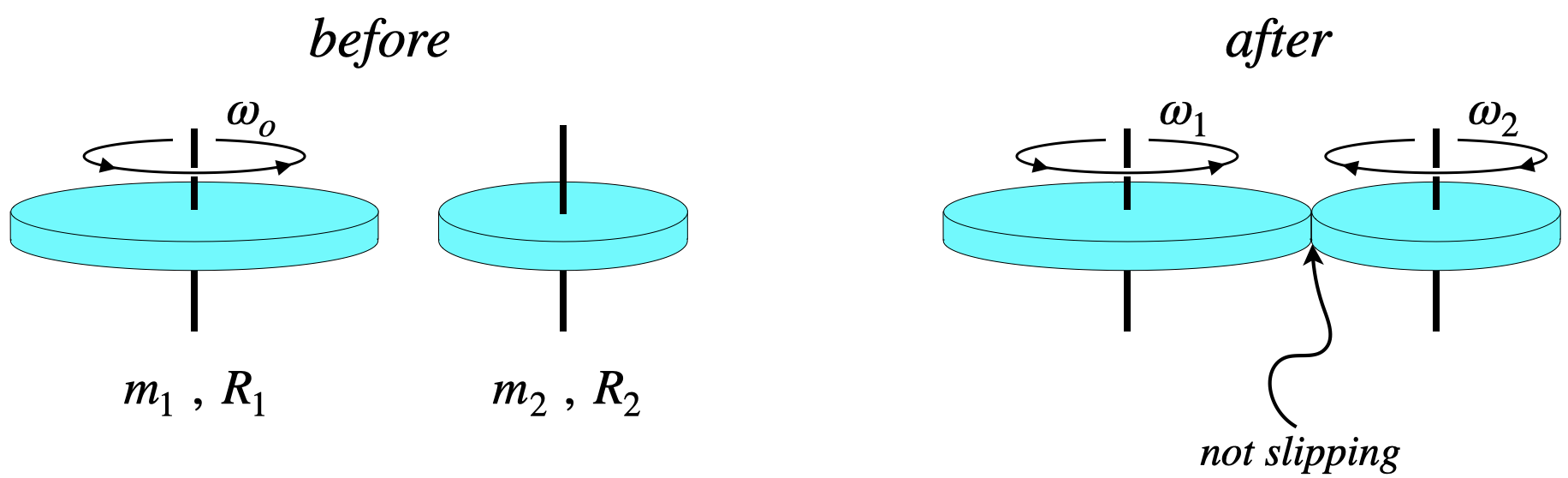
The disks are the same thickness and are made from the same material. Disk #1 has a radius that is twice that of disk #2. Find the percentage of the starting kinetic energy that is converted to thermal during the period that the edges of the disks rub against each other.

Solution

With twice the radius, the larger disk has four times the horizontal surface area, and with equal thicknesses, then means that there is four times as much mass for the larger disk than the smaller one. Calling the smaller disk's radius "\(R\)" and mass "\(m\)", we have:

\[R_1=2R~,~~R_2=R~~~~m_1=4m~,~~m_2=m\nonumber\]

To find the thermal energy, we just need to subtract the "after" kinetic energy from the "before" kinetic energy. From the analysis, we have the "after" rotational speeds of the disks in terms of initial speed of disk #1, so we have:

\[KE_{1~after}=\frac{1}{2}I_1\omega_1^2=\frac{1}{2}\left[\frac{1}{2}m_1R_1^2\right]\left(\frac{m_1}{m_1+m_2}\right)^2\omega_o^2=\frac{1}{2}\left[\frac{1}{2}\left(4m\right)\left(2R\right)^2\right]\left(\frac{4m}{4m+m}\right)^2\omega_o^2=\frac{64}{25}mR^2\omega_o^2\nonumber\]

\[KE_{2~after}=\frac{1}{2}I_2\omega_2^2=\frac{1}{2}\left[\frac{1}{2}m_2R_2^2\right]\left(\frac{R_1}{R_2}\right)^2\left(\frac{m_1}{m_1+m_2}\right)^2\omega_o^2=\frac{1}{2}\left(\frac{1}{2}mR^2\right)\left(2\right)^2\left(\frac{4m}{4m+m}\right)^2\omega_o^2=\frac{16}{25}mR^2\omega_o^2\nonumber\]

\[KE_{total~after}=KE_{1~after}+KE_{2~after}=\frac{16}{5}mR^2\omega_o^2\nonumber\]

The "before" kinetic energy is:

\[KE_{total~before}=\frac{1}{2}\left(\frac{1}{2}m_1R_1^2\right)\omega_o^2=\frac{1}{4}\left(4m\right)\left(2R\right)^2\omega_o^2=4mR^2\omega_o^2\nonumber\]

The thermal energy created is therefore:

\[\Delta E_{thermal}=KE_{total~before}-KE_{total~after}=\frac{4}{5}mR^2\omega_o^2\nonumber\]

And as a fraction of the total initial kinetic energy this is:

\[\dfrac{\Delta E_{thermal}}{KE_{total~before}}=\dfrac{\frac{4}{5}}{4}=\frac{1}{5}\nonumber\]

So 20% of the initial kinetic energy becomes thermal.

Problem 6.2

The center of a uniform solid disk is threaded onto an axle at the end of a thin uniform rod. The rod and the disk have equal masses, and the radius of the disk is one-third the length of the rod. The rod is attached to a fixed pivot point at its other end, around which it is free to rotate. With the rod and disk both starting from rest, a force of constant magnitude is exerted tangent to the edge of the disk at the point farthest from the pivot for a short time. There is no gravity present.

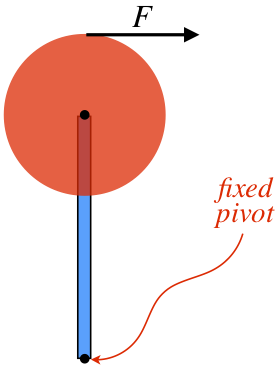
After the applied force is removed, the disk and rod are spinning freely. Of the full system's angular momentum, determine what fraction of it comes exclusively from the motion of the rod.

Solution

From the analysis, the total angular momentum of the system in terms of the mass of the rod and its rotational speed is:

\[L_{system}=16mR^2\omega_1\nonumber\]

The angular momentum of the rod only is its moment of inertia about the fixed pivot multiplied by its rotational speed:

\[L_{rod} = I_{rod}\omega_1=\frac{1}{3}m\left(3R\right)^2=3mR^2\omega_1\]

The fraction of the system's angular momentum about the pivot that comes from just the rod's motion is therefore \(\frac{3}{16}\).

Problem 6.3

Consider this position-dependent force:

\[\overrightarrow F\left(x,y\right) = \lambda \left[x\;\widehat i + y\;\widehat j \right] \nonumber \]

A rock is tied to a string whose other end is held fixed at the origin, and is then set into circular motion in the \(x–y\) plane (there is no gravity present). While the rock is moving at a constant speed in a circle, the force described above is turned on.  The string later breaks and the rock eventually crosses the \(x\)-axis.

The string has a length of \(0.50m\), the rock has a mass of \(0.30kg\), and rock revolves around at a speed of \(4.0\frac{m}{s}\). After the string breaks, when the rock crosses the \(x\)-axis at \(x=2.5m\), its does so moving at an angle of \(7.9^o\) with that axis. Find the work done by the force \(\vec F\) from the point when the string breaks to the point where the rock crosses the \(x\)-axis.

Solution

We can determine the final speed of the rock using the result from the analysis:

\[v_f=\dfrac{v_oR}{x\sin\theta}=\dfrac{\left(4.0\frac{m}{s}\right)\left(0.50m\right)}{\left(2.5m\right)\sin 7.9^o}=5.82\frac{m}{s}\nonumber\]

With the final speed of the rock, we can compute its kinetic energy, and the amount of kinetic energy gained from the point when the string breaks equals the work done by the only force acting, \(\vec F\):

\[W=\Delta KE = \frac{1}{2}m\left[v_f^2-v_o^2\right]=\frac{1}{2}\left(0.30kg\right)\left[\left(5.82\frac{m}{s}\right)^2-\left(4.0\frac{m}{s}\right)^2\right]=2.68J\nonumber\]

Problem 6.4

A large uniform-density disk of radius \(R\) rotates in a horizontal plane around a frictionless axle with a rotational speed \(\omega\). This disk includes a vertical post located a distance half its radius from its axle, and onto this axle is placed (very suddenly) a second disk with half the radius of the larger disk. The second disk is made of the same uniform material as the larger disk, and has the same thickness.

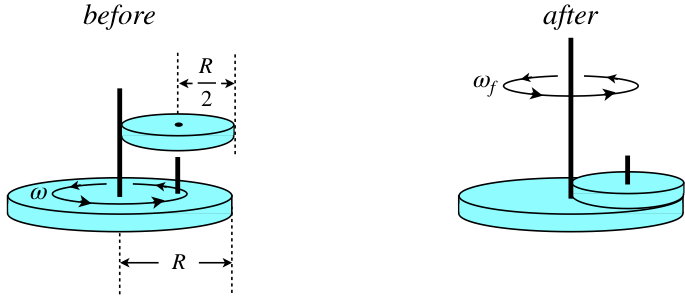
Kinetic friction between the disks acts until the smaller disk no longer spins on the lower disk, and instead turns with the larger disk as if their surfaces were glued. The work done by this kinetic friction equals the increase in the thermal energy of the two disks. Find this increase in thermal energy for the system as a fraction of its initial kinetic energy.

Solution

In the analysis we found the final rotational velocity in terms of the initial velocity for the "friction" case:

\[\frac{\omega_f}{\omega}=\frac{16}{19}\nonumber\]

The angular momentum of the system remains conserved, and the kinetic energy can be written as:

\[KE_{rot}=\frac{1}{2}I\omega^2=\frac{1}{2}\left(I\omega\right)\omega=\frac{1}{2}L\omega\nonumber\]

Using this expression, we can compute the ratio of the kinetic energy after to the kinetic energy before:

\[\dfrac{KE_{after}}{KE_{before}}=\dfrac{\frac{1}{2}L\omega_f}{\frac{1}{2}L\omega}=\dfrac{\omega_f}{\omega}=\frac{16}{19}\nonumber\]

The remaining fraction of the energy is what goes to thermal, so:

\[\dfrac{\Delta E_{thermal}}{KE_{before}}=\frac{3}{19}\nonumber\]