1.35: Einstein Relativity
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the 19th century it was discovered that the Maxwell Equations describing electric and magnetic fields, a grand synthesis of the results of many different experiments, unlike Newton's laws of motion, are not consistent with Galilean relativity. A priori, the solution was not clear. One possible reason for this inconsistency, taken seriously at the time, was that the principle of relativity is wrong; i.e., there actually is an absolute rest frame, and our motion could be detected with respect to it with the appropriate experiment. Indeed, there was a significant experimental program to detect our motion with respect to absolute rest defined by a medium called "the ether."
Another possibility, is that while the principle of relativity holds, its specific implementation as Galilean relativity does not. As you know, because you have studied special relativity, this is indeed the correct solution to the puzzle of the Maxwell Equations lack of invariance under a Galilean transformation.
It turns out that the "Galilean Boost" can be generalized to a "Lorentz Boost" that is also consistent with the principle of relativity. The primed and unprimed coordinate systems constructed as before, under a Lorentz boost are related as:
t′=γ(t−vx/c2)x′=γ(x−vt),y′=y, andz′=z
where γ≡1/√1−v2/c2. In the limit that c→∞ this reduces to the Galilean boost. As can be easily shown (see the homework problem) the reverse transformation is the same rule with v→−v. Most importantly, the Maxwell equations are invariant under this transformation.
One of the more spectacular consequences of the Maxwell Equations is that one of their solutions is waves traveling at the speed of light. If the Maxwell equations are correct in all inertial frames, then this implies that these waves will be moving at the speed of light in all inertial frames. To your Galilean intuition this is quite startling as it violates the simple rule for addition of velocities you derived in the previous chapter.
The result can be easily demonstrated from the Lorentz transformation above. Here we sketch out the process, and you can fill in the details by performing the exercise that follows. Imagine a particle traveling at the speed of light. Let's parameterize its path through spacetime with the independent variable λ so that t=λ and x(λ)=cλ. Then we have (by direct substitution into the Lorentz transformation) that t′=(γ/c)(c−v)λ and x′=γ(c−v)λ. The speed of this particle in the primed frame is
dx′dt′=dx′dλdλdt′=dx′dλ(dt′dλ)−1=c.
Thus we see the Lorentz transformation tells us that a particle traveling at speed c in one frame will be traveling at speed c in another. This result is consistent with our claim that the Maxwell equations are invariant under the Lorentz transformation, since a consequence of the Maxwell Equations is that electromagnetic waves travel at speed c.
Box 1.35.1
Exercise: 4.1.1: Fill in the steps in the above derivation.
Unlike rotational coordinate transformations that preserve spatial distances between pairs of points, a Lorentz transformation does not. The spatial separation between (x,t) and (x+dx,t) is dx. The spatial separation between these points in the prime frame is γdx, as one can see from the transformation rule. How can length depend on reference frame? Key to resolving this apparent paradox is the fact that in the primed frame the two events are not simultaneous. We won't sort out these apparent paradoxes here.
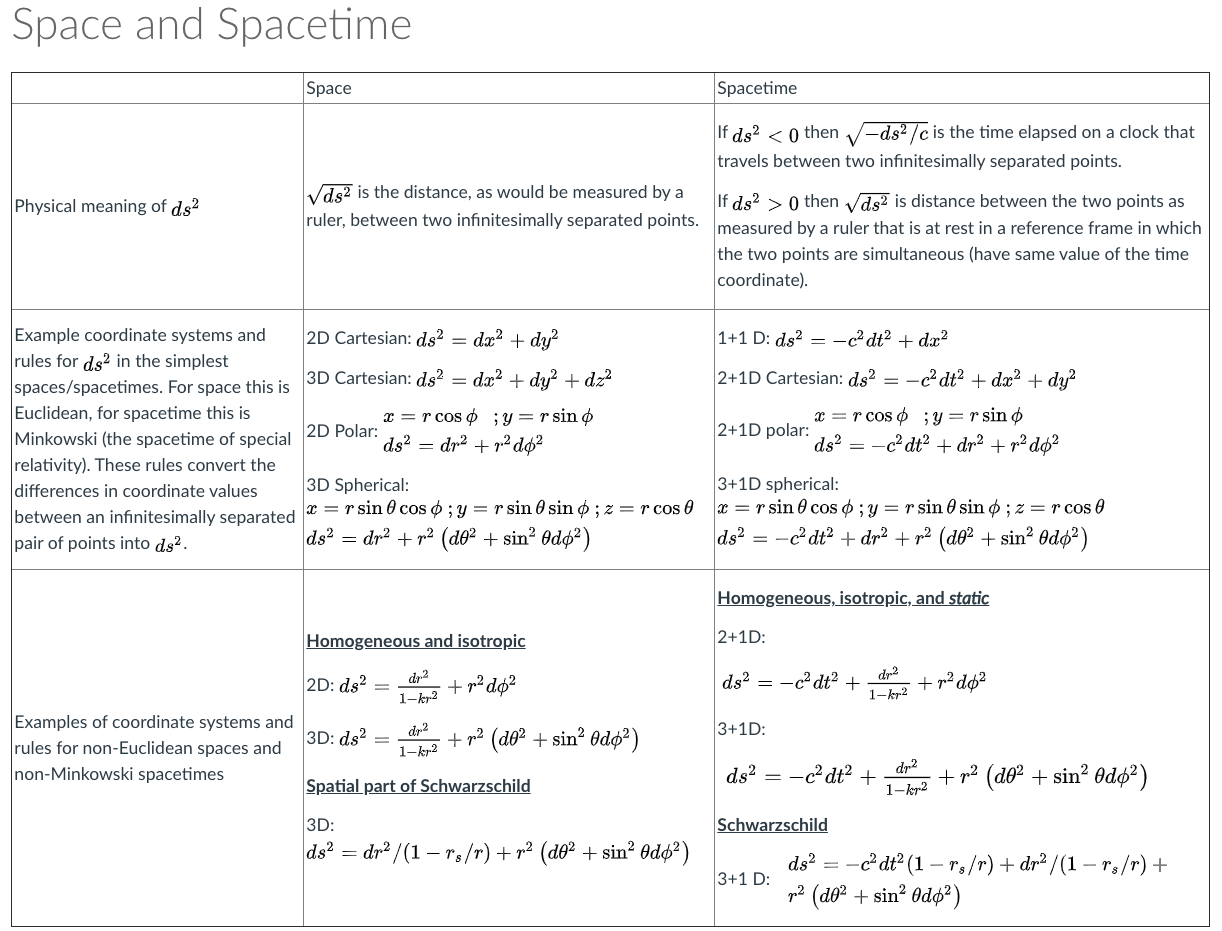
We will, however, introduce a quantity that, unlike spatial length, is invariant under Lorentz transformations. For Cartesian spatial coordinates, the square of the invariant distance between event (t,x,y,z) and event (t+dt,x+dx,y+dy,z+dz) is given by
ds2=−c2dt2+dx2+dy2+dz2.
This quantity has the following two-part physical interpretation:
- For ds2>0, √ds2 is the length of a ruler that connects the two events and is at rest in the frame in which the two events are simultaneous.
- For ds2<0, √−ds2/c2 is the time elapsed on a clock that moves between the two events with no acceleration.
Why is this quantity invariant under boosts? That's a deep question, and I'm not sure we have the fullest possible answer yet sorted out. We do know that the Maxwell equations are a synthesis from experiments, their form is invariant under a Lorentz transformation, and the Lorentz transformation preserves the invariant distance.
Let's show that the invariant distance is indeed invariant under a Lorentz transformation. For specificity, take it to be the transformation appropriate for a boost in the +x direction with speed v. For simplicity, we will take your two coordinate systems to be coincident at their origins (i.e. t=x=y=z=0 is the same point as t′=x′=y′=z′=0 ), use the origin as one point, let's call it point A, and t=dt,x=dx,y=dy,z=dz as the other, let's call it point B. The invariant distance between these two points is
ds2=−c2dt2+dx2+dy2+dz2.
In the primed frame point A is the origin (by construction) and point B is labeled with t′=dt′,x′=dx′,y′=dy′,z′=dz′.
Thus the invariant distance in the primed frame is
(ds′)2=−c2(dt′)2+(dx′)2+(dy′)2+(dz′)2. We want to show that (ds′)2=ds2.
So we need to know how dt′ and dx′ etc., are related to dt, dx, etc. Since the boost is in the x direction by speed v we have, from Equation ???:
dt′=γ(dt−vdx/c2)dx′=γ(dx−vdt),dy′=dy, anddz′=dz.
The easier direction to go here is to start with
(ds′)2=−c2(dt′)2+(dx′)2+(dy′)2+(dz′)2 and work our way toward showing that this equals −c2dt2+dx2+dy2+dz2 so let's do that. By completing the exercise below you will see that these are indeed equivalent, and thereby show that the invariant distance between two infinitesimally separated points in spacetime is invariant under a Lorentz transformation.
Box 1.35.2
Exercise 4.2.1:
Show that (ds′)2=−c2(dt′)2+(dx′)2+(dy′)2+(dz′)2 is the same as −c2dt2+dx2+dy2+dz2 if the two coordinate systems are related by a Lorentz transformation; i.e., complete the demonstration as set up in the text immediately above. To give you a little less writing to do, feel free to drop the y and z coordinates (and their primed versions) since their transformation is trivial. Keep in mind that 1/γ2=1−v2/c2.
Rather than the Lorentz transformation itself, the key thing to take away from this chapter is the definition of the invariant distance. We will be using it for the rest of the course, generalized to spacetimes with "curvature." Before doing so, we give some exercises here in which you get to make use of the invariant distance to solve problems in the more familiar context of a flat spacetime, the so-called Minkowski space you are familiar with from special relativity. A Minkowski space is simply a spacetime that can be labeled with t,x,y,z such that the invariant distance is given by Equation ???.
In Minkowski space, as one of the homework problems asks you to show, a finite (as opposed to infinitesmial) version of the invariant distance equation is also true:
(Δs)2=−c2(Δt)2+(Δx)2+(Δy)2+(Δz)2
for trajectories that are straight lines, with Δs≡∫dλdsdλ also invariant under Lorentz transformations.
To demonstrate some of the utility of the invariant distance equation let's use it to derive the phenomenon of time dilation. Specifically, let's calculate the time that elapses on a clock traveling in a straight line at speed v from x1,t1 to x2,t2. We will find that it is not t2−t1.
First, let's draw the trajectory of the clock on two spacetime diagrams: one with a coordinate system in which the clock is moving with speed v and the other with a coordinate system that has the clock at rest.
The time that elapses on the clock as it travels between these two points will be t′2−t′1. We know this because we assume it is a good clock and the primed coordinate system has been constructed so that this is the case for clocks at rest in the primed coordinate system. (We also assume the same about the construction of the unprimed coordinate system, that a clock at rest there, will show a time elapsed of t2−t1 as it travels, without spatial translation, from a spacetime point with time coordinate t1 to a spacetime point with time coordinate t2).
For the first coordinate system we have an invariant distance between points 1 and 2:
(Δs)2=−c2(t2−t1)2+(x2−x1)2=−c2(Δt)2+(Δx)2.
For the prime system we have an invariant distance between points 1 and 2:
(Δs′)2=−c2(t′2−t′1)2.
Now we set them equal and solve for t′2−t′1:
−c2(t′2−t′1)2=−c2(Δt)2+(Δx)2(t′2−t′1)2=(Δt)2−(Δx)2c2notethat,(Δx)2(Δt)2=v2(t′2−t′1)2=(Δt)2(1−v2c2)t′2−t′1=γ−1Δt
So we see that the time elapsed on the clock is not Δt=t2−t1 but instead Δt/γ.
Note that we could also have just calculated (Δs)2 in the unprimed frame and used our physical interpretation of √−(Δs)2/c2 (for (Δs)2<0 ) as the time that elapses on a clock traveling from point 1 to point 2.
Box 1.35.3
Exercise 4.3.1: In the above derivation we identified Δx/Δt as the speed of the clock v. Why is this justified?
Summary and Discussion
In our study of spatial geometry we came to view coordinates as mere labelings of points in a space, with no physical significance on their own. Physical significance came through a rule that related infinitesimal differences in the coordinate values of a pair of points to an infinitesimal distance, ds. Now we have extended space to spacetime with the introduction of a temporal coordinate, that so far we have always called t. Once again we label all the points in a spacetime with coordinates that have no physical significance on their own. Physical meaning comes through a rule relating infinitesimal differences in the coordinate values of a pair of points to something observable, although in this case the rule is a bit more complicated.
You might ask why the rule is more complicated; why is it the way it is? To which one could answer, "we do not know; we just work here!" To expand on this, we do not know why the rule is as it is, but we have discovered through experiments, and abstraction from these experiments, that this rule works. Through the exercises and homework problems you can see how this rule naturally incorporates the phenomenon of time dilation. You could also work out for yourself how it incorporates the phenomenon of Lorentz contraction. The rule basically encapsulates what we have discovered about the local structure of spacetime.
The rule is telling us about the local structure of spacetime in the sense that it is telling us about time spans and lengths associated with points that are only separated by infinitesimal amounts. This local aspect is preserved as we move on, in subsequent chapters, to study the global structure. Thus the infinitesimal invariant distance is an important concept in our study of the expansion of the universe.
In the table below we summarize the physical meaning of ds2 and the rules relating coordinate separations to observables for a variety of spaces/spacetimes and coordinate systems. So far the spacetimes we have introduced have been static; not evolving in time. In the next chapter we will introduce a dynamic spacetime, a 1+1-dimensional analog of the expanding spacetime we appear to inhabit, and then begin to study the observable consequences of these changes over time.
HOMEWORK Problems
Problem 1.35.1
Show, by solving for x and t that the inverse Lorentz transformation is the same as the forward transformation but with v→−v. Explain what this has to do with the principle of relativity.
Problem 1.35.2
Show that for straight paths in spacetime, that (Δs)2=−c2(Δt)2+(Δx)2 follows from ds2=−c2dt2+dx2. Hint: all straight paths in spacetime (at least the flat spacetime of special relativity we are studying now) can be parametrized via: t−t0=λ,x=x0+vλ.
Problem 1.35.3
Events A and B occur 10 meters and 100 ns apart in time in frame 1. If they occur 95 ns apart in frame 2, what must their spatial separation be in frame 2?
Problem 1.35.4
An astronaut leaves Earth and then returns to find their twin is much older. Assume one twin stays at rest on the Earth while the other departs at speed v and then turns around and comes back to their twin once again at speed v. Assume the time elapsed for the stay-at-home twin, between departure and return, is t2−t1. How much time elapses for the astronaut twin between departure and return? Draw a spacetime diagram in a frame that has the stay-at-home twin at a fixed location and make use of the invariant distance.