3.4: Particle Model of Thermal Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Overview
In the previous section we modeled the macroscopic definition of bond energy from Chapter 1 with the microscopic perspective of neutral subatomic particles interacting with a pair-wise potential. In this section we will attempt to make the same connection for thermal energy. In Chapter 1 for pure substances in the temperature range where the Three-Phase Model is valid we said that the total energy of a system is given by:
Etot=Eb+Eth
In the microscopic description of particles interacting with the Lennard-Jones potential the total energy of a system is:
Etot=PEtot+KEtot
The subscript "tot" refers to the sum of kinetic and potential energies over all particles. Although, we will focus on just two particles for now, for generality, we add the "tot" subscript so the equations can be applied to many-particles systems, as well. In the previous section we said that macroscopic bond energy can be modeled as the sum of pair-wise potential energies between all pairs at their equilibrium configurations (at zero temperature). Your instinct might tell you that thermal energy should be represented in terms of the sum over all the kinetic energies of the particles. But careful! If we add some energy to the two-particle system without breaking the bond, the bond energy does not change, so only thermal energy changes. And as we discussed in Section 3.2, when energy is added to the system the particles begin to vibrate about equilibrium. As energy is added to the system increasing thermal energy only, the range of fluctuations increasing, which increases both the average potential and kinetic energy, as can be viewed on the figure below.
Figure 3.5.1: Total Energy in a two-particle system.
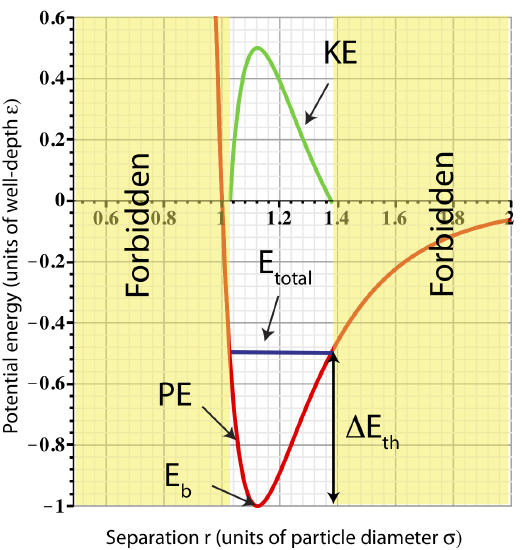
Thus, thermal energy is related to potential energy, as well as kinetic. When energy is added, it is not possible to increase kinetic energy without increasing potential energy. As in the spring-mass system when you add potential energy by stretching the spring further, you will also increase the kinetic energy as the spring will oscillate faster on average. In Section 2.6 we discussed that averaged over time the kinetic and potential energies are the same for a spring-mass system, and as a result half of the total energy. Since the Lennard-Jones potential mimics the spring-mass potential at least for small oscillations, we will assume that this interaction when averaged over time will also result in KEavg=PEavg. When energy is added without breaking bonds all the energy goes into thermal energy which is equally split between kinetic and potential energy:
KEtot=Eth2
The potential energy that contributes to the other half of thermal energy has to do with the random vibrations, but there is also the part of potential energy that is equal to bond energy at zero temperature before energy was added:
PEtot=Eth2+Eb
To check the validity of these equations add them together to get:
KEtot+PEtot=Eth+Eb
which is precisely the two definitions of total energy given in Equations ??? and ???, making the connection between the microscopic and the macroscopic descriptions of total energy.
We saw here that as thermal energy increases the particles start to vibrate about their equilibrium. Thus, thermal energy has to do with the random fluctuations of the particles, while bond energy has to do with their equilibrium configurations. We also discussed the idea of added energy being split evenly between kinetic and potential energies, which will bring us to the idea of Equipartition of Energy below.
Particle Model of Thermal Energy
In the Particle Model of Thermal Energy we describe thermal energy of a macroscopic solid of liquid in terms of random fluctuations of subatomic particles which vibrate in the three spacial dimensions. Since most vibrating systems can be described by a spring like potential, we will model these oscillating particles as a masses held in place by three perpendicular springs, one for each independent spacial dimension, as depicted in the figure below.
Figure 3.5.1: Model of thermal energy with particles attached to springs.
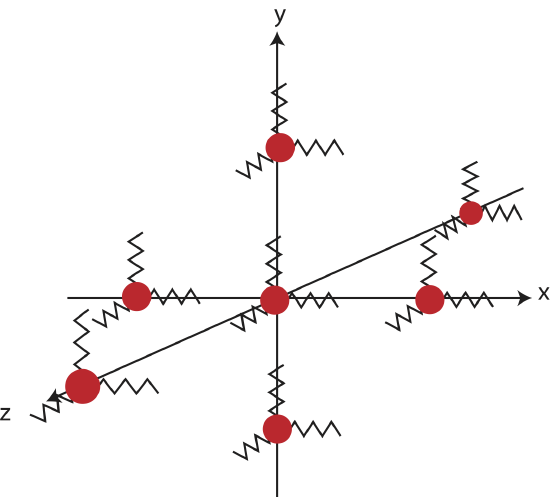
In order to make sense of how thermal energy can be formulated from these random fluctuations, we would like to know how many ways does each of these particles can “have energy” and how is the total energy distributed among these different "ways"? To answer this within the constraints of our model, we start with the fact that a spring-mass system has a kinetic and a potential energy. Because of the randomness or disorder of thermal motions of the microscopic spring-masses in all three spacial directions, it is plausible that on average, each spring would have the same average KE and PE, as would any other spring. The potential and kinetic energies that are associated with those oscillations can each be divided into three independent terms, each one corresponding to one of the three independent spatial dimensions. Therefore, each particle in a liquid or solid has at least these six independent ways it can "have energy".
The important point to remember here, is that regardless of the actual kind of chemical bonding (types of bonds and the geometrical configuration of the bonds) the thermal energy due to the oscillation of the atoms or molecules (treated as rigid particles) is modeled as if they are connected by three independent springs, corresponding to the three independent spatial dimensions in a 3-D universe.
Unbound atoms in the gas phase have other ways to have energy, they can move around freely in space. If the gas is made up of molecules, the individual molecules can also rotate and vibrate. There is a name, or label, for “way to have energy", which we call a mode, also sometimes referred to as a degree of freedom.
Equipartition of Energy
When we discussed a two-particle system, we argued that it is reasonable to assume that half of the thermal energy goes to kinetic and the other half to potential when averaged over time. From the particle model perspective when a macroscopic system reaches thermal equilibrium the energy associated with random fluctuations (the motions of particles about their equilibrium positions in a solid or liquid or their random motions when in the gas phase) is uniformly distributed throughout the entire sample. That is, there will be about as much energy associated with the random energies of a small piece of the sample as in any other same size small piece. This is known as Equipartition of Energy. It is similar to what we would say about temperature, if we wait for a sufficiently long time, the temperature will become uniform throughout the sample. There would seem to be a direct connection between temperature and the disordered random motion associated with thermal energy.
Using tools of statistical mechanics (which is beyond the scope of this course) it can be shown that each type of energy that a substance can have, or each mode, has this amount of thermal energy:
Ethermal(per mode)=12kBT
where kB=1.38×10−23J/K is the Boltzmann constant and T is temperature. This expression provides a connection between a macroscopic concept of temperature and a microscopic idea of a mode. In words the above equation means that temperature is a measure of the average energy in an active mode when the sample is in thermal equilibrium. To calculate the total thermal energy, we need to multiple the 12kBT factor for the thermal energy per mode by the total number of modes in our sample. The total number of modes is the total number of particles N times the number of modes per particle. Thus, total thermal energy can be written as:
Ethermal=(# modes per particle)×N×12kBT
Our next task to to count the number of modes per particle for different types of substances.
Counting Modes
When we asked how many ways does each spring in a solid can have energy, the answer was two, one kinetic and one potential. We will refer to these modes as the vibrational kinetic energy, KEvib, and vibrational potential energy, PEvib modes. To answer how many ways does each particle in a solid have to have energy, we saw that there are three springs and two modes per spring, so a solid must be six number of modes, 3 KEvib modes and 3 PEvib. Equipartition of Energy tells us that each one of these modes will have the same amount of energy of 12kBT at thermal equilibrium. One mole of a solid will have 6NA number of modes, resulting in a total thermal energy of:
Ethermal=3NAkBT
How many modes do different gases have? In a simple monatomic gas, composed of single atoms, such as He or Ne gases, aka Noble gases, the atoms are no longer interacting with a pair-wise potential since their average separations are r∼10σ. Therefore, the atoms cannot be modeled with springs since they are not vibrating around some equilibrium. Rather the atoms are moving around freely in three-dimensions. We refer to this type of motion as translational kinetic energy, KEtrans. Since there are three dimensions, each atom in a monatomic gas will have 3 modes. We can find the average speed of a gas particle by considering that each of the three KEtrans modes has 12kBT of thermal energy. Thus:
KEavg=12mv2avg=32kBT
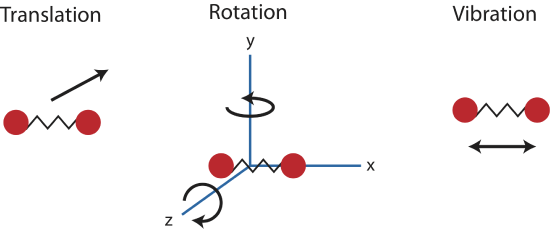
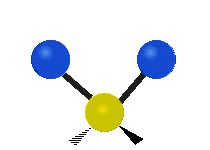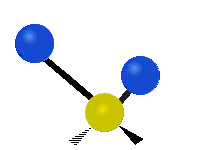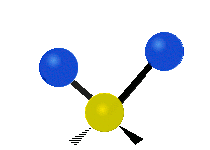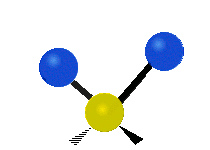
In a diatomic gas, composed of two-atom molecules, such as H2 or O2, there are still no inter-molecular (between molecules) interactions, but there are now intra-molecular (between the atoms within a molecule) interactions to consider. We can model the bond between the two atoms in a molecule as a spring, allowing the two atoms to vibrate relative to each other. Thus, each molecule will have one vibrational kinetic and potential energy mode. In addition, as for the monatomic gas, the molecule as a whole is free to move in space, since it is not interacting with other molecules. Thus each molecule has 3 translational kinetic energy modes. Another way this molecule can have kinetic energy is through rotations. The figure below depicts all the possible rotational modes of a diatomic molecule. The energy associate with rotations is known as rotational kinetic energy, KErot. For a diatomic molecule only two rotational modes are energetically allowed (for quantum mechanical reasons we will not address here). As shown in the figure these are rotations about the y- and z- axes. One way to think about this is that only rotations that change the orientation of the molecule or are not symmetric, are energetically allowed. Thus, since rotating the molecule about the x- axis is symmetric, this rotation is not allowed. For a diatomic gas we have found a total of 7 modes: 3 KEtrans, 2 KErot, 1 KEvib, and 1 PEvib.
Figure 3.5.2: Modes in a diatomic molecule.
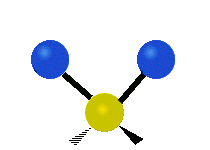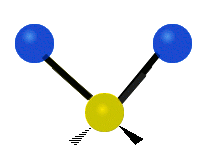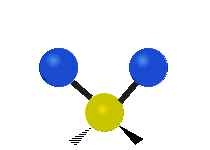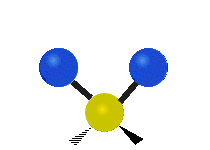
Generally, a polyatomic gas is composed of molecules having N number of atoms. A molecule is linear, when all atoms are arranged in a straight line, such as all diatomic molecules. Other examples of linear molecules are CO2 and C2H2. All linear molecules have 3 KEtrans modes and 2 KErot. Non-linear molecules, such as H2O, are not symmetric can rotate around all 3 axes, thus have 3 KErot modes. Counting the number of vibrational modes directly can get tricky. Below is a depiction of all the possible vibrational modes in a non-linear triatomic molecule.
Figure 3.5.3: Possible vibrational modes in a non-linear triatomic molecule.
| Symmetric Stretching | Asymmetric Stretching | Scissoring (bending) |
|---|---|---|
 |
 |
 |
However, without thinking about the geometry of all the possible vibrations, we can count the number of vibrational modes indirectly. If we treat each atom in a polyatomic molecule independently, we conclude that the molecule has 3N kinetic energy modes, 3 for each atoms. We know that a non-linear molecule will have 3 KEtrans and 3 KErot. To add up to 3N total kinetic energy modes, 3N=3+3+(KEvib), we find that there must be (3N-6) KEvib modes. For each kinetic vibrational mode there has to be a potential vibrational mode, so there are also 3N-6 PEvib modes. Thus, the total number of possible modes in a non-linear polyatomic molecule is:
total number of modes=3(KEtrans)+3(KErot)+(3N−6)(KEvib)+(3N−6)(PEvib)=6N−6
Similar analysis can be done for a non-linear molecules. A summary of the number of modes for all the types of substances is shown in the table below.
Table 3.5.1: Number of Modes for Different Substances in 3D.
| Type of Substance | Translational Modes | Rotational Modes | Vibrational Modes | Total Modes per particle |
|
Solid |
0 |
0 |
6 |
6
|
| Monatomic Gas | 3 | 0 | 0 | 3 |
|
Linear Polyatomic Gas (N atoms) |
3 |
2 |
6N-10 |
6N-5 |
|
Non-linear Polyatomic Gas (N atoms) |
3 |
3 |
6N-12 |
6N-6 |
Sometimes, however, some of the modes do not “get excited” due to the quantization of energy levels. At low temperatures, the quantum splitting between energy levels is larger than thermal energy, and the mode cannot be activated. When this happens, we say that mode is frozen out. Frozen modes cannot share thermal energy among other modes. Active modes are the only ones that share the thermal energy equally among themselves. Rotational modes typically have lower energy than vibrational modes. Thus, vibrational modes are frozen out for typical temperatures, but rotational modes can also become inactive when the temperature is low enough. Translational modes are always active, as long as the temperature is above zero Kelvin.
Example 3.4.1
1) You perform various experiments to determine properties of an unknown substance. In one experiment, you place 10 moles of a solid and 12 moles of the unknown substance in separate insulated and sealed containers. You find that when you add the same amount of energy to each container, you measure the same temperature change. Assume there are no phase changes for either substance. Determine whether the unknown substance is a solid, monatomic gas, diatomic gas with frozen vibrational modes, or a diamotic gas with active vibrational modes.
2) In another experiment you combine 2 moles of a solid with 3 moles of a diatomic gas with vibrational modes frozen in an insulated contained. The two substances are initially at different temperatures. As the two substances reach thermal equilibrium, which one will have a larger magnitude of a temperature change?
- Solution
-
1) In the Particle Model of Thermal Energy the change in thermal energy is given as:
ΔEthermal=(# modes per particle)×N×12kBΔT
Since ΔEthermal is the same for the same ΔT for both substances, the total number of modes must be the same for both substances. The total number modes is the number of particles times the number of modes per particle, so for the solid we get:
total # modes=10NA×6=60NA
For the unknown substance:
total # modes=60NA=12NA( # modes per particle)
resulting in (# modes per particle) = 5, which is true for a diatomic gas with frozen vibrational modes.
2) Since the two substances are a closed system, ΔEthermal gained by one substance must equal be ΔEthermal lost by the other:
(total # modes of solid )|ΔTsolid|=(total # modes of gas)|ΔTgas|
From equation above, the substance with less total # of modes will have a larger temperature change. The solid has 2NA×6=12NA total number of modes, and the diatomic gas with vibrational modes frozen out has 3NA×5=15NA total number of modes. Thus, the solid will have a larger temperature change.
Heat Capacity at Constant Volume
Let us now make the connection between the definition of macroscopic thermal energy from Chapter 1 and the microscopic description presented here. Specifically, we would like to develop an understanding of heat capacity from Chapter 1 in terms of microscopic parameters. But we need to be careful that we are actually comparing the same things. We know that if a force acts through a distance, work will be done by one physical object on another. When we make a heat capacity measurement, we do not want the sample doing work on the atmosphere or the container it is in. Therefore, we specify that the sample be kept at constant volume during the heat capacity measurement. The important point here is that we have a way to directly measure the change in the thermal energy by measuring the heat capacity of a sample at constant volume, ensuring all the heat we put into the sample goes to changing its thermal energy and not doing some work by expanding the container or pushing against the air in the room. From the Energy-Interaction Model when no work is being done and only temperature is changing we have ΔEtot=ΔEth=Q. When the change in thermal energy is due solely to the addition or removal of energy as heat, the constant volume heat capacity, designated with subscript "v", CV, is given by the rate of change of thermal energy with respect to temperature. This is precisely how we defined thermal energy in Equation 1.2.6 in Chapter 1:
except now we add the "V" subscript for accuracy. The expression above is the macroscopic definition of thermal energy at constant volume. Let us compare the above equation with Equation 3.4.7 described in the Particle Model of Thermal Energy. Setting the two equations equal to each other, using the gas constant R=NAkB=8.314JKmol, and solving for molar heat capacity cv,mol (CV=cv,mol for one mole or NA number of particles), we get:
cv,mol=R2(# modes per particle)
We have simple expression above that connects the idea of heat capacity that can be experimentally measured in a lab using macroscopic substances with the microscopic idea of each particle in a substance having an energy mode. We will check the validity of this model next, when we look at some data patterns.
Example 3.4.1
UC Davis scientists construct the following one-dimensional solid structure from their newly discovered atoms, Aggieum (Ai) and Cyclerium (Cy):

The total number of atoms is 4NA. The double lines represent strong Ai-Cy bonds, where the single lines are weaker AiCy-AiCy bonds. Each particle is free to move in one-dimension only.
a) Calculate the heat capacity Cv for the substance in the diagram.
b) You add enough energy to break all weaker bonds. The resulting gas particles are free to move in three-dimensions. Calculate the heat capacity Cv for this substance assuming all modes are active.
c) You add some more energy, and notice that at T=500K all of the stronger bonds are broken as well. If the mass of Ai is nine times the mass of Cy, calculate the ratio of their speeds at T=500K.
d) You take two moles of the substance in part a) and one mole of the substance in part b) and place them together in an insulated container. Compare the magnitudes of the changes in thermal energy of the two substances as they come to thermal equilibrium. Assume there is no change in bond energy in the interval you are analyzing.
- Solution
-
a) Since each atom in this solid can only move in one-dimension, there are 2 modes per atom, one PE and one KE. Heat capacity:
Cv=ncv,mol=4×(# modes per particle)×R2=33.26J/K
b) After the weak bonds are broken the AiCy molecules are no longer interacting, so we have a diatomic gas. If all modes are active, there are 7 modes per molecule. Since there are 4NA total atoms, there will be 2NA AiCy molecules. Heat capacity:
Cv=ncv,mol=2×7×R2=58.2J/K
c) Ai and Cy atoms are at the same temperature, thus they’ll have the same KE=32kBT=12mv2. Setting the two kinetic energies equal to each other:
12mAiv2Ai=12mCyv2Cy
v2Cyv2Ai=mAimCy=9
vCyvAi=3
Thus, Cy atoms are on average moving three times faster than Ai atoms.
d) Only the idea of energy conservation is needed to answer this question. They are in an insulated container:
ΔEth,a+ΔEth,b=0
Thus, both will have the same magnitude of change in thermal energy.
Data Patterns
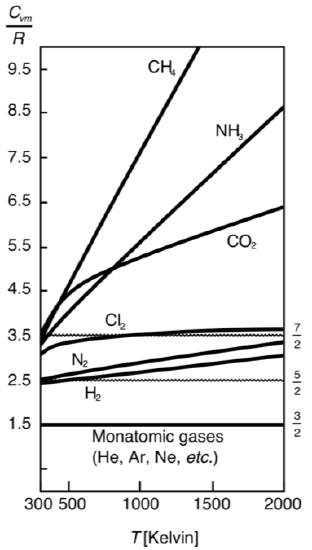
The figure below shows the constant volume molar heat capacity, scaled with gas constant, for several gases from room temperature up to several thousand kelvin. Since cv,mol/R=(# modes per particle)/2, the plot is showing us how the number of modes per particle changes with temperature. The monatomic gases have the lowest molar constant volume heat capacity of 32R, and the values are independent of temperature. Diatomic gases seem to have higher values starting at about 52R, while polyatomic gases have significantly larger values, but also a much more pronounced temperature dependence. This data tells us that not all modes are active at all temperature. As we previously discussed at lower temperature some modes get frozen out when there is not enough energy to overcome the quantum energy gap to excite a particular mode. For example, we see that around room temperature diatomic molecules have 5 modes, instead of the possible 7 modes, implying that the two vibrational modes are inactive. This data shows an average over one mole of particles, this is why the number of modes changes smoothly (rather than by integer count) as modes become activated in an increasing number of particles as temperature increases.
Figure 3.5.4: Heat Capacity as a function for temperature for various gases.
The table below shows heat capacity patterns that are seen in different gases. Each type of gas, e.g., monatomic, has similar values of specific heats, and the values are ordered from smaller to larger as we go from monatomic to diatomic to triatomic, as implied by Equation ???. We will analyze in the next chapter why the specific heats of gases measured at constant pressure are greater than at constant volume, as well as the similar difference between Cmp and Cmv for all gases.
| gas | Cmp | Cmv | CmvR | Cmp−Cmv | (Cmp−Cmv)R |
| Monatomic | |||||
| He | 20.79 | 12.52 | 1.51 | 8.27 | 0.99 |
| Ne | 20.79 | 12.68 | 1.52 | 8.11 | 0.98 |
| Ar | 20.79 | 12.45 | 1.50 | 8.34 | 1.00 |
| Li | 20.79 | 12.45 | 1.50 | 8.34 | 1.00 |
| Xi | 20.79 | 12.52 | 1.51 | 8.27 | 0.99 |
| Diatomic | |||||
| N2 | 29.12 | 20.80 | 2.50 | 8.32 | 1.00 |
| H2 | 28.82 | 20.44 | 2.46 | 8.38 | 1.01 |
| O2 | 29.37 | 20.98 | 2.52 | 8.39 | 1.01 |
| CO | 29.04 | 20.74 | 2.49 | 8.30 | 1.00 |
| Triatomic | |||||
| CO2 | 36.62 | 28.17 | 3.39 | 8.45 | 1.02 |
| N2O | 36.90 | 28.39 | 3.41 | 8.51 | 1.02 |
| H2S | 36.12 | 27.36 | 3.29 | 8.76 | 1.05 |


