9.2: Particle Model of Light

Photons

In a previous chapter, we found that light behaves like a wave in a variety of circumstances, such as the interference pattern that light exhibits when it is sent through a double-slit setup. Prior to the two-slit experiments, physicists had been uncertain about the nature of light. Prominent physicists, including Isaac Newton, strongly believed that light was more like a particle than a wave, but the two-slit interference patterns of light could be understood so well with the wave model that for a while the subject was laid to rest.

However, in the early 20^th century, several circumstances involving light brought the particle model back into consideration. Eventually, enough evidence accumulated to conclude that light behaves in ways that can be explained by a particle model, but cannot be explained by a wave model. Presently, we must hold in our minds both the wave model of light and the particle model of light. In some circumstances, the behavior follows the wave model, but in other circumstances, it follows the particle model.

The Photoelectric Effect

One of the first experiments which is exhibited strong experimental evidence of light behaving like a particle was the photoelectric effect, which first led Albert Einstein to develop the particle model of light. In the photoelectric effect, a beam of incoming light shines on a metallic surface. When the beam hits the metal, it eject electrons from the metal and sends the electrons down a tube to a collector. To do so, the light must provide the electrons with enough energy to break their bonds to the metal, and sufficient kinetic energy to reach the collector. Reaching the collector requires a certain amount of minimum kinetic energy at emission, because an electric field exists between the collector and the emitter that acts to slow down the electrons on their path. The basic set-up is shown in the figure below.

Figure 9.2.1: The Experimental Setup for the Photoelectric Effect

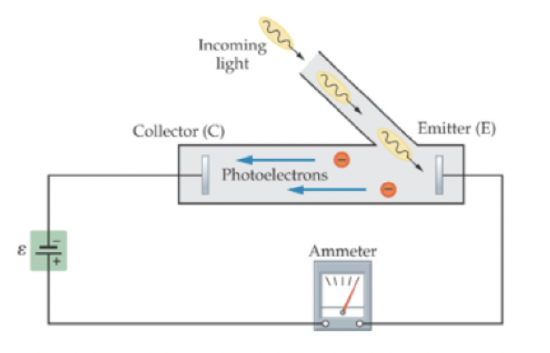
The photoelectric experiment allows us to test the wave model against the particle model, for this particular setup. As an experimenter, we have control over both the intensity of the light and the frequency of the light. We can independently vary one or the other, and note the effect, enabling us to determine the appropriate model for this system.

The photoelectric effect can be explained using the conservation of energy. Light brings in a certain amount of energy. If the energy is sufficiently high, it frees an electron from the metal. Different metals bind the electrons with different amounts of energy. If the incident light has less energy than the this binding energy, the electrons remain attached to the plate. In addition, the experiment was able to measure the amount of energy that the ejected electrons had.

Scientists who carried out these experiments observed the following properties:

• Higher intensity beams free more electrons.
• Higher frequency beams result in electrons with higher speeds.
• Changing the beam intensity has no effect on electron speed.
• Changing the frequency of the beam has no effect on the number of electrons freed (provided the frequency is high enough that some electrons are freed).

These results all support the particle model of light for the following reasons. It was postulated that beams with higher intensities contain more quanta of light, known as photons. As a result higher intensity beams free more electrons, because more photons are present to transfer energy. However, the amount of energy one photon can transfer to an electron is determined by the photon's frequency. Increasing the frequency of incoming light increases the energy transferred to the electrons, which is why higher frequency beams produce electrons with more kinetic energy. Thus, it was postulated that the energy of an individual photon depends on its frequency the following way:

\[E_{\text{photon}} = h f=\dfrac{hc}{\lambda}\label{Ephoton}\]

where \(h= 6.636 \times 10^{-34} \text{ J s}\) is Planck's constant, and \(c=3.0\times 10^8 m/s\) is the speed of light in a vacuum.Frequency is what determines the type of light we're discussing, whether it different colors in the visible range, a radio wave, or an X-ray. The photons of different colors or different types of light have different frequencies and therefore have different energies. At a particular frequency, one photon is the smallest amount of light that can exist. 

To consider the implications of the particle model, it is helpful to think about monochromatic light, many photons all with the same frequency, like light produced by a laser. We consider two properties of the light: intensity (i.e. brightness) and the amount of energy the light is able to transfer into another system, like an electron orbiting a nucleus. Returning to the photoelectric effect, compare two beams of light with equal intensity, but different frequencies. From our relationship for the energy of a photon in Equation \ref{Ephoton}, we conclude that the beam with the higher frequency has photons with higher energy. Thus, the high frequency beam is capable of transferring larger amounts energy into another system. But if the intensities of the beams are same, the total energy transferred by each beam is the same. This tells us that the beam with the higher frequency has fewer photons. But in the wave model, the same intensity of each beam means they must have the same amplitude. The energy in a wave is related to its amplitude, so it would seem both light beams must have equal ability to transfer energy. Clearly, the two models lead to different hypotheses.

Next, consider the action of increasing the beam's intensity. In the particle model, we would describe this as adding more photons to the beam, but each particular photon still only carries a certain amount of energy. Thus, more electrons are ejected, but each ejected electron still has the same kinetic energy. Using the particle model, we conclude that the brightness of the beam does not influence how much energy any particular photon can transfer to another system. In the wave model, a greater brightness would indicate a larger amplitude wave; we would conclude that greater intensity waves have the ability to transfer larger amounts of energy into another system. Again, the models make different predictions.

Electromagnetic Spectrum

We just concluded that each photon is an indivisible quantum of light, but photons of different frequencies contain different amounts of energy. So the smallest amount of energy in light is different for each type of light. The light that we experience every day is made up of many photons in a range of frequencies, so we don’t notice the quantized nature of light any more than we notice the individual atoms in everyday materials.

In fact, we categorize light of different frequencies into groups due to its various properties that arise.  Below is an image of the electromagnetic spectrum (the meaning of this term will become more useful in later chapters). As we will explore in greater detail in later chapters, the sources of electromagnetic waves (i.e. light) are oscillating electric charges. The frequency with which charges oscillate up and down sets the frequency of the electromagnetic waves produced, like similar to how the frequency of the wave on a string is set by a person at the end of the string, oscillating it.

Figure 9.2.2: Electromagnetic Spectrum of Light

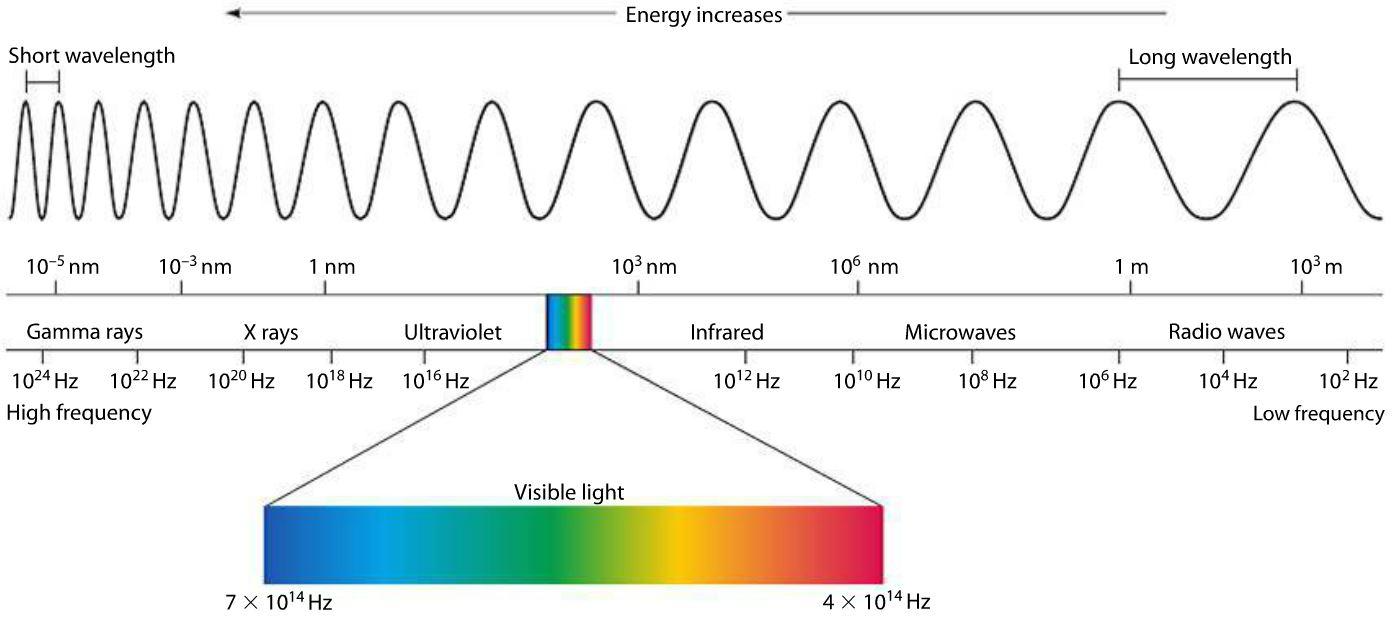
For electromagnetic waves, like all the other waves we have studied, the frequency is determined by the source. This seems a little odd, however. Most of us have been zapped by a sweater we were wearing at some point in our lives, due to the build-up of charge on it. By swaying backwards and forwards we were making those charges oscillate, but we did not seem to suddenly create light. In Physics 7A we learned that atoms at temperatures higher than absolute zero oscillated, and these atoms are made up of electrons and protons, yet most objects do not appear to glow in the dark. In fact, it seems if light is the oscillation of charge it should be very difficult to find darkness at all.

In fact we do give off electromagnetic radiation as we sway back and forth, and objects in dark rooms do "glow". Except the light created in these circumstances is not visible light. For visible light the charges have to be oscillating back-and-forth around 10¹⁴ times per second. For objects at room temperature (around 300K) the oscillating atoms give off electromagnetic light at roughly 10¹³ Hz. This light is called infrared, because its frequency is closest to red in visible light. While people cannot see this light, some animals can and we can make cameras that can detect this light. For example night-vision goggles operate by detecting infrared light as shown in Figure 9.2.2. If we want an object to give off a significant amount of visible light, we must make its atoms vibrate faster. As we learned in 7A, one way to do this is to increase the temperature. A wood fire, for example, burns at around 1500K. While most of the light is let off in the infrared, enough is let off in the visible range such that the flames can be seen. The night sky that we see is full of electromagnetic radiation with a frequency of \(3 \times 10^{11} \text{ Hz}\) which we cannot see directly. Just like infrared light, we have devices that can detect this light, and studying it gives us further insights into the origin of the universe.

Different frequencies of electromagnetic waves can be used for very different purposes. At the lowest frequencies, or at the longest wavelengths, we have radio waves as seen in Figure 9.2.2. This is a broad range of frequencies lower than roughly \(10^9 \text{ Hz}\). Most of our television and radio programs are broadcast at this frequency. At higher frequencies, there are microwaves, which are used in RADAR and microwave ovens. Above \(10^{11} \text{ Hz}\) we have the infrared, which is the light given off most strongly by objects in the temperature between 3 K and 5000 K. The “narrow” range between \(4 \times 10^{14} \text{ Hz}\) and \(7.5 \times 10^{14} \text{ Hz}\) corresponds the spectrum of visible light. In this range, different frequencies correspond to different colors of light that we can see, red in the lower frequency (longer wavelength) and blue in the higher frequency (shorter wavelength) end of the visible range spectrum.

At even higher frequencies we find ultraviolet light (UV). This region covers frequencies from \(8.6 \times 10^{14}\) to \(3.75 \times 10^{16} \text{ Hz}\) and is further broken down into the categories UVA, UVB, UVC, Far UV, and Extreme UV. UV light can be damaging to the skin (UV light given off by the sun is the cause of sunburns). The risk of damage increases with the frequency of the UV light. The sun emits radiation in the UVA, UVB, and UVC sub-bands, however almost all of the UVB and UVC radiation from the sun is absorbed in the Earth’s ozone layer in the upper atmosphere.

The use of the term X-ray varies a little. Some people take the definition of an X-ray as the manner in which the light is produced, such as an atomic transition. Others take X-ray to describe a frequency range, like our previous definitions (this latter set tend to be astronomers talking about “X-ray telescopes”). The definition is actually fairly irrelevant, except where extra clarity is needed. Whichever definition we use, it is accepted that X-rays have very high frequencies (greater than \(3.75 \times 10^{16} \text{ Hz}\)) and are energetic enough to pass through tissue. Hence we use X-ray machines to image the bones.

Gamma rays are produced in nuclear transitions, and refer to frequencies higher than 10²² Hz. Because of the quantized nature of light, when discussing gamma rays it's usually more convenient to talk about individual photons than to talk about a continuous wave. For this reason the term "gamma particles" is sometimes used interchangeably with "gamma rays".

Table 1 gives typical approximations for the order of magnitudes of wavelengths from each part of the spectrum. Because wavelength depends on medium, note that he wavelengths presented here are only valid in a vacuum.

Table 1: Order of magnitudes of Spectral Regions

Piece of the Spectrum	Typical Wavelength Size in Vacuum
Shortwave Radio	\(\lambda \sim\) Buildings
AM Radio, FM Radio, TV Broadcast	\(\lambda \sim\) People
Microwaves	\(\lambda \sim\) Insects
Infrared	\(\lambda \sim\) Fleas
Visible	\(\lambda \sim\) Cells
Ultraviolet	\(\lambda \sim\) Molecules
X-rays	\(\lambda \sim\) Atoms
\(\gamma\)-rays	\(\lambda \sim\) Atomic Nuclei

Table 2 below gives the frequencies and wavelengths of different sections of the visible light spectrum (different colors). The wavelengths presented here are only correct in vacuum, but the frequencies are correct in any medium (because frequency is set by the source of the light).

Table 2: Spectrum of Visible Light

Color	\(\lambda\) range (nm)	\(\lambda\) midpoint (nm)	Frequency (10^14Hz)
Red	620-750	700	4.3
Orange	590-620	600	5.0
Yellow	570-590	580	5.1
Green	495-570	540	5.5
Blue	450-495	470	6.4
Violet	380-450	400	7.5

Fire and Chemistry

We remarked that a typical wood fire has a temperature around 1500 K. Emitted frequencies of light at this temperature peak in the infrared range, with some light emitted in the red visible range as well. At low temperature, objects that give off light because of thermal energy (e.g. hot metal) glow a dull red. As the temperature increases, the peak of emitted frequencies becomes higher, and some blue light starts to appear. The dull red becomes an orange as higher frequencies become emitted, and eventually the orange becomes white, which contains many frequencies. The range of frequencies emitted also increases as the temperature goes up, so the light always contains some amount of red in it. We do not observe objects so hot that only glow blue – there is always some contamination from the lower (red) part of the spectrum.

When you study chemistry, you will observe that burning different metals (e.g. in a Bunsen burner) produces different colors of flames. If you have not seen this in chemistry you have probably seen it in a fireworks show – various chemicals in the fireworks give off different colors when they oxidize. This seems to contradict our previous statement that hotter objects glow at different frequencies, but retain red in their emitted light. However, the light we mentioned here is not really thermal light. Thermal light is due to the random motion of charges and the equipartition of energy. The light given off by fireworks is different colors because oxidizing pure substances gives off light whose frequency is determined by the energy available to electrons in the metal. The effect is quantum mechanical, not thermal. We discuss this effect more when we talk about photons and the energy spectrum available to a system.

Which Model is "Correct"?

At this point, you might wonder which model is the “correct” model of light. The answer is neither. In more sophisticated treatments physicists have developed a “quantum model” to explain light, which incorporates all the examples we have discussed so far. However, we should refrain from saying that light is actually this quantum stuff, because future experiments may require us to replace this model with something else.

If neither model of light is correct, why do we teach them? Ultimately the full quantum model is beyond the scope of this course. Furthermore, we can answer many questions about light by using the particle model or the wave model of light; both of these simpler models correctly capture aspects of light’s behavior. Many books perpetrate confusion by claiming that light is somehow “both a particle and a wave". We have a good quantum model for light (and electrons, and even whole atoms): in some situations we can simplify this and use the wave model, while in others we can use the particle model. In other situations the quantum model does not fit into either a wave or particle description. Light and other microscopic phenomena often behave in unfamiliar ways completely outside human experience. Even if we cannot shoehorn quantum mechanics into our regular familiar notions of "particles" and "waves," this does not mean quantum mechanics is contradictory, it just means that the microscopic world is highly counter-intuitive.

Because the wave-particle “duality” or “contradiction” is bought up so often, it bears repeating. Light can be modeled as particles when it behaves as such and it can be modeled as a wave likewise. We use these models when more complicated behaviors of light can be ignored or simplified, and we recognize that each model has limits and only applies under specific conditions.