9.3: Energy Quantization

Matter Waves

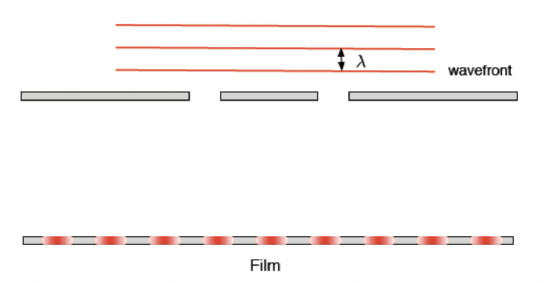
Our definition for a wave has been limited so far, we referred to (material) waves as oscillations of a medium about its equilibrium position in time and space. Light waves light are oscillations in the electromagnetic fields which do no require a medium to propagate. In addition, in the previous section we discussed the validity of a particle model of light. Let us momentarily refer to light as a wave because it obeys the principle of superposition. Superposition gives rise to constructive and destructive interference; an example of this is two-slit interference. Light of a given frequency, going through two narrow slits, superposes to give rise to the bright and dark bands as shown in the figure below.

Figure 9.3.1: Double-Slit Interference of Light

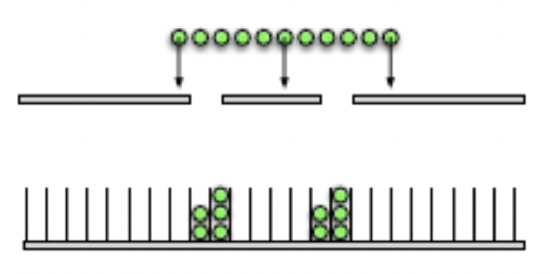
On the other hand, particles cannot interfere like this, they travel through slits one at a time. The figure below shows the pattern particles would make.

Figure 9.3.2: Particle Double-Slit Experiment

What would electrons do if they were also passed through two slits? Since we are used to thinking of electrons as individual particles, we may expect a particle-like interference pattern like the one pictured above, with two bright spots right across the two slits. However, what is actually observed when electrons are sent through a two-slit set up, we get quite an unexpected result – the electrons form an interference pattern similar to waves as pictured below.

Figure 9.3.3: Electron Double-Slit Experiment

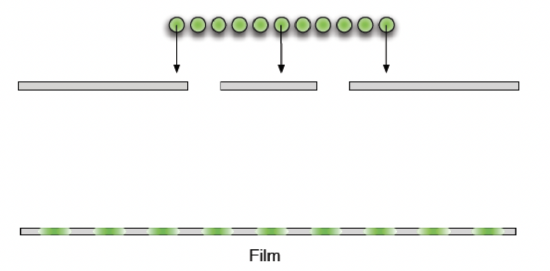
In fact, the interference pattern created by the electrons is identical to one created by light with a wavelength given by:

\[\lambda=\dfrac{h}{p}\approx \dfrac{h}{mv}\]

and with the same phase difference between the two slits. The approximation above is valid if \(v\ll c\). The wavelength, \(\lambda\), associated with particle waves is called the de Broglie wavelength, named after a French physicist Louis de Broglie who made significant contributions to the development of quantum mechanics. Just as light can exhibit particle-like properties (such as in the photoelectric effect), matter can exhibit wave like effects (such as electron interference patterns).

Particle Energy Levels

Until this unit, our model of energy allowed a particle to have any value of energy. In the quantum mechanics model, this is still true for particles moving freely through space, but the energy of a confined particle is quantized – meaning only certain values of energy are allowed. Like with other models, understanding a few key ideas about quantized energy levels will enable us to make sense of a variety of phenomena, from the emission spectrum of the hydrogen atom to the unfreezing of modes in vibrating atoms. This is analogies to the allowed frequencies for classical waves. If a wave is generated in a continues medium (such as an infinite string), then you can oscillate it with any frequency to produce the wave. However, when the medium is confined (such as a string tied at both ends), then only a discrete (quantized) number of frequencies of waves can be generated on this medium, as described by standing waves. Similarly, in quantum mechanics when the particle is bounded by some potential (such as an electron bound by the atomic nucleus), then matter standing waves are generated which restrict the allowed frequencies, and thus energies, of the particle.

When we describe the energy of a particle as quantized, we mean that only certain values of energy are allowed. Perhaps a particle can only have 1 Joule, 4 Joules, 9 Joules, or 16 Joules of energy. In this case, whenever we measure the particle’s energy, we will find one of those values. If the particle is measured to have 4 Joules of energy, we also know how much energy the particle can gain or lose. It can only gain the exact amount of energy needed to reach one of the higher energy levels, and it can only lose the exact amount of energy needed to reach a lower energy level. In this case, the particle with 4 Joules of energy can gain either 5 Joules (to reach the 9 J level) or 12 Joules (to reach the 16 J level). No other amount of energy could be added to the particle (unless there were more available energy levels). Similarly, the only lower energy state is 1 J, so if the particle lost energy, it could only lose exactly 3 Joules. The available energy state with the least amount of energy is called the ground state. Any higher energy levels are called excited states. The next highest state after the ground state is called the first excited state, followed by the second excited state, and so on.

How does a particle change its energy level? If a particle goes to a higher energy level, it must have gained that energy from another system. Likewise, if a particle goes to a lower energy level, that energy must be transferred into another system. We know that energy is conserved if we consider all systems involved in the process of energy transfer. So what systems gain or lose energy to our particles? The most common systems that accept and give energy to systems of small particles are electromagnetic waves (light) and the vibrations of molecules (heat or sound). We will talk about the energy of light in more detail below.

The collection of allowed energies a system may have is called the energy spectrum of that system. The levels in the spectrum tell us the total energy the particle is allowed. Typically, the total energy is the sum of the kinetic and potential energies. The energies that a system is allowed to have depend on the potential energy of the system. We call potential energy \(PE(r)\) because we typically explore circumstances where \(PE\) depends on one variable \(r\). In effect, the potential energy forms a “container” of sorts that confines the particle to a specific range of \(r\). Each unique container has its own set of energy levels. We explore the different spectra of different \(PE\) "containers" in the following sections.

As discussed earlier, the exact potential energy of a particle is not important, but the changes in potential energy really matter. In quantum mechanics, this is still the case. In effect, we can set "zero" potential energy to be at any level, so in our examples we will establish conventions that make interpreting the results as simple as possible.

Energy Level Transitions

There are multiple ways that a particle whose energy is quantized can change its energy levels, but we will focus on one specific processes depicted below. The figure below depicts arbitrary energy levels for some particle, known as the energy spectrum. The horizontal lines represent the quantized energy levels with increasing values upward. The spacing between the lines shows the energy differences between consecutive levels. In this example the energy levels get closer together as the energy increases. In the following sections we will see examples of different types of energy spectra which is determined by the type of potential by which the particle is confined. 

Figure 9.3.4: Energy Level Transitions

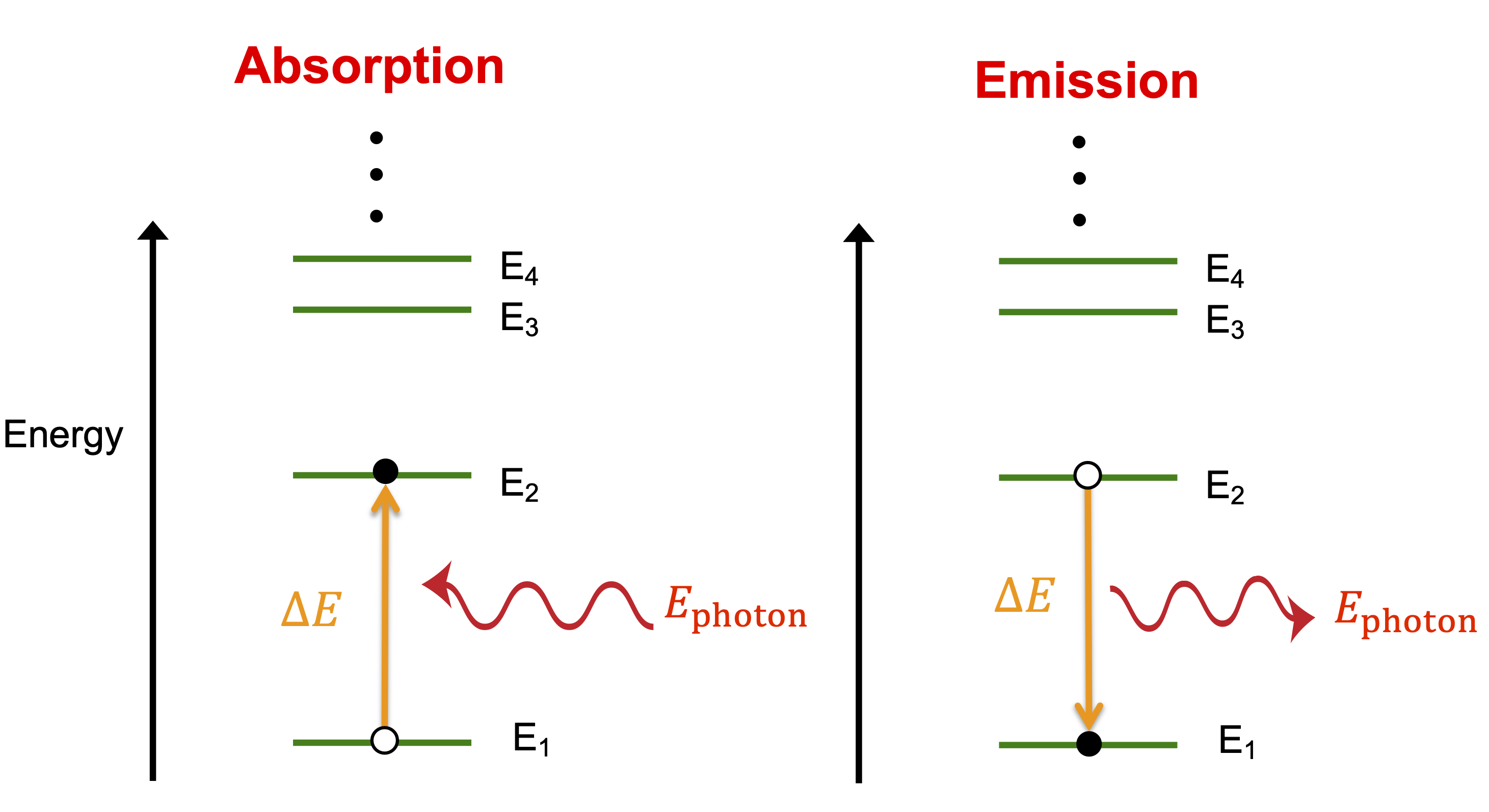
A particle can increase its energy by getting the needed energy from a photon. In the process known as absorption, a particle absorbs a photon which provides it the extra energy needed to increase to a higher energy level. Since the energy levels are quantized, the energy of the photon has to be exactly equals to the energy difference, \(\Delta E\), between two levels. In the figure above the particle is making a transition for its ground state, \(E_1\), to the next higher energy level, \(E_2\). For the transition to be possible the energy of the photon, \(E_{\text{photon}}\) has to be equals to \(E_2-E_1\). If the photon energy is a little lower or a little higher, the photon will not be absorbed by this particle. The photon's energy is indivisible, so the particle cannot partially absorb the photon. If the incoming photon's energy is equal to the energy difference between the first and the third level, then upon absoption, the particle would transition to the third energy level. Generally, this can be written as:

\[\Delta E=E_{\text{photon}}=hf=\dfrac{hc}{\lambda}\] 

Since wavelengths of light are often very short, we frequently use the units of nanometer for wavelengths of light: \(1 nm=1\times10^{-9}m\). This give rise to another useful way to calculate \(hc\) in the equation above:

\[hc=1240~\text{eV}\cdot\text{nm}\]

You can use the units above as long as \(\lambda\) is in units of \(nm\). The resulting energy will be in units of electron volts, eV. The energy unit "eV" is related to Joules in the following way:

\[1 \text{eV}=1.6\times 10^{-19} J\]

Similarly, when a particles drops from a higher to a lower energy level, that change in energy is conserved by a creation of a photon due to the transition. This is known as photom emission. This process is depicted above for a particle dropping from a higher energy level, \(E_2\), to a lower energy level, \(E_1\), and as a result emitting a photon whose energy must equal exactly the energy difference between the two levels, \(E_2-E_1=E_{\text{photon}}\). Even though the final state is the lower energy one, the energy of a photon is always positive, so you still subtract the lower energy from the higher one even when the photon is being emitted and the energy difference between energy levels is negative.